13. Поверхностнофильтрационная.

Схема явления.

Явление капиллярности – подъем или опускание уровня жидкости под действием так называемых сил поверхностного натяжения – известно давно. Дополнительное давление жидкости, возникающее под ее искривленной поверхностью, определяется формулой Лапласа (1806)

р = [(1/r₁) + (1/r₂)] н/м², (530)

где  - коэффициент поверхностного натяжения, н/м;

r₁ и r₂ - радиусы кривизны поверхности в двух взаимно перпендикулярных направлениях, м.

Парциальное давление пара р_п над искривленной поверхностью связано со скоростью испарения жидкости из капилляра формулой Стефана (1182)

J_m = [(Dр_б)/(RTh)]ln[(р_б – р_с)/(р_б - р_п)] кг/(м²сек) (531)

где D - коэффициент диффузии;

 - молекулярная масса;

р_б - общее барометрическое давление воздуха;

р_с - парциальное давление пара в окружающей среде;

R - газовая постоянная;

h - расстояние от края капилляра до мениска жидкости в нем.

Согласно общей теории, частные эффекты капиллярности (530) и испарения жидкости (531) входят в состав общего явления поверхностнофильтрационной пары, которая функционирует под действием разности значений поверхностного интенсиала (рис. 26) [11, 14, 16]

_п = _п” - _п’ дж/кг. (532)

Фактически имеются две различные пары – одна образована пристеночным и осевым слоями жидкости (рис. 26-б и 26-в), а вторая – жидкостью мениска и паром, соприкасающимся с мениском (рис. 26-г).

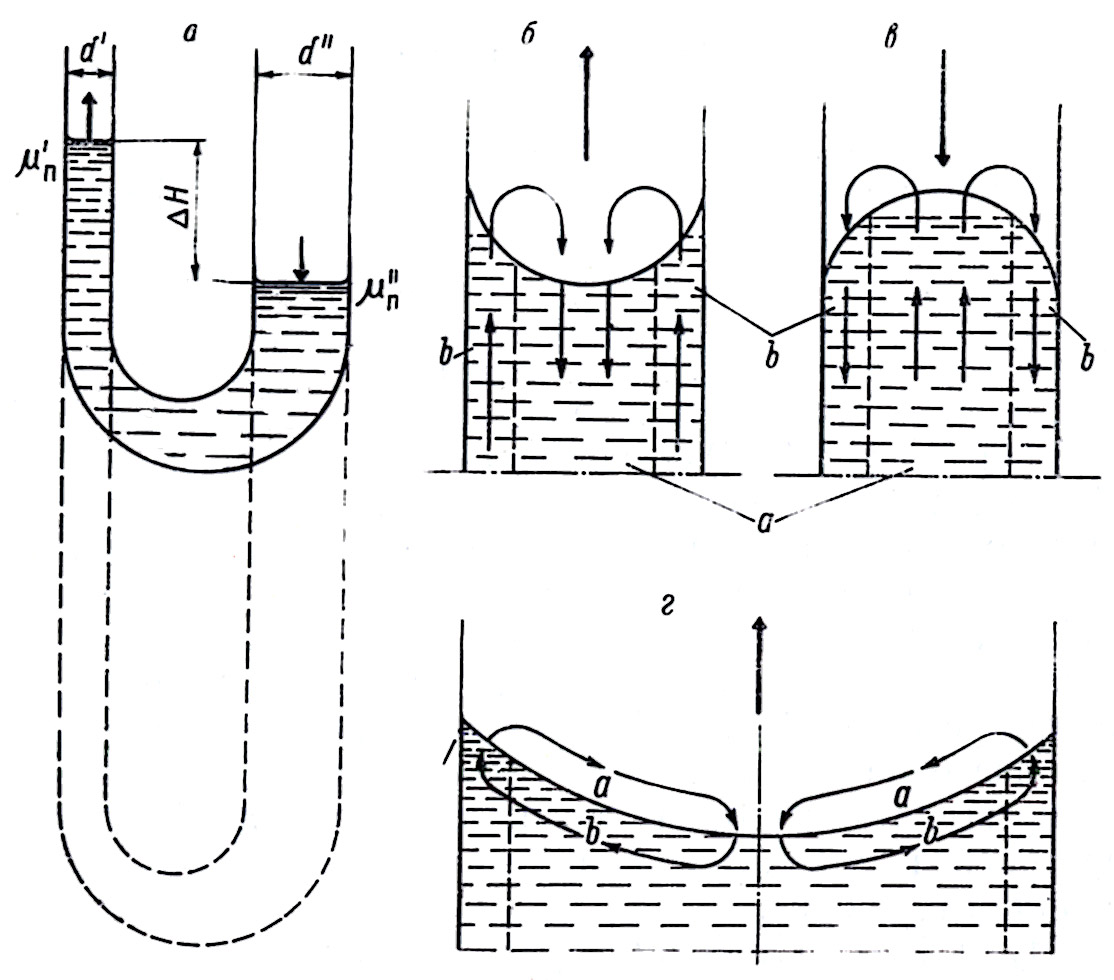
Рис. 26. Схемы поверхностнофильтрационной пары (а)

и варианты циркуляции жидкости и пара в капилляре

(б - смачивание, в – несмачивание) и вблизи мениска (г).

Вторая пара весьма интересна. Одна ее ветвь – пар, а вторая – жидкость в поверхностном слое мениска. Спаями пары служат внешний контур мениска и осевая часть поверхности. При смачивании циркуляция происходит благодаря испарению жидкости на пристеночном и конденсации пара на осевом участке мениска. При несмачивании циркуляция имеет обратное направление. Эта циркуляция представляет собой любопытный пример вечного в целом бездиссипативного макроскопического движения жидкости и пара в условиях, если система полностью изолирована от окружающей среды.

Анализ явления.

Поверхностнофильтрационная пара подчиняется законам § 6 и 7 и проявляет все положенные ей эффекты. Анализ с позиции теории термодинамической пары соотношений (530) и (531) позволяет выяснить их истинный физический смысл и установить границы применимости.

Например, давление р в формуле (530) Лапласа соответствует фиктивной движущей силе р_с в уравнениях (484) – (486). Выражения (486) и (530) совместно определяют физический смысл коэффициента поверхностного натяжения.

Согласно формуле (530), при стремлении радиуса капилляра к нулю дополнительное давление р возрастает до бесконечности. На самом деле при r₁ = r₂  0 величина р = р_с стремится к некоторому конечному максимальному значению, определяемому условием (527). Иными словами, дополнительное капиллярное давление (высота Н подъема жидкости – рис. 26) не может превышать того, которое соответствует d  2₀. Этот вывод-прогноз поддается сравнительно несложной экспериментальной проверке.

Формула (531) Стефана характеризует процесс испарения жидкости из капилляра. В этой формуле парциальное давление р_п имеет весьма условный смысл: над мениском происходит сложная термодинамическая циркуляция пара, так как его давление над пристеночным и осевым участками поверхности не одинаково. Поэтому формулой (531) можно пользоваться, если под р_п понимать некоторую осредненную величину, определяемую законами термодинамической пары.

Более подробный теоретический и экспериментальный анализ формулы Стефана приводится в работе [11] и сборнике [15]. Процесс испарения жидкости из капилляров и со свободной (плоской) поверхности при наличии многих степеней свободы рассматривается также в предыдущих работах автора [11, 16].

Перенос пара от мениска в окружающую среду при испарении жидкости из капилляра нарушает процесс функционирования поверхностнофильтрационной пары. Это влияет на величину р_с, что подтверждается опытом. Кроме того, наличие тепловых контактных эффектов на поверхности мениска капилляра изменяет (уменьшает) теплоту парообразования по сравнению со свободной поверхностью. Это было подтверждено в опытах с водой, бензолом, спиртом и т.д. При прочих равных условиях скорость испарения из капилляров значительно выше, чем со свободной поверхности.

Поверхностнофильтрационные пары широко используются на практике (действие фитилей, пропитка древесины, устранение пористости в отливках, флотация руд и т.д.) и играют важную роль в природе.