6. Теория обобщенной пары.

Схемы действия пар.

Теперь мы вполне вооружены для того, чтобы приступить к описанию и анализу свойств термодинамической пары. Как уже отмечалось, явление термодинамической пары входит в качестве самостоятельной составной части в общую качественную классификацию астаты. Это явление еще удается изучить достаточно подробно и указать основные специфические законы, которым оно подчиняется. За парой классификация астаты содержит пропуски, о которых пока ничего определенного сказать нельзя. Явление термодинамической пары весьма универсально. Природа использует его в живых организмах для транспорта питательных веществ, для процессов обмена и т.д. Оно находит также применение в технике. Общая теория пары была описана в работах [8, 10, 11, 14]. Суть явления термодинамической пары заключается в следующем.

Если, например, при n = 2, соединить концами два родственных проводника а и б и создать между спаями (на рис. 15 зачернены) разность первого интенсиала

Р₁ = Р₁^” - Р₁^’, (459)

то в полученной таким образом цепи возникнут многочисленные эффекты. В частности, в спаях образуются неодинаковые скачки второго интенсиала, вызывающие круговую циркуляцию второго экстенсора, интенсивность которой определяется разностью значений первого интенсиала. В ветвях пары наблюдаются так называемые линейные эффекты. Циркуляция второго экстенсора в спаях и ветвях сопровождается положительными и отрицательными эффектами трения (плюс- и минус-диссипация) и т.д. [8, 10, 11, 14].

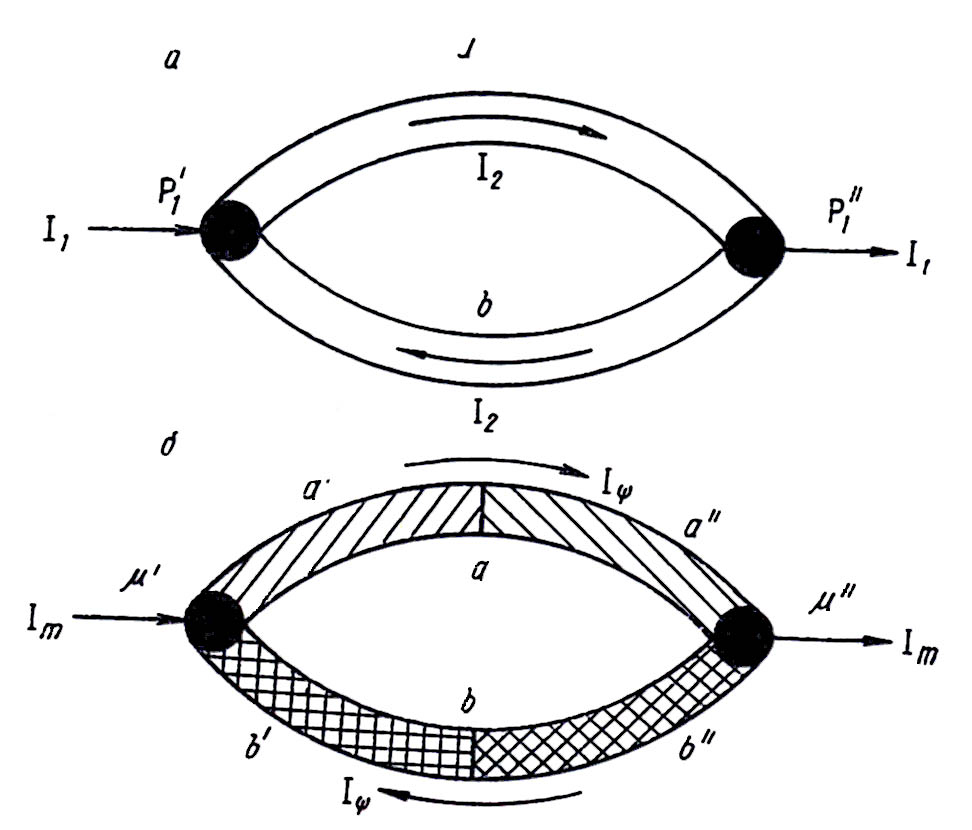
Рис. 15. Схемы соединения проводников в термодинамической паре.

Газ, жидкость или твердое тело, заполняющие капилляр – трубку с тонким отверстием, тоже представляют собой термодинамическую пару. Будем называть ее фильтрационной. Пристеночный (точнее, капиллярный) слой вещества толщиной ₀, испытывающий молекулярное взаимодействие с материалом капилляра, играет роль проводника б, осевой слой вещества, не испытывающий такого воздействия, - роль проводника а. Проводники а и б обладают неодинаковыми значениями коэффициентов А в уравнениях состояния. Спаями, т.е. местами контакта проводников а и б, служат концы капилляра.

Если между спаями создать разность некоторого интенсиала Р₁, то в цепи появятся все эффекты, присущие обычной паре, а также два новых – фиктивной движущей силы и разделения. Вторым – циркулирующим экстенсором в большинстве случаев служит само вещество, заполняющее капилляр: в пристеночном слое оно фильтруется или диффундирует в одном направлении (на рис. 16 влево), а в осевом – в другом (вправо). Таким образом, рис. 16 отражает схему круговой циркуляции вещества как в фильтрационной, так и в диффузионной паре.

Рис. 16. Схема действия фильтрационной пары.

Пристеночный слой играет роль насоса, поэтому, если на концах капилляра имеются емкости конечных размеров второго экстенсора, то происходит переток вещества из одной емкости в другую и появление между емкостями разности давлений

р_с = р_с” - р_с’ н/м². (460)

Величина р_с представляет собой фиктивную движущую силу.

Циркуляция сложного по составу вещества сопровождается эффектом разделения: концентрация отдельных компонентов смеси в разных емкостях получается неодинаковой. О количественной стороне эффекта разделения можно судить по отношению

k_р = р_с/Р₁. (461)

Капиллярнопористое тело содержит в себе большое число пор и капилляров. Поэтому в нем наблюдаются те же эффекты, что и в отдельном капилляре.

Теория пары.

На рис. 17 изображена схема обобщенной термодинамической пары, в которой места спаев обладают емкостями (резервуарами) второго экстенсора К₂^’ и К₂. В общем случае между каждой емкостью и проводниками а и б имеются свои скачки второго интенсиала. Суммарные скачки в первом и втором спаях

Р₂’ = Р_2а’ + Р_2б’ = Р_2а’ - Р_2с’ + Р_2с’ - Р_2б’ = Р_2а’ - Р_2б’; (462)

Р₂” = Р_2а” + Р_2б” = Р_2с” - Р_2а” + Р_2б” - Р_2с” = Р_2б” - Р_2а”; (463)

Фиктивная движущая сила определяется разностью

Р_2с = Р_2с” – Р_2с’. (464)

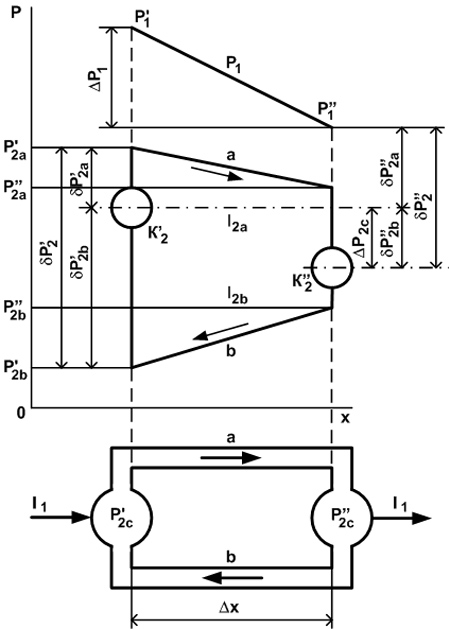
Рис. 17. Схема действия обобщенной термодинамической пары.

Обобщенная пара охватывает все основные случаи, встречающиеся на практике. В частности, она описывает фильтрационную пару (рис. 16). Если емкости К₂^’ и К₂” равны нулю, то получается пара, изображенная на рис. 15.

Рассмотрим теперь количественные соотношения, характеризующие работу обобщенной термодинамической пары. Энергию, необходимую для поддержания циркуляции второго экстенсора, поставляют среда и частично движущийся первый экстенсор. В обычных условиях главную долю энергии дают эффекты контактной и линейной диссипации (экранирования). В излагаемой ниже теории для простоты принимается, что в спаях имеются скачки только второго интенсиала. Кроме того, не учитываются некоторые эффекты второго порядка и т.д.

Суммарные контактные в спаях и линейные в проводниках работы второго экстенсора определяются выражениями [14]

dQ_2k = dQ_2д” - dQ_2д’ = Р₂”dE₂ - Р₂’dE₂ = Р_2kdE₂ дж; (465)

dQ_21л = dQ_21б - dQ_21а = Р_21бdE₂ - Р_21аdE₂ = Р_2лdE₂ дж; (466)

где

Р_2k = Р₂” - Р₂’; (467)

Р_2л = Р_21б - Р_21а. (468)

Следовательно, полезная работа циркуляции второго экстенсора

dQ₂ = dQ_2k + dQ_2л = (Р_2k + Р_2л)dE₂ = Р₂dE₂ дж, (469)

где полная движущая сила термодинамической пары

Р₂ = Р_2k + Р_2л. (470)

Контактная составляющая движущей силы Р_2k может быть выражена через разность Р₁ первого интенсиала с помощью уравнения состояния. Например, при dE₂ = 0 из уравнения (26) находим

dР₂ = (А₂₁/А₁₁) Р₁. (471)

Для тел а и б суммарная контактная движущая сила

Р_2k = Р₂” - Р₂’ = Ф₂₁Р₁, (472)

где

Ф₂₁ = (А_21б/А_11б) – (А_21а/А_11а). (473)

У идеальных тел коэффициенты А постоянны, поэтому интенсиалы Р_2а и Р_2б пропорциональны интенсиалу Р₁ и коэффициент

Ф₂₁ = d(Р_2k)/dР₁ = Р_2k/Р₁ = Р₂’/Р₁’ = Р₂”/ Р₁”. (474)

Линейная составляющая движущей силы пары Р_2л определяется несколько сложнее, чем контактная. Из всех эффектов, влияющих на Р_2л, учтем только два. Они связаны с линейным экранированием термиора ансором-носителем, который циркулирует по замкнутой цепи пары. Носитель имеет в своем составе экстенсоры Е₁ и Е₂. При его циркуляции вместе с экстенсором dE₂ преодолевает разность интенсиалов Р₁ также экстенсор dE₁. Первая работа экранирования равна произведению этих величин. Но dE₁ пропорционально dE₂, поэтому работа экранирования пропорциональна Р₁dE₂. Эта работа в соответствии с уравнением состояния изменяет все интенсиалы носителя, включая Р₂. В результате появляется дополнительная движущая сила Р_2л, преодоление которой экстенсором dE₂ сопровождается эффектом экранирования. Учитывая, что Р_2л пропорционально dE₂, окончательно найдем [16]

dQ_21л = (В_21б^’ – В_21а’)Р₁(dE₂)³ = Р_2лdE₂,

где В – коэффициент пропорциональности.

Удобнее всего оперировать секундными работами, т.е. потоками, тогда

I_Qл = (В_21б – В_21а)Р₁I₂³ = Р_2лI₂ вт (475)

и

Р_2л = (В_21б – В_21а)Р₁I₂². (476)

Линейная составляющая движущей силы пропорциональна разности интенсиалов Р₁ и квадрату потока второго экстенсора.

Следовательно, полная движущая сила термодинамической пары

Р₂/Р₁ = (Р_2к/Р₁) + (Р_2л/Р₁) = Ф₂₁ + (В_21б – В_21а)I₂². (477)

Полная движущая сила расходуется на преодоление сопротивлений цепи. Если пренебречь сопротивлениями спаев, тогда связь между движущей силой Р₂, перепадами интенсиала в проводниках а и б

Р_2а = Р_2а^” - Р_2а’; Р_2б = Р_2б^” - Р_2б’ (478)

и сопротивлениями проводников R_2a и R_2б - формула (139) – найдется с помощью выражений

Р_2а = I_2аR_2a + Р_2а; Р_2б = I_2бR_2б + Р_2б. (479)

На стационарном режиме работы пары, когда I_2а = I_2б = I₂, получаем

Р₂ = I₂(R_2a + R_2б) = Р_2а + Р_2б + Р_2л (480)

или

Р_2к = Р_2а + Р_2б. (481)

Сумма измеренных перепадов второго интенсиала вдоль проводников равна контактной составляющей движущей силы.

Под действием движущей силы Р₂ в паре происходит циркуляция второго экстенсора и появляется фиктивная движущая сила Р_2с. Для ее определения представим полную движущую силу в виде

Р₂ = Р_2а + Р_2б, (482)

где Р_2а и Р_2б - движущие силы верхнего и нижнего участков пары (над и под емкостями, рис. 17),

Р_2а = - Р_2а^’ - Р_21а + Р_2а”; Р_2б = - Р_2б^’ + Р_21б + Р_2б”. (483)

Через эти движущие силы путем несложных преобразований можно найти зависимость величины Р_2с от времени. Имеем [10, 11, 14]

Р_2с = (Р_2б – n₂Р_2а)/(1 + n₂){1 – exp[-(1/R_2a + 1/R_2б)(1/К₂’ + 1/К₂”)t]}, (484)

где

n₂ = R_2б/R_2а. (485)

Из этой формула видно, что в начальный момент (t = 0) фиктивная движущая сила равна нулю. С течением времени Р_2с растет по экспоненциальному закону. При t =  наступает стационарный режим, величина Р_2с приобретает максимальное значение

Р_2с = (Р_2б – n₂Р_2а)/(1 + n₂) (486)

В условиях стационарного режима потоки второго экстенсора в проводниках а и б одинаковы. Находим

I_2а = I_2б = (Р_2а + Р_2с)/R_2а = (Р_2б - Р_2с)/R_2б =

+ (Р_2а + Р_2б)/(R_2а + R_2б) = Р₂/(R_2а + R_2б) (487)

Необходимо подчеркнуть, что величина Р_2с не есть движущая сила процесса циркуляции второго экстенсора, как иногда думают. Фактической движущей силой служит разность Р₂. Исходной причиной функционирования пары являются связи, заключенные в уравнениях состояния. Любая термодинамическая пара представляет собой преобразователь, в котором под действием экранированного термиора происходят взаимные превращения активностей различных элат.