4.Отбор факториальных признаков в множественных регрессионных моделях, без учета временного лага Этапы решения задачи для размерных регрессионных моделей без учета временного лага.

1. Отбор фиксированных признаков.

   0. На основание экономического анализа производится первоначальный отбор факториальных признаков.

Пример:

Пусть y_t - цена на выпускаемую продукцию.

Выявляем от чего зависит цена:

x₁ =t (настоящее время),

x₂ –стоимость (цена) сырья,

x₃ – с/с выпускаемой продукции,

x₄ –выпуск продукции,

x₅ –курс валюты,

x₆ –капиталовложения в производство.

0. Выявление факториальных признаков оказывающих достаточно сильное влияние.

С этой целью рассчитываются коэффициенты корреляции между y и каждым из факториальным признаков:

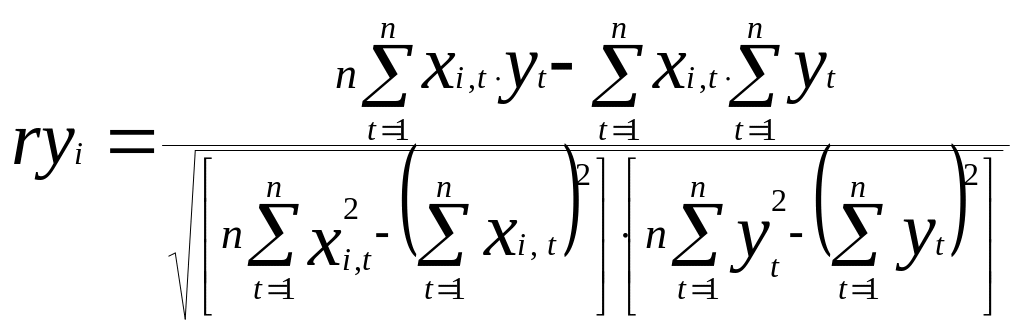
Коэффициенты корреляции характеризуют тесноту связи между двумя исследуемыми показателями. По модулю всегда ry_i ≤ 1. Чем больше модуль, тем более тесная связь, чем меньше, тем меньше связь.

ry_i = ±1 означает функциональную зависимость,

ry_i = 0 полную независимость,

ry_i > 0 означает возрастание зависимости одного от другого,

ry_i < 0 означает убывание.

Если полученное значение

| ry_i | < ry_кр =0,2,

то х_i оказывает слишком маленькое влияние на исследуемый показатель и должен быть отброшен из рассмотрения.

Обозначим p – сколько осталось факториальных признаков. Полученные х уплотним.

0. Отброс сильно коррелирующих факториальных признаков.

Расчет коэффициентов корреляции между самими факториальными признаками.

Обозначим ry_i,j – коэффициент между i и j корреляционными признаками.

Если полученный коэффициент корреляции |ry_i,j| > ry_кр =0,8, то один из них i-ый или j-ый будет отброшен.

Возможны следующие варианты отброса i-ого или j-ого показателя:

1. математический (отбрасываем тот, у которого коэффициент корреляции меньше);

2. экономический;

3. комбинация а) и b) с учетом других коэффициентов корреляции.

Обозначим p – новое количество оставленных факториальных признаков.

Отброс сильно коррелируемых факторных признаков необходим для исключения двойного влияния их, а также для придания устойчивости модели.

Рассмотрим пример: даны y, x₁, x₂ так, что коэффициенты корреляции между x₁ и x₂ равен 1.

y	x1	x2
7	2	5
10	3	7
22	7	15
28	9	19

x₂ =2x₁+1, y = x₁ + x₂;

rх_1,2 =1;

Зависимость y = x₁ + x₂ можно также переписать в виде:

y = 3x₁ + 1 или y = x₂ + (x₂ - 1)/2.

y = αx₁ + βx₂ так, что α и β связаны между собой.

Если при таких данных пытаться строить регрессионную модель, то определитель матрицы системы уравнений окажется равным нулю, что и соответствует бесконечному количеству решений.

Если зависимость не чисто функциональная, а коэффициент корреляции больше критического и близок к единицы, то определитель системы окажется близок к нулю. И полученное решение системы будет не устойчиво и не пригодным для использования.

2. Расчет коэффициентов регрессии.

Линейная модель имеет вид:

Для общности введем дополнительную переменную x_p+1=1.

Тогда

Введем функцию:

,

t – номер эксперимента(замера).

Ищем производную

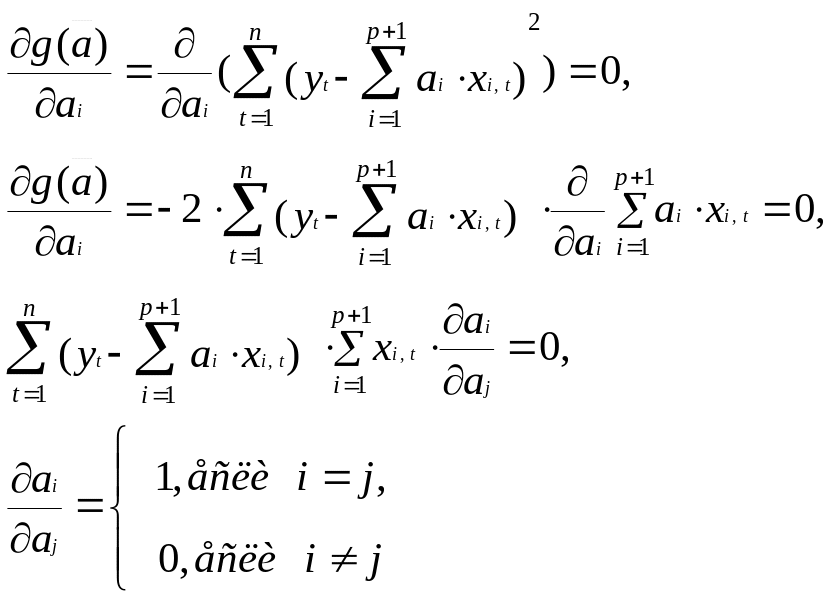
Следовательно в третьей сумме отличен от нуля только член, в котором i=j.

Меняем порядок суммирования и вынесем а_i за знак внутренней суммы. Получается:

, где D_i,j и C_j - числа.

Следовательно, полученная линейная система состоит из (p+1) уравнения и с (p+1) неизвестными.

Система симметрична:

D_i,j = D_j,i

Если по одной или несколько переменным зависимость нелинейна, то можно ввести одну или несколько новых переменных, включающих в себя нелинейную часть.

3. Проверка адекватности.

Осуществляется по критерию Фишера, рассчитываются δ²_{фак ,} δ²_ост.

(n-p-1) – кол-во степеней свободы.

F_ст с выбранной вероятностью (0,95) и кол-вом степеней свободы

k₁ = p, k₂ = n - p -1.

Если F_кр>F_ст , то модель адекватна с выбранной доверительной вероятностью.

На лабораторной работе на график y_t(t) нанести и сопоставить. В силу того, что присутствует временной лаг на графике возможно смещение.

Если модель оказалась не адекватна то можно попытаться включить либо какие-то другие неучтенные параметры, либо, если модель связана со временем, использовать модель учитывающую временной лаг.

3. Прогнозирование.

Осуществляется с подстановкой факториальных признаков х_i в полученную модель

(1)

При этом возможны два принципиально разных варианта:

0. t не является параметром времени, а является номером эксперимента. В этом случае модель не временная и значение параметров х_i для подстановки в формулу 1 определяется в зависимости от требований.

1. t является параметром времени. В этом случае вместо него подставляется t = n+1, n+2…

Для получения х_i нужно использовать их прогнозное значение.

При этом возможно следующие:

для некоторых х_i построить временную регрессионную модель (можно использовать одиночные временные ряды(курс доллара), сезонные колебания модели(выпуск продукции), адаптивные модели, а также авторегрессионные модели), а для некоторых использовать прогнозные значения на основание эвристического или экономического анализа. При этом следует иметь ввиду, что нельзя использовать для всех факториальных признаков только временные модели, иначе это было бы равносильно тому что

Реально возможна многовариантность!

Замечание: По аналогии с методом исследования одиночных временных рядов необходимо(желательно) выполнение условия: кол-во параметров p+1 ≤ n/4 . Это условие является условием устойчивости системы линейных уравнений и оно должно быть выполнено по завершению отбора факториальных признаков.

Если оно все же не выполнено, то необходимо дополнительные исследования устойчивости системы линейных уравнений с помощью определителя с учетом значений самих коэффициентов.

Достоинством рассмотренной регрессионной модели является ее простота прогнозирования.

Недостатком является:

1. найденные коэффициенты регрессии a_i размерные и, следовательно, их значение существенно зависит от единицы измерения (показать),

2. как следствие п.1(из-за размерности), невозможно произвести сопоставление относительной значимости этих коэффициентов.