2. Укрупненный алгоритм оцкп для 3-х факторов (подробно о проверке воспроизводимости и значимости коэффициентов)

Число опытов и величина a в ОЦКП
Характеристика плана	Число факторов
	2	3	4	5	6	7
«Ядро» плана	22	23	24	25–1	26–1	27–1
Число дополнительных точек (2k+1)	5	7	9	11	13	15
Общее число опытов N	9	15	25	27	45	79
Величина a	1,00	1,215	1,414	1,547	1,721	1,955

Для оптимизации процесса в окрестности экстремальной точки широко используется модели в виде полинома 2-го порядка:

Для получения модели эксперимент проводят на трех уровнях, т.е. с N=3ⁿ, что нерационально и переходят к ЦКП включающему:

1. точки ПФЭ с N_ф =2ⁿ при n<5

или ДФЭ с N_ф =2^n-1 при n>5

2. звездные точки плана типа креста c N_ =2n с расстоянием  от центра плана (-звездное плечо)

3. нулевые точки N0

Т.о. N=N_ф+N_+N₀ и для n=2 и N₀=1, N=9

Для получения оценок коэфф. влияния независимо друг от друга необходимо выполнение условия ортогональности плана, определяющие равенство 0 суммы элементов столбцов матрицы планирования

Ортогонализация столбцов Z0 и Zi² производится с помощью преобразования:

т.е. сумма отклонений от среднего должна быть равна нулю как и в других столбцах. Тогда из условий ортогональности

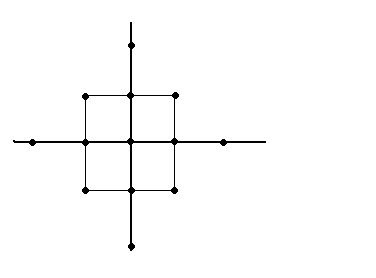
выводится уравнение для расчета звездного плеча 

4⁴+4 N_ф²- N_ф(N_+ N₀)=0

Исходя из ортогональной матрицы с преобразованными столбцами для квадратичных эффектов модель процесса вида:

; i=1,n

Оценка значимости коэффициентов производится по критерию Стьюдента:

; =(-1)*N

Если t > tкр , то коэффициент принимается значимым и число значимых коэффициентов q увеличивается на 1, т.е. q=q+1; в противном случае bi=0 оценка принимается равной нулю.

Далее следует оценка адекватности найденного уравнения регрессии по критерию Фишера:

; 1=N-q; 2=N(m-1)

где

-дисперсия адекватности

- расчетные значения Yk,

вычисленные по найденному уравнению регрессии.

Общий алгоритм нахождения уравнения регрессии с квадратичными эффектами включает в себя следующие этапы:

1. Ввод матрицы ЦКП и проверка воспроизводимости опытов с m повторений (Кохрен).

2. Вычисление коэффициентов регрессии и проверка их значимости по Стьюденту;

3. Проверка адекватности найденного уравнения по критерию Фишера с распечаткой таблицы расчетных и экспериментальных данных