2.2 Переменные процентные ставки

Переменная - изменяющаяся во времени процентная ставка.

Предположим, что в течение периода времени установлена ставка простых процентов , тогда приращение капитала за этот период составит .

Если в течение периода времени действует ставка простых процентов , то начисленные за этот период проценты составят .

Пусть число периодов начисления процентов - .

Тогда при установлении переменной, т.е. дискретно изменяющейся во времени процентной ставки, наращенная сумма определяется по формуле:

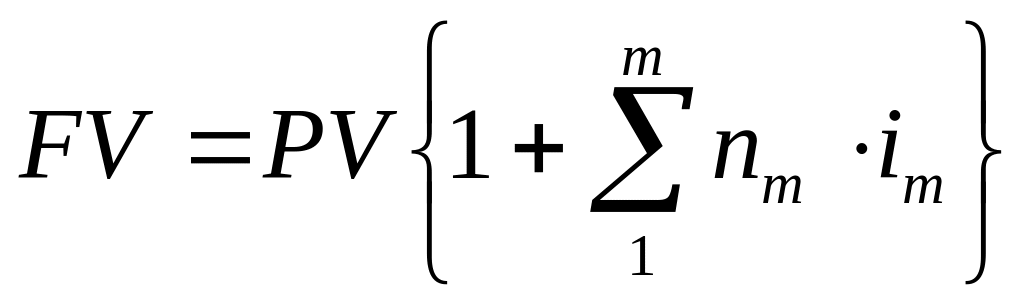, (2.3)

где — ставка простых процентов в периоде , где ;

2.3. Реинвестирование

Если по прошествии некоторого периода зафиксированная к данному моменту наращенная сумма инвестируется вновь, то такая операция называется реинвестированием (повторным инвестированием) или капитализацией полученных на каждом этапе наращения средств.

2.4. Математическое дисконтирование по простым процентам

В финансовой практике часто приходится решать задачу, обратную вычислению наращенной суммы, которая может быть сформулирована таким образом: определить сумму , которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период получить при установленной ставке процента требуемую наращенную сумму . Для решения этой задачи применяется операция дисконтирования.

Дисконтирование позволяет по известным наращенной сумме, процентной ставке и сроке финансовой операции определить современную стоимость этой наращенной суммы.

Другими словами дисконтирование позволяет определить, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму при условии, что на долг начисляются проценты по ставке .

В зависимости от вида процентной ставки применяются два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае при расчете применяют обычные (декурсивные), а во втором – авансовые проценты.

Выразив из формулы (2.1) , получим формулу математического дисконтирования:

, (2.5)

Здесь - современная стоимость наращенной (будущей) суммы денег ; - срок проведения финансовой операции (число процентных периодов); - процентная ставка.

Дисконтный множитель показывает, какую долю составляет первоначальная величина долга в его окончательной сумме .

В случае если срок финансовой операции задан в днях или в месяцах, из формулы (2.2) получим формулу математического дисконтирования для <1:

, (2.6)

где - длительность финансовой операции в днях (в месяцах); - число дней (месяцев в году).

2.5. Банковское дисконтирование (учет) по простым процентам

При начислении авансовых (антисипативных) процентов доход, получаемый кредитором, начисляется в начале периода финансовой операции относительно конечной суммы долга и выплачивается в момент предоставления кредита. Операция предварительного начисления процентов называется дисконтированием по учетной ставке, а также банковским или коммерческим учетом.

Банковский, или коммерческий учет используется при операциях с векселями и другими краткосрочными обязательствами.

Суть этой операции заключается в том, что банк или другие финансовые учреждения до наступления срока платежа по векселю покупает его у владельца (векселедержателя) и берет весь риск по получению денег на себя. При этом цена, по которой банк покупает вексель, должна быть меньше той суммы, которая должна быть выплачена по нему в конце срока (т.е. цены, выплачиваемой по векселю вместе с причитающейся ему частью дисконта).

Получив при поступлении срока деньги по векселю, банк, таким образом, реализует дисконт. Прежний владелец векселя с помощью учета векселя получает деньги ранее указанного в нем срока. То есть в определенном выигрыше оказываются обе стороны сделки.

При банковском учете проценты за пользованием ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.

Применительно к учету векселя, это означает, что проценты начисляются на сумму, которую должен выплатить должник в конце срока векселя. Ставка, по которой в этом случае начисляются проценты, отличается от декурсивной ставки процентов . Она называется учетной или дисконтной ставкой и обозначается .

формула банковского или коммерческого учета имеет вид:

(2.7)

Здесь – банковский дисконтный множитель.

В случае если срок финансовой операции задан в днях или в месяцах,

, (2.8)

где - срок вексельного кредита в днях (в месяцах); - число дней (месяцев в году). Обычно при вексельных расчетах принимают дней.

Очевидно, что операция учета векселя имеет смысл только в том случае, если , что равносильно неравенству .

Простая учетная ставка может быть использована при расчете суммы, которую получит владелец векселя при его погашении в момент наступления срока платежа. Для этого следует использовать формулу определения наращенной суммы:

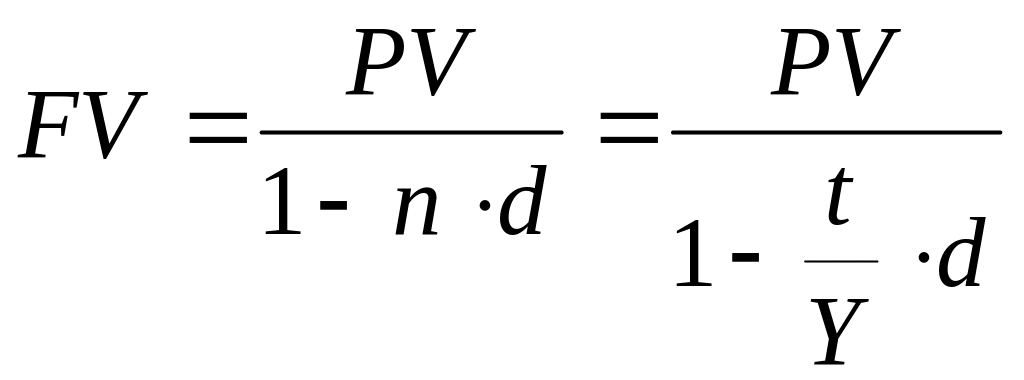(13)