Лекция 4

4.1. Потенциальные силы, потенциальная энергия и их взаимосвязь

Если в каждой точке простран­ства на помещенную туда частицу действует сила, то го­ворят, что частица находится в поле сил. Так, напри­мер, частица может находиться в поле сил тяжести, в по­ле упругих сил, в поле сил сопротивления (в потоке жид­кости, газа) и т. д.

Существуют силовые поля, в которых работа, совершае­мая над частицей силами поля, не зависит от пути меж­ду точками 1 и 2. Силы, обладающие таким свойством, называют консервативными или потенциальными. Очевидно, что для потенциальных сил выполняется равенство:

,

где A_1a2 - работа при перемещении точки из положения 1 в 2 по траектории 1- a- 2 в стационарном поле (рис. 4.), A_1b2 - вдоль траектории 1-b-2. Изменение направления движения точки вдоль траектории на проти­воположное вызывает изменение знака работы потенциальной силы, так как величина F_s в выражении (4.2) меняет свой знак, т.е. , Поэтому, , т.е. при перемещении материальной точки вдоль любой замкнутой траектории работа потенциальной силы тождественно равна нулю.

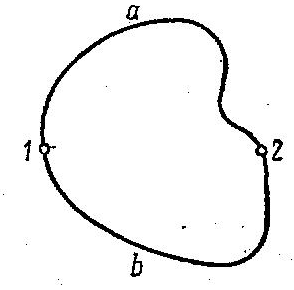
Рис.4.1

Примерами потенциальных сил могут служить силы всемир­ного тяготения, силы упругости, силы электростатического взаимодействия между заряженными телами.

Силы, не являющиеся потенциальными, называют непотенциальными. К числу непотенциальных сил относятся, например, силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положениями частицы и не рав­на нулю на любом замкнутом пути.

Потенциальная энергия частицы - это энергия, которая зависит только от ее положения относительно других частиц или тел, с которыми данная частица взаимодействует. Изменение положения частицы в поле сопровождается изменением ее потенциальной энергии, которое определяется совершаемой работой.

Изменение потенциальной энергии частицы, которая перемещается в поле потенциальных сил из точки 1 в точку 2, можно представить в виде:

,. (4.)

uде - работа перемещения частицы из точки 1 в точку 2, и - радиус-векторы точек 1 и 2 соответственно, и потенциальная энергия частицы соответственно в точках 1 и 2. Выражение (4.) можно представить через приращение потенциальной энергии ΔU:

A₁₂ = – ΔU , (4.2)

Из соотношения (4.2) видно, что работа потенциальных сил, действующих на частицу, равна убыли ее потенциальной энергии. При бесконечно малом перемещении частицы элементарная работа перемещения будет равна элементарному приращению потенциальной энергии частицы со знаком минус:

A = –dU. (4.3)

Можно показать, что сила поля равна градиенту по­тенциальной энергии частицы со знаком минус в данной точке поля Вектор силы в этом случае определяется соотношением:

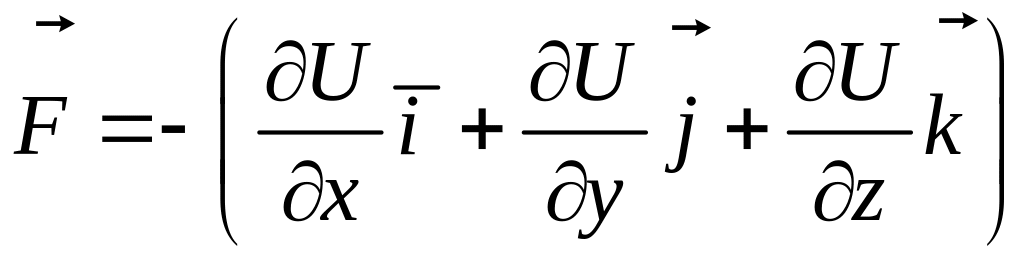. (4.4)

Выражение, стоящее в скобках называют градиентом потенциальной энергии U и обозначают grad U . Поэтому

. (4.5)

4.2. Непотенциальные силы

Силы, действующие на материальную точку, или тело, называются непотенциальными (диссипативными) если работа этих сил зависит от пути перемещения точки (тела).

Примером непотенциальных сил являются силы трения и сопротивления.

Природа сил трения может быть различной, но в результате их действия всегда происхо­дит превращение механической энергии во внутреннюю энергию тру­щихся тел, т. е. в энергию теплового движения их частиц. Рассмотрим виды трения, которые сопровождают движение тел.

Внутренним трением (вязкостью) называют явление, которое состоит в возникновении касательных сил, препятствующих перемещению частей одного и того же тела по отношению друг к другу (например, трение в жидкостях и газах).

Внешним трением называют явление, заключающееся в возникновении в месте контакта двух соприкасающихся твердых тел касательных сил, которые препятствуют относительному перемещению этих тел. Пример – трение скольжения или трение качения.

Экспериментально установлено, что сила трения скольжения F _ск подчиняется закону:

F _ск=μN, (4.6)

где μ - коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей, N - сила нормального давления.

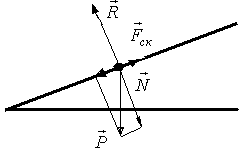
Рис.4.2

Причина возникновения трения качения состоит в том, что при качении по плоской поверхности кругового цилиндра или шара возникает деформация поверхности. Из-за деформации точка приложения силы реак­ции поверхности несколько смещается вперед, а линия действия этой силы отклоняется от вертикали назад (рис. 3-3). Нормальная составляю­щая реакции равна , а касательная составляющая является силой трения качения.

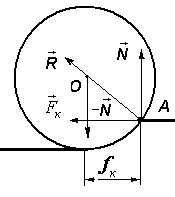
Рис.4.3

При равномерном качении сила трения качения компенсируется силой тяги, а сила реакции направлена вдоль прямой АО. Поэтому, момент этой силы относительно оси симметрии О катящегося тела равен нулю. Если r - радиус катящегося тела (цилиндра или шара), а f_к - величина смещения точки А приложения реакции , то из условия равенства нулю момента силы относи­тельно оси О следует формула:

, (4.7)

которая носит название закона Кулона для трения качения.