
Расчёт с учётом нелинейности
Т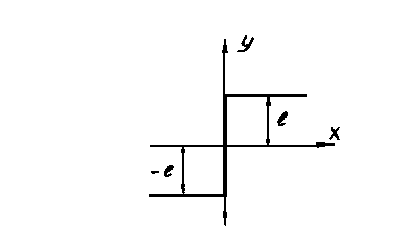 ип
нелинейности – Идеальная релейная.
ип
нелинейности – Идеальная релейная.
Параметры нелинейности:
l= 3.0
![]()
Построение фазового портрета.
![]()
![]()
Получаем уравнение 3 порядка: Рис. 24. Тип нелинейности.
![]()
Упрощаем его до 2 порядка. Для этого зануляем все коэффициенты, стоящие перед p в степени выше второй. Получаем следующее уравнение:
![]()
![]()
Тогда передаточная функция желаемой характеристики будет иметь вид:
![]()
Построение фазового портрета при помощи симулятора Matlab

Рис. 25. Схема системы в среде Matlab.
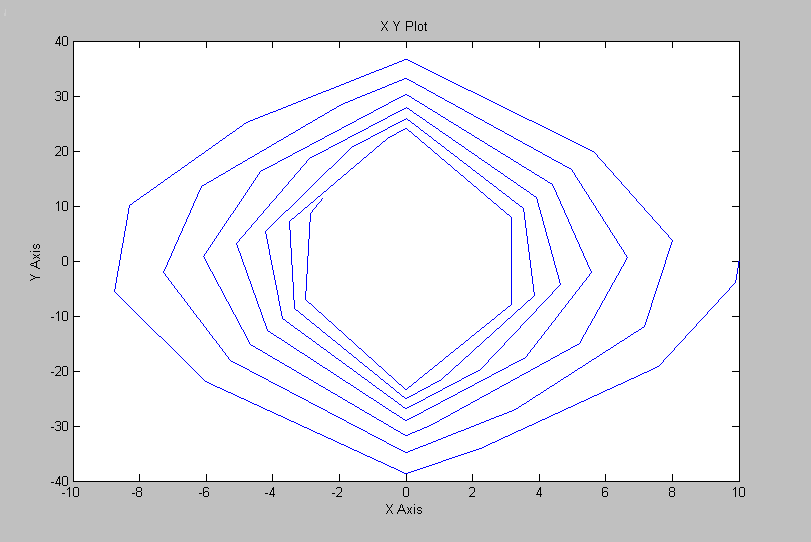
Рис. 26. Фазовый портрет.
Заключение.
Проведенные в работе расчеты являются неточными, так как существует множество факторов, которыми пренебрегали.
Во-первых, это несимметричность характеристики электронного усилителя и нелинейность характеристики генератора. Качественное влияние этого фактора выразиться в изменении коэффициента усиления системы при подаче равных по модулю, но разных по знаку величин.
Во-вторых, один из неучтенных факторов – это изменение нагрузки на валу двигателя. Так, например, при увеличении (уменьшении) нагрузки увеличиться (уменьшиться) статическая ошибка.
В-третьих, изменение номиналов сопротивлений при нагреве влияет на коэффициент усиления и может привести к увеличению установившейся ошибки.
Можно, сказать, что данная следящая система может выполнять поставленную задачу, то есть вращать объект управления при изменении входного воздействия не быстрее, чем 0.5 рад/с. Причем объектом управления может являться любое устройство весом не более 200 кг и линейными размерами не больше 1 м. При соблюдении этих условий данную систему после реализации можно использовать во многих сферах деятельности, например, в радиолокационных установках.
Список литературы.
1. Курс лекций по теории автоматического управления.
2. Солодовников В. В., Плотников В. Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования. Учебное пособие для вузов. – М.: Машиностроение, 1985. -536с., ил.
3. Бесекерский В. А., Попов Е. П. Теория САР. - М.: Наука , 1966г.
4. Брюханов и др. Теория автоматического управления. Учебное издание. Издательство «Высшая школа». 2000.
