Розділ 1 Тригонометричні рівняння. Їх види та способи розв’язування

1.1 Означення тригонометричних рівнянь

Свого часу велася запекла дискусія з приводу означення поняття тригонометричне рівняння. Тригонометричним пропонували називати:

• рівняння, в якому змінна входить лише під знак тригономет­ричної функції (в такому разі рівняння виду sin х+х=0 не на­лежить до тригонометричних; його пропонували називати трансцен­дентним);

• рівняння, в якому змінна входить під знак тригонометричної функції.

З цього приводу слід погодитись з думкою С. І. Новосьолова, який вважав, що розходження в означеннях тригонометричного рівняння не є принциповими. Важливо одне - немає загального методу розв'язування тригонометричних рівнянь. Слід наголосити на принциповій відмінності тригонометричних рівнянь від алгеб­раїчних: тригонометричні рівняння, в яких змінна входить лише під знак тригонометричної функції, або зовсім не мають розв'яз­ків, або мають їх безліч. Це пов'язано з властивістю періодичності тригонометричних функцій.

1.2 Види тригонометричних рівнянь та способи їх розв’язування Найпростіші тригонометричні рівняння

Як правило, розв’язування тригонометричного рівняння зводиться до розв’язування рівнянь виду sin t = a, cos t = a, tg t = a, ctg t = a, які називають найпростішими. Способи розв’язування таких рівнянь детально вивчаються в курсі алгебри та початків аналізу 10-го класу.

Зупинимось на більш складних видах тригонометричних рівнянь.

Розв’язування тригонометричних рівнянь способом розкладанням на множники

Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один зі співмножників дорівнює нулю, а інші при цьому не втрачають змісту. Розглянемо цей спосіб.

Приклад. Розв’яжіть рівняння .

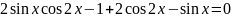Розв’язання. Згрупуємо доданки у лівій частині рівняння:

.

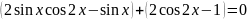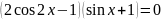
Враховуючи умову рівності нулю, маємо:

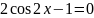або .

Кожне з цих рівнянь легко звести до найпростішого:

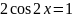
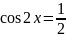
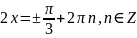
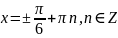
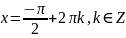
Відповідь: ;

.

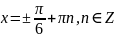Розв’язування тригонометричних рівнянь, що зводяться до квадратних

У курсі алгебри 8-го класу було вивчено способи розв’язування квадратних рівнянь, які використовуються і при розв’язуванні окремих випадків тригонометричних рівнянь.

Приклад. Розв’яжіть рівняння .

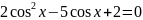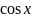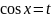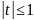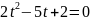Розв’язання. Дане рівняння є квадратним відносно . Нехай , де , тоді одержимо рівняння . Розв’язавши його, знайдемо ; 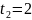. Значення не задовольняє умову , отже:

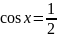
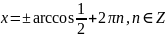
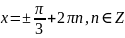
Відповідь:

Розв’язування однорідних рівнянь

Рівняння виду 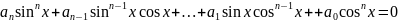називається однорідним рівнянням n-го степеня відносно синуса і косинуса. Це такі рівняння, у яких ліва частина є многочленом, у кожному члені якого сума показників степенів синуса і косинуса одного і того самого аргументу однакова, а права – 0. однорідні рівняння n-го степеня відносно синуса і косинуса розв’язують діленням обох частин на . Проте попередньо слід довести, що .

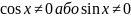Однорідне тригонометричне рівняння 1-го степеня -

це рівняння виду: 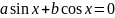, де a і b

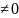
Приклад. Розв’яжіть рівняння .

Розв’язання. Поділимо обидві частини рівняння на . Оскільки корені рівняння 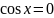не є коренями вихідного рівняння, т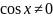о . Маємо:

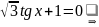
Відповідь: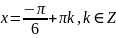

Однорідне тригонометричне рівняння 2-го степеня -

це рівняння виду: 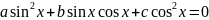, де a, b і c

Приклад. Розв’яжіть рівняння .

Розв’язання.

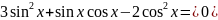
, тому що .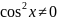

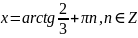
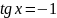
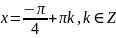
Відповідь: ;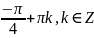

Однорідні тригонометричні рівняння n-го степеня

розв’язуються аналогічно до вищеназваних.