Кременчуцька загальноосвітня школа І – ІІІ ступенів навчання №16

11 Клас

Ванжула Олена Геннадіївна

Реферат на тему: «Тригонометричні рівняння. Їх види та способи розв’язування»

Вчитель

Ванжула Лілія Станіславівна

Кременчук - 2011

ЗМІСТ

ВСТУП...........................................................................................................3

Розділ 1. Тригонометричні рівняння. Їх види та способи розв’язування….…………………………………………...4

1.1 Означення тригонометричних рівнянь………………4

1.2 Види тригонометричних рівнянь та способи їх розв’язування…………………………………………4

• Найпростіші тригонометричні рівняння…………4

• Розв’язування тригонометричних рівнянь способом розкладання на множники……………..4

• Розв’язування тригонометричних рівнянь, що зводяться до квадратних…………………………..5

• Розв’язування однорідних рівнянь……………….5

• Однорідне тригонометричне рівняння 1-го степеня……………………………………..…….6

• Однорідне тригонометричне рівняння 2-го степеня…………………………...………………6

• Однорідне тригонометричне рівняння n-го степеня…………………………………………...6

• Розв’язування тригонометричних рівнянь виду 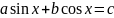………………………………..6

• Рівняння, що розв’язуються за допомогою заміни 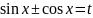……………………………………7

• Розв’язування тригонометричних дробово-раціональних рівнянь…………………………..….8

• Графічний спосіб розв’язування тригонометричних рівнянь………………………..9

• Тригонометричні рівняння, що містять ірраціональність……………………………………9

• Тригонометричні рівняння з параметром……….10

Висновок………………………………….………………………………11

Список використаної літератури……………………….……………..12

ВСТУП

°	sin	cos	tg	ctg
1	0,02	1,00	0,02	57,29	89
2	0,03	1,00	0,03	28,64	88
3	0,05	1,00	0,05	19,08	87
4	0,07	1,00	0,07	14,30	86
5	0,09	1,00	0,09	11,43	85
6	0,10	0,99	0,11	9,51	84
7	0,12	0,99	0,12	8,14	83
8	0,14	0,99	0,14	7,12	82
9	0,16	0,99	0,16	6,31	81
10	0,17	0,99	0,18	5,67	80
11	0,19	0,98	0,19	5,14	79
12	0,21	0,98	0,21	4,70	78
13	0,22	0,97	0,23	4,33	77
14	0,24	0,97	0,25	4,01	76
15	0,26	0,97	0,27	3,73	75
16	0,28	0,96	0,29	3,49	74
17	0,29	0,96	0,31	3,27	73
18	0,31	0,95	0,32	3,08	72
19	0,33	0,95	0,34	2,9	71
20	0,34	0,94	0,36	2,75	70
21	0,36	0,93	0,38	2,61	69
22	0,37	0,93	0,40	2,48	68
23	0,39	0,92	0,42	2,36	67
24	0,41	0,91	0,45	2,25	66
25	0,42	0,91	0,47	2,14	65
26	0,44	0,90	0,49	2,05	64
27	0,45	0,89	0,51	1,96	63
28	0,47	0,88	0,53	1,88	62
29	0,48	0,87	0,55	1,80	61
30	0,50	0,87	0,58	1,73	60
31	0,52	0,86	0,60	1,66	59
32	0,53	0,85	0,62	1,60	58
33	0,54	0,84	0,65	1,54	57
34	0,56	0,83	0,67	1,48	56
35	0,57	0,82	0,70	1,43	55
36	0,59	0,81	0,73	1,38	54
37	0,60	0,80	0,75	1,33	53
38	0,62	0,79	0,78	1,28	52
39	0,63	0,78	0,81	1,23	51
40	0,64	0,77	0,84	1,19	50
41	0,66	0,75	0,87	1,15	49
42	0,67	0,74	0,90	1,11	48
43	0,68	0,73	0,93	1,07	47
44	0,69	0,72	0,97	1,04	46
45	0,71	0,71	1,00	1,00	45
	cos	sin	сtg	tg	°

Тригонометрія - слово грецьке і в буквальному перекладі означає вимірювання трикутників ( - трикутник,  - вимірюю). В даному випадку вимірювання трикутників слід розуміти як розв’язування трикутників, тобто визначення сторін, кутів та інших елементів трикутника, якщо дано лише деякі з них. Велика кількість практичних завдань, а також завдань планіметрії, стереометрії, астрономії та інших наводяться до задач розв’язування трикутників. Вперше способи розв’язування трикутників, засновані на відношеннях між сторонами і кутами трикутника, були знайдені давньогрецькими астрономами Гиппархом (2 ст. До н. Е..) і Клавдієм Птолемеєм (2 ст. Н. Е..). Пізніше такі відношення почали називати тригонометричними функціями.

Значний внесок у розвиток тригонометрії внесли арабські вчені аль-Батанов (850-929) і Абуль-Вефа Мухамед-бен Мухамед (940-998), який склав таблиці синусів і тангенсів через 10' з точністю до 1/604. Теорему синусів уже знали індійський вчений Бхаскара та азербайджанський астроном і математик Насіреддін Тусі Мухамед. Теорему тангенсів довів Йоганн Мюллер (1436-1476). Довгий час тригонометрія носила чисто геометричний характер. Такою вона була ще і в середньовіччі. Поступово тригонометрія органічно увійшла в математичний аналіз, механіку, фізику і технічні дисципліни. Починаючи з XVII ст., тригонометричні функції почали застосовувати до розв’язування рівнянь, задач механіки, оптики, електрики, радіотехніки, розповсюдження хвиль, для вивчення змінного електричного струму тощо. Тому тригонометричні функції всебічно і глибоко досліджувалися . Знання графіків та властивостей тригонометричних функцій дозволяють знаходити розв’язки тригонометричних рівнянь.