Таким образом, суммарный иск к страховой компании

уменьшается и становится равным

.

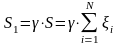Однако одновременно уменьшается и капитал передающей компании.

До заключения договора перестрахования капитал передающей компании был равен

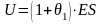, (1)

где 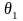- относительная страховая надбавка, обеспечивающая страхователю определенную вероятность неразорения . Заключение договора перестрахования приводит к выплате перестраховочной компании суммы

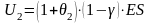, (2)

где 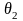- относительная страховая надбавка, установленная перестрахователем. Поэтому капитал передающей компании станет равным:

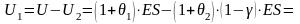
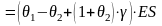. (3)

Следовательно, вероятность неразорения передающей компании становится равной

,

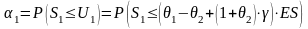или

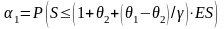. (4)

При аппроксимации нормальным распределением, получаем:

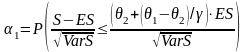, (4´)

где

-

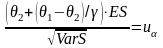квантиль нормального распределения.

Отсюда следует, что для максимизации вероятности неразорения необходимо выбрать параметр таким образом, чтобы максимизировать величину .

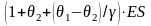Видно, что:

а) Если 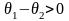, то есть 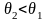, то максимум достигается при 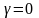. Другими словами, если перестраховочная компания устанавливает меньшую страховую надбавку , то нужно перестраховать все иски. При этом вероятность разорения будет равна нулю. Однако этот случай практического интереса не имеет, так как реально справедливо равенство .

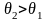б) Если 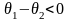, то есть , то 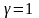. Другими словами, если перестраховочная компания устанавливает большую страховую надбавку, то от перестрахования нужно вообще отказаться.

в) Если 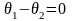, то есть 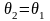, то вероятность неразорения от не зависит. Другими словами, может принимать все значения в промежутке .

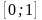Следовательно, в рамках простейшей модели риска (без учета неоднородности договоров, резервов и различного рода издержек) чистое пропорциональное перестрахование не представляет никакого интереса с точки зрения математики.

Пропорциональное эксцедентное перестрахование

При этом виде перестрахования предел удержания может меняться по рискам в пределах 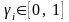, , 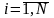где - количество различных договоров страхования. Тогда перестраховочной компании будет выплачена сумма:

.

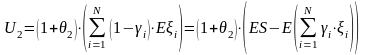Поэтому капитал передающей компании становится равным

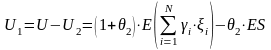, (5)

а вероятность неразорения можно вычислить как

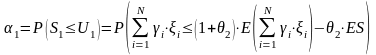. (6)

Рекомендуется устанавливать значения 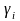таким образом, чтобы 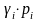оставалось постоянным. То есть по некоторым рискам удержание будет полным, а по остальным 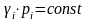. Здесь 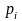- полная страховая премия по - ому договору. В соответствующих договорах оформляют таблицу уровней удержания, величина которых уменьшается с увеличением интенсивности рисков.

38. Сущность договоров перестрахования Перестрахование превышения потерь.

устанавливается некоторый предел удержания руб. Если величина индивидуального иска не превосходит (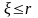 ), то передающая компания оплачивает иск самостоятельно, а если 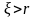, то компания выплачивает сумму руб., а оставшуюся часть 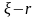оплачивает перестраховочная компания.

Таким образом, иск разбивается на две части: иск 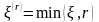к передающей компании, и иск 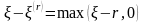к перестраховочной компании.

Пусть было перестраховано однотипных договоров с исками 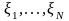, которые являются независимыми и одинаково распределенными случайными величинами. Тогда суммарный иск к передающей компании, равный 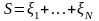уменьшается до величины 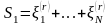. Однако, уменьшается и капитал передающей компании. Если до заключения договора перестрахования он был равен:

,

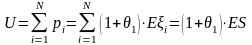то заключение договора перестрахования приводит к необходимости выплаты перестраховочной компании суммы

.

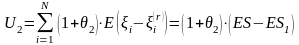Поэтому капитал передающей компании становится равным

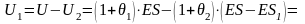
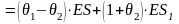, (7)

а вероятность неразорения будет вычисляться по формуле:

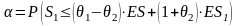. (8)

Если применить приближение нормальным распределением, то можно записать

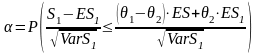. (8´)