Тогда плата за страховку будет иметь вид:

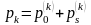, (33)

где 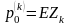- нетто-премия по - ому договору, а 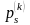- соответствующая страховая надбавка, которая вычисляется аналогично краткосрочному страхованию жизни.

В простейшем случае, когда страховая надбавка делится пропорционально математическим ожиданиям, получаем:

. (34)

При более сложных моделях долгосрочного страхования не всегда удается выразить:

а) вероятность неразорения в виде простой формулы вида (32);

б) нетто-премии и страховые надбавки в виде (34).

Однако в любом случае для расчета страховых премий необходимо уметь вычислять современную стоимость страховых выплат, их математические ожидания и дисперсии.

Дисперсии, в некоторых случаях, вычисляются достаточно просто. Предположим, что функция принимает только два значения 0 и 1. Тогда

,

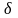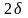другими словами, дисперсия при силе роста равна разности между современной стоимостью при силе роста и квадратом при исходной силе роста .

23. Полная пожизненная рента.

Во многих случаях более предпочтительным для застрахованного является не получение единовременной выплаты, а регулярный доход в течение определенного периода или пожизненно. Такие регулярные выплаты через равные промежутки называют страховой рентой или аннуитетом.

Полная пожизненная рента

Простейшая пожизненная рента пренумерандо описывается следующим образом: начиная с момента времени 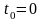, человек один раз в начале каждого года начинает получать определенную постоянную сумму, которую примем в качестве единицы измерения денежных сумм. Выплаты этой суммы производятся только во время жизни человека.

Обозначим через х возраст человека в момент времени начала платежей. Тогда выплаты будут производиться в моменты времени 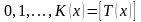, где - остаточная продолжительность жизни. То есть имеем дело с годовой рентой пренумерандо со случайным числом выплат 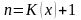. Найдем современную стоимость такой ренты

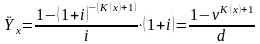, (1)

которая является случайной величиной. Здесь - годовая ставка дисконтирования.

Так как 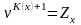- современная стоимость полного дискретного страхования жизни, то

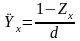, (2)

поэтому расчет характеристик пожизненной ренты можно свести к расчету характеристик соответствующего дискретного страхования жизни.

Найдем актуарную современную стоимость пожизненной ренты (нетто-премию):

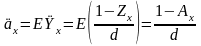, (3)

или

. (4)

Для расчета защитной надбавки и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию , а именно

, (5)

где 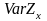вычисляется так же, как и в предыдущей главе.

Формула (4) получен методом суммарной выплаты, когда пожизненная рента рассматривается как сумма случайного числа 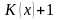детерминированных слагаемых. Можно применить и другой метод – метод текущего платежа, который рассматривает эту ренту как сумму детерминированного числа случайных слагаемых.

если при страховании рент речь пойдет о ренте постнумерандо, когда страховые выплаты будут производиться в конце соответствующего периода, то вычисление современной стоимости будет производиться по формуле:

.

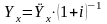24. Временная пожизненная рента.

Временная п - летняя пожизненная рента выплачивается начиная с момента времени пожизненно, но не более, чем п лет, поэтому современная стоимость такой ренты будет равна

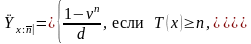(6)

Учитывая, что современная стоимость п – летнего дискретного смешанного страхования жизни определяется как:

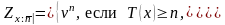
получаем:

.

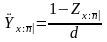Поэтому современная актуарная стоимость такой ренты будет вычисляться как

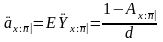(7)

где 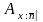- нетто-премия при дискретном смешанном страховании жизни.

Для расчета защитной надбавки и оценки вероятности разорения компании необходимо уметь вычислять и дисперсию 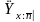, а именно

.

Можем 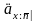выразить и через характеристики жизни, рассмотренные ранее:

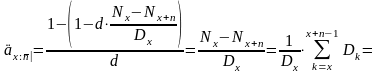
, (8)

25. Отсроченная пожизненная рента.

Отсроченная на m лет пожизненная рента представляет собой серию выплат единичной суммы, начиная с момента времени 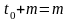, до тех пор, пока человек жив. Тогда современная стоимость такой ренты равна

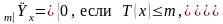(9)

Так как

,

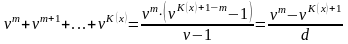то

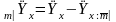. (10)

Поэтому актуарная стоимость этой ренты будет равна

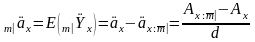, (11)

или

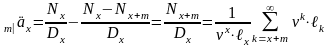. (12)

26. Актуарная современная стоимость и актуарная наращенная сумма.

некий пенсионный фонд, в который человек в момент времени вносят по единичной сумме. К моменту времени эта сумма возрастет до . Однако, если в момент времени все человек имеют возраст x лет, то к моменту времени в живых останется в среднем 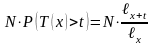человек. Поэтому на каждого оставшегося в живых участника фонда будет приходиться сумма

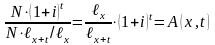. (13)

Величину 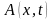называют актуарным наращением или актуарным накоплением. Она больше обычного множителя наращения 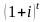, так как происходит уменьшение числа живых участников фонда, претендующих на соответствующую им долю средств данного фонда.

Следовательно, для получения единичной суммы в момент времени , каждый из застрахованных должен внести в момент времени сумму

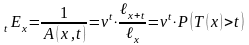. (14)

Величина 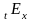называется актуарным коэффициентом дисконтирования для человека в возрасте х на отрезке 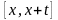. Этот коэффициент, при равной величине выплат, всегда меньше современной стоимости обычной финансовой ренты, так как взносы по страховой ренте собираются со всех, а выплаты производятся только дожившим до сроков ее выплаты.

Коэффициенты и можно выразить и через упрощающую функцию :

,

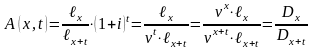и

.

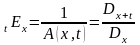Тогда и введенные выше актуарные стоимости рент можно записать как

,

,

.

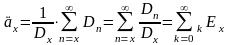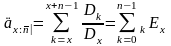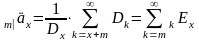Здесь можно отметить, например, что 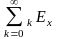представляет собой среднюю сумму, которую надо внести, чтобы получить единичную сумму в каждый из моментов .

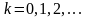27. Пожизненные постоянные p - срочные ренты.

Ежегодные ренты,встречаются значительно реже, чем ренты, выплачиваемые несколько раз в год (полугодовые, ежеквартальные, ежемесячные).

Полная пожизненная рента

Полная пожизненная р – срочная рента пренумерандо описывается следующим образом: начиная с момента времени человек в возрасте лет будет получать раз в год по 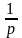у.е. в начале каждой из 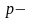х долей года, то есть в моменты времени

.

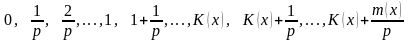Здесь 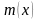- целое число из промежутка 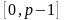такое, что

.

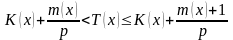Тогда приведенная стоимость такой ренты в момент времени будет вычисляться как

, (15)

а актуарная стоимость будет равна

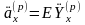. (16)

Временная пожизненная рента

В этом случае период выплат будет ограничен некоторым сроком в n лет. То есть, если человек проживет еще n лет 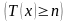, то будет произведено 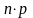выплат; а если же человек умрет до достижения возраста n лет 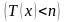, то будет произведено 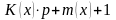выплат величиной у.е. каждая.

В предположении о равномерном распределении времени жизни для дробных возрастов можем получить следующую формулу для вычисления актуарной стоимости такой ренты

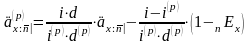. (17)

Здесь 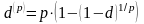- номинальная ставка дисконтирования, обращаемая с частотой , 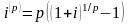- номинальная процентная ставка.

Если в равенстве (17) перейти к пределу при , получим аналогичную формулу и для полной пожизненной ренты:

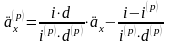. (18)

х - целое число лет.

28. Непрерывные пожизненные ренты.

Пусть в полной пожизненной ренте, выплачиваемой с частотой , . За малый промежуток времени поступит сумма . Тогда приведенную стоимость полной непрерывной пожизненной ренты в момент времени можем вычислить как

.

С учетом того, что , можем написать:

.

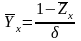Тогда актуарная приведенная стоимость такой ренты будет равна

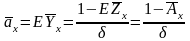. (19)

Можем 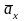выразить и через упрощающие функции

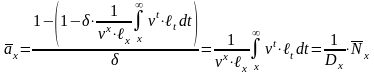. (20)

В случае временной непрерывной пожизненной ренты платежи производятся не более, чем лет, то есть период платежей равен 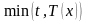. Тогда приведенная стоимость такой ренты будет равна

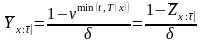, (21)

а актуарная стоимость:

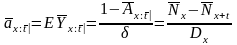. (22)

29. Схема расчета периодических нетто-премий. Периодические нетто-премии при

полном дискретном страховании жизни.

СХЕМА РАСЧЕТА НЕТТО-ПРЕМИЙ

Предположим, что страховая премия выплачивается в виде серии платежей в течение некоторого срока с момента заключения договора страхования. При такой периодической уплате взносов застрахованный выполняет свои обязательства в рассрочку. Однако стоимость обязательств компании не зависит от способа уплаты страховых премий.

При расчете величины периодически уплачиваемых премий необходимо учитывать как процентный доход от инвестиций, так и демографические факторы (смертность). Последний фактор оказывает существенное влияние на величину взносов, так как не все застрахованные успевают уплатить все предусмотренные контрактом взносы.

В общем виде, схема расчета нетто-премий может быть представлена следующим образом. Пусть - искомая нетто-премия. Тогда современная актуарная стоимость обязательств застрахованного 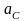будет функцией , то есть 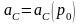. Актуарная современная стоимость финансовых обязательств компании 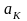также является функцией : 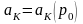. И для вычисления необходимо применить принцип финансовой эквивалентности обязательств страховой компании и застрахованного, а это означает, что необходимо решить уравнение:

, (1)

которое представляет собой условие равенства обязательств застрахованного и страховой компании на момент заключения договора страхования.

Отметим, что, как и ранее, полная периодическая премия состоит из нескольких частей: периодическая нетто-премия , защитная (страховая) надбавка 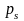и расходы, возмещающие организационные затраты.

Применим теперь общую схему (1) к различным вариантам страхования.

Полное дискретное страхование жизни

Пусть плата за страховку вносится в начале каждого года с момента заключения договора страхования в сумме 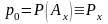в течение всей жизни. Так как договор страхования вступает в силу только после получения компанией первого взноса, рента страховых платежей (премий) является всегда рентой пренумерандо. Тогда актуарная приведенная стоимость потока премий на момент заключения договора будет равна:

.

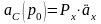Страховая компания выплачивает единичную сумму в конце года смерти 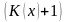застрахованного. Актуарная современная стоимость этой суммы на момент заключения договора страхования будет равна , то есть 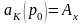. Следовательно, из равенства (1) получаем:

,

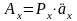или

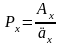. (2)

Формула (2) показывает во сколько раз величина ежегодного взноса 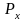меньше величины единовременно уплачиваемого взноса . Поэтому величину коэффициента приведения 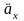называют еще коэффициентом рассрочки.

Если период уплаты нетто-премий ограничен, например. n годами, то обязательства застрахованного будут выглядеть как

,

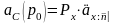и ежегодная нетто-премия будет равна:

. (3)

30. Периодические нетто-премии при непрерывном страховании жизни.

Полное непрерывное страхование жизни

Пусть теперь единичное страховое возмещение выплачивается в момент смерти 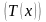застрахованного. Актуарная стоимость этой суммы в момент заключения договора страхования равна:

.

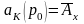Обязательства застрахованного заключаются в ежегодной выплате суммы 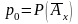, актуарная стоимость, которой на момент заключения договора страхования будет равна:

.

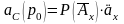Тогда, из условия (1) финансовой эквивалентности обязательств застрахованного и страховой компании, получаем:

,

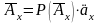или

. (4)

Учитывая, что

,

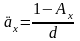можем последнюю формулу представить как:

; (4´)

а если принять предположение о равномерном распределении жизни для дробных возрастов, то

.

Если период уплаты нетто-премий ограничен, например. n годами, то обязательства застрахованного будут выглядеть как

,

и ежегодная нетто-премия будет равна:

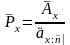. (5)

Полное непрерывное страхование жизни с выплатой премий т раз в год

В этом случае годовая нетто-премия выплачивается m раз в год по 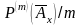единиц. Тогда актуарная стоимость обязательств застрахованного на момент заключения договора будет равна

.

Обязательства страховой компании остались такими же, как в § 2.2. Поэтому

,

то есть

. (6)

Учитывая формулу (4), можно выразить эту нетто-премию через ежегодную нетто-премию :

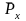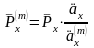. (7)

37. Сущность договоров перестрахования Пропорциональное перестрахование

Перестрахование играет существенную роль в обеспечении финансовой устойчивости страховых компаний. На развивающихся же страховых рынках оно стало одним из важнейших инструментов повышения финансовой устойчивости компаний.

СУЩНОСТЬ ДОГОВОРОВ ПЕРЕСТРАХОВАНИЯ

Клиент заключает договор страхования со страховой компанией для того, чтобы избавиться от финансовых потерь, связанных с неопределенностью распределения тех или иных случайных событий. После заключения договора страхования клиент избавился от этого риска за фиксированную (неслучайную) плату (без учета издержек):

.

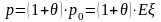Другими словами, клиент идет на небольшие расходы с тем, чтобы избавиться от случайных потерь, которые хоть и маловероятны, но могут быть катастрофически большими для него.

Однако сам риск не исчез – его приняла на себя страховая компания, которая обеспечивает себе малую вероятность разорения, имея большой портфель договоров страхования. Тем не менее, возможны очень большие иски, которые могут привести к разорению компании, то есть существует опасность финансовых потерь, связанных с неопределенностью появления очень больших исков. Поэтому страховая компания попадает в ситуацию, аналогичную той, в которой находились ее клиенты до заключения договора страхования.

Для решения этой проблемы страховая компания может поступить так же, как и ее клиенты – застраховать свой риск в другой страховой компании. Такой вид страхования называется перестрахованием.

Компания, заключившая договоры непосредственно с клиентом и желающая перестраховать часть своего риска, называется передающей компанией («цедентом»), а компания, которая ее страхует, называется перестраховочной компанией («цессионаром»).

Существуют различные причины, по которым страховые компании вынуждены обращаться к перестрахованию. Например, это недавно созданные компании, финансовое положение которых пока еще неустойчиво из-за недостаточного размера его страхового портфеля, или даже более крупная страховая компания при покрытии страховых рисков «лиц, занимающих ключевые посты» («jumbo risques»), или при обеспечении наследственного права в крупных размерах.

При перестраховании могут перестраховываться как чрезмерно большие частные иски, так и суммарный иск за определенный период. Основное деление договоров перестрахования на различные типы связано с видом разделения ответственности между передающей компанией и перестраховочной компанией. Существуют многочисленные формы перестрахования, которые в техническом плане можно разделить на две категории: договоры пропорционального перестрахования и договоры перестрахования превышения потерь.

Пропорциональным перестрахованием называется такой вид перестрахования, при котором передающая компания самостоятельно оплачивает некоторую долю 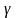от каждого иска 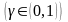, а перестраховочная компания удовлетворяет оставшуюся долю иска 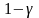. Параметр называется пределом удержания.

Перестрахованием превышения потерь называется такой вид перестрахования, при котором передающая компания самостоятельно оплачивает все иски до некоторого предела 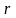руб., а если иск превышает руб., то на остаток суммы предъявляет иск к перестраховочной компании. Параметр также называется пределом удержания. Если это правило применяется к общему иску за некоторый период, то такое перестрахование называется перестрахованием, останавливающим потери, или перестрахованием на базе эксцедента убыточности. Параметр в этом случае называется франшизой или вычитаемой франшизой.

Для перестраховочной компании эта операция выглядит как обычное страхование, поэтому плата за перестрахование риска будет равна 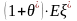, где 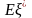– ожидаемый иск к перестраховочной компании, 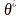– относительная страховая надбавка, установленная перестраховочной компанией. Будем рассматривать договоры перестрахования только с точки зрения предающей компании, поэтому считаем фиксированной величиной. И основная проблема будет заключаться в выборе предела удержания, оптимального с точки зрения передающей компании. Следует отметить, что перестраховочные тарифы также должны базироваться на таблицах отбора риска

ПРОПОРЦИОНАЛЬНОЕ ПЕРЕСТРАХОВАНИЕ

Чистое пропорциональное перестрахование

При этом виде перестрахования страховщик передает перестраховщику одинаковую долю от всех рисков страхового портфеля, которые он принимает в одной и той же отрасли. То есть перестраховщик покрывает одну и ту же часть исков во всех страховых случаях, оплаченных страховщиком.

Пусть портфель страховой компании состоит из договоров страхования с исками 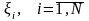. Тогда, при наступлении страхового случая, сумму 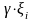платит передающая компания, а сумму 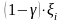выплачивает перестраховочная компания.