
- •Таким образом, плотность распределения вероятностей
- •Если справедливо предположение о равномерном распределении смертей внутри года, то апроксимируется линейной функцией вида:
- •Из курса теории вероятностей известно, что в случае дискретных случайных величин вида:
- •Для упрощения записи вводят и выражения:
- •Нетто-премия будет вычисляться как:
- •При этом виде страхования нетто-премия вычисляется по формуле
- •Нетто-премия вычисляется как
- •Тогда плата за страховку будет иметь вид:
- •Таким образом, суммарный иск к страховой компании
- •И вероятность неразорения будет наибольшей, если функция
Из курса теории вероятностей известно, что в случае дискретных случайных величин вида:
-
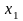
…
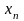
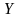

…
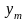
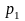
…
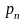
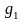
…
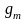
закон
распределения суммы
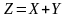 можно найти по следующему правилу:
можно найти по следующему правилу:
а)
возможные значения
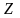 представляют собой суммы
представляют собой суммы
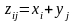 ;
;
б)
вероятность возможного значения
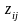 равна произведению вероятностей
слагаемых:
равна произведению вероятностей
слагаемых:
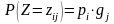 ,
,
то
есть вероятность вида
 будет вычисляться как
будет вычисляться как
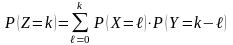 .
.
Вычисление этих вероятностей удобно представить в виде следующей матрицы вероятностей:
-

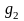
…
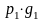
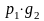
…
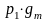
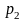
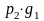
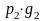
…

…
…
…
…
…
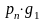
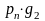
…
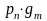
Если рассматривается
сумма нескольких независимых случайных
величин вида
,
то суммирование следует проводить
последовательно, вычисляя суммы
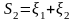 ,
,
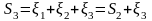 ,
…,
,
…,
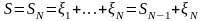 .
.
14.Приближенные методы расчета вероятности разорения
При
больших
применяют приближенные методы, основанные
на том, что закон распределения
вероятностей суммы
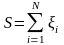 можно достаточно точно аппроксимировать,
например, законом распределения Пуассона
или нормальным законом распределения
вероятностей.
можно достаточно точно аппроксимировать,
например, законом распределения Пуассона
или нормальным законом распределения
вероятностей.
Применение
нормального закона основано на центральной
предельной теореме, которая утверждает,
что при некоторых, весьма общих
предположениях, закон распределения
суммы большого числа независимых
случайных величин
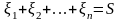 стремится к асимптотически нормальному
распределению с параметрами
стремится к асимптотически нормальному
распределению с параметрами
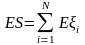 ,
,
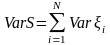 .
.
Известно,
что если
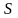 имеет асимптотически нормальное
распределение, то справедливо равенство
имеет асимптотически нормальное
распределение, то справедливо равенство
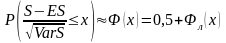 ,
(8)
,
(8)
где
функция распределения вероятностей
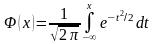 и функция Лапласа
и функция Лапласа
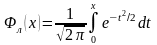 протабулированы в соответствующих
таблицах.
протабулированы в соответствующих
таблицах.
Полезно
иметь также таблицу значений квантилей
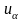 ,
отвечающих достаточно малой вероятности
разорения
,
отвечающих достаточно малой вероятности
разорения
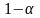 ,
то есть таблицу вероятностей вида
,
то есть таблицу вероятностей вида
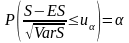 :
:
1-α |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
|
2,33 |
2,05 |
1,88 |
1,75 |
1,645 |
которая
соответствует определенным значениям
из таблицы значений функции
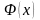 .
.
вероятность неразорения компании задается формулой:
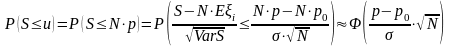 .
.
И
если мы хотим, чтобы вероятность
неразорения была равна
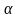 ,
то величина
,
то величина
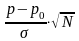 должна равняться квантилю
,
то есть
должна равняться квантилю
,
то есть
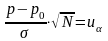 ,
,
или
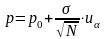 ,
(9)
,
(9)
где
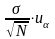 - страховая надбавка, а относительная
страховая надбавка будет равна:
- страховая надбавка, а относительная
страховая надбавка будет равна:
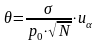 .
(10)
.
(10)
Чем
меньше
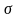 (рассеивание возможных значений страховых
выплат относительно среднего значения
),
или чем больше количество застрахованных
,
тем меньше относительная надбавка
(рассеивание возможных значений страховых
выплат относительно среднего значения
),
или чем больше количество застрахованных
,
тем меньше относительная надбавка
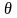 .
.
15. Принципы назначения страховых премий.
Вычисление платы за страховку
Пусть в компании
застраховано
человек. Возьмем в качестве платы по
-
ому договору величину
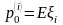 .
Тогда резервный фонд (капитал) компании
равен
.
Тогда резервный фонд (капитал) компании
равен
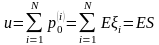 ,
,
и вероятность разорения определяется как
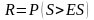 .
.
В случае нормального распределения получаем
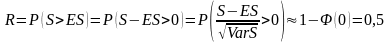 .
.
в плату за
страховку включаtv некоторую
надбавку
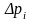 ,
которая бы компенсировала элементы
случайности
.
,
которая бы компенсировала элементы
случайности
.
То есть плата за страховку будет теперь иметь вид:
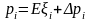 .
(11)
.
(11)
Тогда капитал компании будет равен
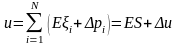 ,
,
где
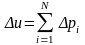 .
.
Найдем вероятность неразорения компании
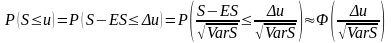 .
.
И если мы хотим,
чтобы вероятность неразорения компании
была равна
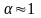 ,
то
,
то
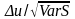 должен быть равен квантилю
,
то есть
должен быть равен квантилю
,
то есть
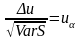 ,
,
или
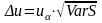 - (12)
- (12)
величина добавочной
суммы
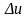 .
.
Так как в
выражение (12) входит среднее квадратическое
отклонение
 ,
то добавочная сумма
действительно учитывает риск, связанный
с непредсказуемостью убытков.
,
то добавочная сумма
действительно учитывает риск, связанный
с непредсказуемостью убытков.
Распределение пропорционально ожидаемому убытку
Разделим сумму
пропорционально ожидаемому убытку
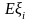 ,
то есть
,
то есть
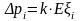 .
(13)
.
(13)
Просуммируем (13) по
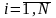 :
:
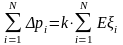 ,
,
или
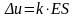
и
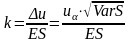 .
.
Тогда
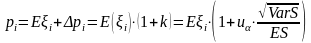 .
(14)
.
(14)
Здесь
- нетто-премия,
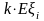 - страховая надбавка,
- страховая надбавка,
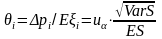 - (14’)
- (14’)
относительная страховая надбавка.
Распределение пропорционально дисперсиям
Недостатком
назначения индивидуальных премий по
правилу (13) является то, что оно
несправедливо по отношению к договорам,
которые имеют малую дисперсию
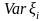 ,
и потому оплачивают в большей степени
случайности, связанные с договорами с
большей дисперсией.
,
и потому оплачивают в большей степени
случайности, связанные с договорами с
большей дисперсией.
Поэтому можно разделить сумму пропорционально дисперсиям:
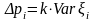 .
(15)
.
(15)
Просуммировав по , получаем
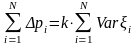 ,
,
или
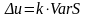 .
.
Отсюда
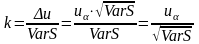 .
.
Следовательно,
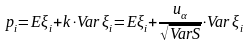 (16)
(16)
и относительная страховая надбавка
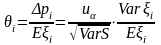 .
(16’)
.
(16’)
Распределение пропорционально средним квадратическим отклонениям
Если же разделить сумму пропорционально средним квадратическим отклонениям:
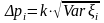 ,
(17)
,
(17)
то, просуммировав по , получаем:
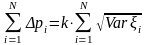 ,
,
или
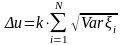 .
.
Отсюда следует, что
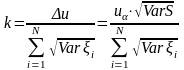 .
.
Следовательно,
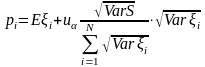 (18)
(18)
и
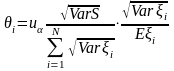 .
(18')
.
(18')
С точки зрения страховой компании все равно, какое из трех правил (13), (15) или (17) применять для начисления надбавок , так как в любом случае она получит одну и ту же страховую сумму
.
16. МОДЕЛИ ДОЛГОСРОЧНОГО СТРАХОВАНИЯ ЖИЗНИ
Долгосрочное страхование жизни, в отличие от краткосрочного страхования, характеризуется тем, что при расчетах принимают во внимание изменение стоимости денег с течением времени. Годовая процентная ставка, используемая при этом, носит название технической процентной ставки или технического процента. Технический процент выбирается страховщиком в таком размере, чтобы при самых неблагоприятных обстоятельствах обеспечить выбранную доходность инвестиций. Поэтому теория долгосрочного страхования существенно опирается на методы расчетов, рассматриваемых в финансовой математике.
Общую модель страхования определяют две функции:
а)
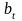 - величина страхового пособия,
выплачиваемого в момент времени
наступления страхового случая;
- величина страхового пособия,
выплачиваемого в момент времени
наступления страхового случая;
б)
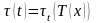 - момент выплаты страхового пособия –
функция остаточного времени жизни
застрахованного.
- момент выплаты страхового пособия –
функция остаточного времени жизни
застрахованного.
Величину страхового взноса с единицы страховой суммы называют тарифной ставкой или тарифом.
.
Непрерывное страхование жизни
1. Полное страхование жизни
фиксированное
страховое пособие
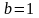 у.е. выплачивается в момент смерти,
поэтому
у.е. выплачивается в момент смерти,
поэтому
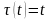 ,
,
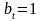 .
(1)
.
(1)
Этот вид страхования называют еще пожизненным страхованием на случай смерти.
2. п-летнее чисто накопительное страхование жизни
выплата страхового
пособия
производится в момент времени n,
если застрахованный дожил до этого
момента, и
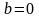 ,
если застрахованный умер до момента n,
то есть:
,
если застрахованный умер до момента n,
то есть:
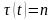 ,
,
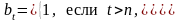 (2)
(2)
Этот вид страхования называют еще страхованием на чистое дожитие.
3. п-летнее временное страхование жизни
страхования сумма выплачивается, если застрахованный умер в течение срока действия договора, а если он прожил эти n лет, то страховая компания не платит ничего, то есть
,
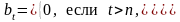 (3)
(3)
4. п-летнее смешанное страхование жизни
страховая сумма выплачивается или в момент смерти застрахованного, если это произошло до истечения срока действия договора, или выплачивается в момент окончания срока действия договора, то есть
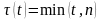 ,
.
(4)
,
.
(4)
этот вид страхования выполняет функции как собственно страхования, так и накопления средств.
Этот вид страхование называют еще страхованием на дожитие.
5. Полное страхование жизни, отсроченное на т лет
выплата страховой
суммы производится в момент смерти
застрахованного, но только в том случае,
если смерть произошла по истечении
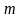 -летнего
срока, то есть
-летнего
срока, то есть
,
 (5)
(5)
можно вывести и другие виды отсроченного страхования, например, n - летнее временное страхование, отсроченное на m лет, то есть
,
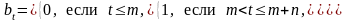 (6)
(6)
6. Страхование с переменной страховой выплатой
Существуют многочисленные виды страхования, в которых величина страхового пособия зависит от момента наступления страхового события, то есть меняется с течением времени. В простейшем варианте полного страхования жизни это будет выглядеть как стандартное возрастающее пожизненное страхование:
,
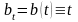 .
(7)
.
(7)
Страхование с выплатой страхового пособия в конце года смерти
Здесь речь идет о
дискретных
аналогах,когда
выплата пособия производится в конце
года смерти застрахованного, то есть в
момент времени
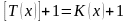 .
Тогда, для:
.
Тогда, для:
а) дискретного полного страхования жизни:
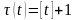 ,
;
(1´)
,
;
(1´)
б)
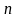 -
летнего дискретного временного
страхования жизни:
-
летнего дискретного временного
страхования жизни:
,
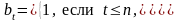 (3´)
(3´)
в) - летнего дискретного смешанного страхования жизни:
 ,
;
(4´)
,
;
(4´)
г) полного дискретного страхования жизни, отсроченного на лет:
, (5´)
д) полного страхования жизни с переменной страховой выплатой, например, с ежегодно возрастающим пособием
,
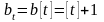 .
(7´)
.
(7´)
17. Принципы назначения нетто-премий. Полное страхование жизни.
Актуарная стоимость страховой выплаты
Современная стоимость (на момент заключения договора страхования) страховой выплаты будет определяться как
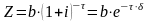 ,
,
где
- сложная процентная ставка,
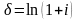 - сила роста (непрерывная процентная
ставка),
- сила роста (непрерывная процентная
ставка),
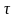 - момент выплаты страховой суммы.
- момент выплаты страховой суммы.
Так как является случайной величиной, то разовая нетто-премия равна ее актуарной стоимости, а именно
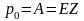 ,
(8)
,
(8)
где
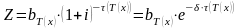 .
(9)
.
(9)
Для конкретных
видов страхования общая формула (9) может
быть упрощена и конкретизирована, и
современная стоимость
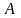 может быть выражена через характеристики
продолжительности жизни
может быть выражена через характеристики
продолжительности жизни
Для того, чтобы подчеркнуть, что речь идет о конкретных страховых договорах, переменные и снабжаются различными индексами, согласно следующим правилам:
Справа внизу ставится возраст х застрахованного на момент заключения договора:
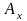 .
.Если договор страхования непрерывный, то есть, страховое пособие выплачивается в момент смерти, то сверху ставится черта:
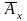 .
.Если договор действует ограниченный период времени n, то после возраста x через двоеточие ставится дополнительный индекс , обрамленный уголком:
 .
.Если договор отсрочен на m лет, то внизу слева ставится индекс
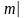 :
:
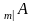 .
.Если величина страхового пособия регулярно возрастает, то добавляется буква
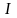 :
:
 .
.Используется также индекс 1 справа сверху. Например,
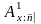 означает,
что первым наступил страховой случай
– смерть застрахованного в момент
времени
означает,
что первым наступил страховой случай
– смерть застрахованного в момент
времени
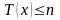 ;
а
;
а
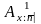 означает, что застрахованный умер не
ранее, чем через n
лет с момента заключения договора
страхования, и страховой случай наступил
в момент времени
означает, что застрахованный умер не
ранее, чем через n
лет с момента заключения договора
страхования, и страховой случай наступил
в момент времени
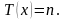
Полное страхование жизни
Согласно формулам
(1) и (9) получаем
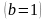 :
:
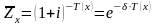 ,
(10)
,
(10)
и нетто-премия будет равна математическому ожиданию
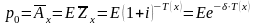 .
.
Обозначив
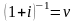 ,
можем получить:
,
можем получить:
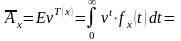
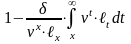 .
.
А если ввести обозначение:
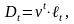 (11)
(11)
то
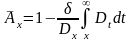 .
.
Функцию
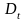 называют замещающей или упрощающей,
используется также и термин –
коммутационная
функция.
называют замещающей или упрощающей,
используется также и термин –
коммутационная
функция.
