1.Функция выживания.Кривая смертей.

в качестве первичной характеристики продолжительности жизни применяют функцию выживания

, (1)

она определяет вероятность того, что случайная величина X принимает значения, большие x, то есть случайно взятый человек уже прожил, по крайней мере, лет.

свойства функции выживания:

1) ,

2) ,

3) - непрерывная и строго убывающая функция.

Статистическим аналогом функции выживания s(x) является величина , равная среднему числу лиц, доживших до x лет:

, (2)

где l₀ - количество новорожденных человек. Тогда

характеризует среднюю долю живых представителей некоторой фиксированной группы новорожденных к моменту времени x.

Еще одной характеристикой продолжительности жизни служит плотность распределения вероятностей , определяемая как:

. (3)

Статистическим аналогом плотности распределения служит величина - число представителей исходной группы, умерших в возрасте от x до лет, а именно:

.

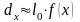Таким образом, плотность распределения вероятностей

(4)

она приближенно описывает долю умерших в возрасте от x до x+1 лет от исходной группы в новорожденных.

График функции (или ) называют кривой смертей.

свойства функции f (x):

1. .

2. ,

3. .

Таким образом, кроме и плотность распределения вероятностей может быть использована в качестве первичной характеристики продолжительности жизни, так как с помощью можно вычислить функцию выживания .

2.Интенсивность смерти.Макрохарактеристики продолжительности жизни.

интенсивность смертности- это величина, которая характеризует вероятность смерти в интервале человека, дожившего до x лет:

. (5)

Статистическим аналогом интенсивности смертности , является величина

,

характеризующая долю тех представителей исходной группы, доживших до возраста x лет, которые умрут в течение ближайшего года.

Для случайной величины определяют и такие числовые характеристики как математическое ожидание и дисперсия , которые можно вычислить по формулам:

,

.

Для работы со случайной величиной страховщики должны располагать показателями, которые позволяют им оценить риск смерти или дожития до определенного срока для лиц различного пола и возраста. Основной источник - таблицы смертности, которые составляются в каждой стране с определенной периодичностью на основе информации, собираемой в результате переписи населения.

В Приложении приведена общая или упрощенная таблица продолжительности жизни (aggregate tables), которая содержит информацию о статистических свойствах времени жизни случайно выбранного человека, относительно которого известен только его возраст.

В таблицу включены следующие характеристики:

а) - среднее число живых представителей некоторой группы из новорожденных к возрасту x лет;

б) - число представителей группы, умерших в возрасте от x до лет;

в) - доля тех представителей группы, доживших до возраста x лет, которые умрут в течение ближайшего года;

г) - среднее суммарное число лет, прожитых представителями группы в возрасте от x до лет;

д) - среднее суммарное число лет, прожитых представителями группы в возрасте от x лет и более;

е) - среднее остаточное время жизни.

В качестве шага таблицы рассматривается 1 год

Аналитический закон распределения-Де Муавр (1724 г.) постулировал существование максимального возраста для людей и предположил, что X подчиняется равномерному закону распределения вероятностей в интервале :

,

тогда

. (6)

3. . Распределение остаточного времени жизни. Основные величины, связанные с оста-

точным временем жизни

При страховании жизни страхователь имеет дело с конкретными людьми, дожившими до определенного возраста x. Поэтому необходимо рассмотрение случайной величины

, (7)

определяющей остаточное время жизни человека, дожившего до х лет.

Закон распределения вероятностей этой случайной - . В страховой математике обозначают как :

- (8)

вероятность смерти человека, достигшего возраста x лет, в течение ближайших t лет.

Дополнительная вероятность обозначается как :

-

это вероятность того, что человек в возрасте x лет проживет еще не менее лет.

В частном случае, при индекс опускают:

вероятность того, что человек в возрасте х лет умрет в течение ближайшего года, и

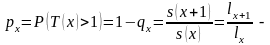
вероятность того, что человек в возрасте х лет проживет, по крайней мере, еще один год.

Через эти характеристики можно выразить и вероятности :

;

Рассматривается также и вероятность

того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении последующих u лет. Эта вероятность будет вычисляться как

или

Учитывая формулу (8) можем получить:

(9)

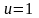Если , то

-

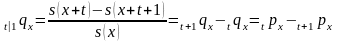вероятность того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении следующего года.

4.Числовые характеристики остаточного времени жизни.Частичная очтаточная продолжительность жизни.

При страховании жизни страхователь имеет дело с конкретными людьми, дожившими до определенного возраста x. Поэтому необходимо рассмотрение случайной величины

, (7)

определяющей остаточное время жизни человека, дожившего до х лет.

Закон распределения вероятностей этой случайной - . В страховой математике обозначают как :

- (8)

вероятность смерти человека, достигшего возраста x лет, в течение ближайших t лет.

Дополнительная вероятность обозначается как :

-

это вероятность того, что человек в возрасте x лет проживет еще не менее лет.

В частном случае, при индекс опускают:

вероятность того, что человек в возрасте х лет умрет в течение ближайшего года, и

вероятность того, что человек в возрасте х лет проживет, по крайней мере, еще один год.

Через эти характеристики можно выразить и вероятности :

;

Рассматривается также и вероятность

того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении последующих u лет. Эта вероятность будет вычисляться как

или

Учитывая формулу (8) можем получить:

(9)

Если , то

-

вероятность того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении следующего года.

5.Закон распределения вероятностей округленного времени жизни.Числовые характеристики округленного времени жизни.

В связи с тем, что обычно страховые компании заключают договора страхования жизни на целое число лет, возникает необходимость наряду с остаточным временем жизни T(x) рассмотреть и её целую часть 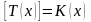– округленную остаточную продолжительность жизни.

Округленная остаточная продолжительность жизни является дискретной случайной величиной, принимающей возможные значения 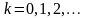, с соответствующими вероятностями .

Согласно определению имеем

,

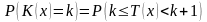- (10)

это и есть закон распределения вероятностей дискретной случайной величины .

Рассмотрим теперь задачу определения закона распределения для дробных возрастов , которая решается с помощью интерполяции. Для этого рассмотрим несколько интерполяционных методов определения функции выживания , с помощью которой и определяется закон распределения .