
Численные методы
Задание 1
Интерполяционный
многочлен Лагранжа второй степени
![]() ,
составленный по таблице значений функции
,
составленный по таблице значений функции
![]() :
:
![]() имеет
вид …
Варианты ответа
имеет
вид …
Варианты ответа
Решение:
Интерполяционный
многочлен Лагранжа 2-ой степени для
таблицы
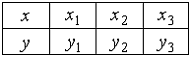 имеет
вид
имеет
вид
 В
нашем случае
В
нашем случае
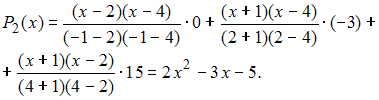
Задание 2
Значение
![]() с
использованием приближенной формулы
с
использованием приближенной формулы
![]() с
точностью до 0,01 равно …
Варианты
ответа
с
точностью до 0,01 равно …
Варианты
ответа
4,02
4,13
4,09
4,08
Решение:
Воспользуемся
приближенной формулой
.
В
нашем случае
![]() ,
,
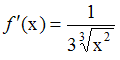 ,
,
![]() ,
,
![]() и
и
![]() Получаем
Получаем
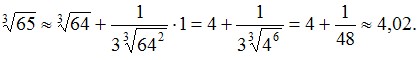
Задание 3
Если
методом Эйлера с шагом
![]() решать
задачу Коши
решать
задачу Коши
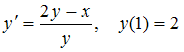 ,
то значение
,
то значение
![]() искомой
функции будет равно …
искомой
функции будет равно …
Задание 4
Значение
интеграла
 ,
вычисленное с помощью рядов с точностью
до 0,01, равно …
,
вычисленное с помощью рядов с точностью
до 0,01, равно …
Задание 5
Если методом Эйлера с шагом решать задачу Коши , то значение искомой функции будет равно …
Задание 6
Функция
![]() представлена
таблицей
представлена
таблицей
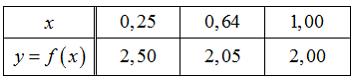 Методом
кусочно-линейной интерполяции находится
значение
Методом
кусочно-линейной интерполяции находится
значение
![]() ,
где
,
где
![]() .
Известно, что на отрезке
.
Известно, что на отрезке
![]() производная
2-го порядка заданной функции имеет
максимальное (по модулю) значение, равное
22.
Тогда погрешность вычисления
значения
не
превышает …
производная
2-го порядка заданной функции имеет
максимальное (по модулю) значение, равное
22.
Тогда погрешность вычисления
значения
не
превышает …
Задание 7
Интеграл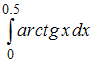 вычисляется при помощи разложения
подынтегральной функции в степенной
ряд. Тогда его значение с точностью
0,001 равно …
вычисляется при помощи разложения
подынтегральной функции в степенной
ряд. Тогда его значение с точностью
0,001 равно …
Задание 9
Пусть
–
алгебраическая или трансцендентная
функция:
1) определённая на отрезке
![]() ,
2) имеющая на отрезке
непрерывные
производные
,
2) имеющая на отрезке
непрерывные
производные
![]() и
и
![]() ,
сохраняющие знак на этом отрезке,
3)
имеющая единственный корень
,
сохраняющие знак на этом отрезке,
3)
имеющая единственный корень
![]() на
отрезке
.
Этот
корень необходимо найти приближённо,
используя метод Ньютона (касательных).
Тогда
выбор начального приближения
на
отрезке
.
Этот
корень необходимо найти приближённо,
используя метод Ньютона (касательных).
Тогда
выбор начального приближения
![]() ,
вычисление приближений
,
вычисление приближений
![]() и
оценка погрешности осуществляются
соответственно по следующим формулам:
и
оценка погрешности осуществляются
соответственно по следующим формулам:
Задание 9
Для
функции
![]() известны
её значения в узлах
известны
её значения в узлах
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Требуется вычислить значение этой
функции в точке
.
Требуется вычислить значение этой
функции в точке
![]() .
Для
вычисления
.
Для
вычисления
![]() используется
интерполяционный полином Лагранжа
используется
интерполяционный полином Лагранжа
![]() 3-й
степени. Погрешностями округлений
пренебрегают.
Тогда величина
3-й
степени. Погрешностями округлений
пренебрегают.
Тогда величина
![]() не
превышает …
не
превышает …
Задание 10
Функция
представлена
таблицей
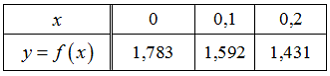 Известно,
что на отрезке
Известно,
что на отрезке
![]() максимальное
значение производной третьего порядка
максимальное
значение производной третьего порядка
![]() равно
12. В точке
равно
12. В точке
![]() вычислено
значение производной
вычислено
значение производной
![]() на
основе интерполяционного полинома
Лагранжа 2-й степени.
Тогда погрешность
(округлённая до двух знаков после
запятой) не превышает значения …
на
основе интерполяционного полинома
Лагранжа 2-й степени.
Тогда погрешность
(округлённая до двух знаков после
запятой) не превышает значения …
«Комплексный анализ»
Модуль комплексного числа
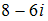 равен
…
равен
…
Варианты ответа
10
14
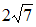
2
Решение:
Если
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() .
.
Задание 2
Если
![]() и
и
![]() ,
то сумма
,
то сумма
![]() равна
…
Варианты ответа
равна
…
Варианты ответа
7
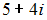
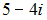
5
Решение:
Указанная
сумма находится следующим образом:
![]() .
.
Задание 3
Все
точки
![]() комплексной
плоскости, принадлежащие множеству D
, изображённому на рисунке,
комплексной
плоскости, принадлежащие множеству D
, изображённому на рисунке,
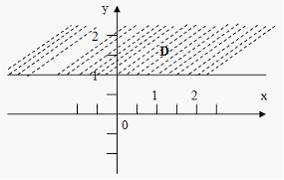 удовлетворяют
условию …
удовлетворяют
условию …
Задание 4
Дана
функция
 .
Тогда
.
Тогда
![]() равно
…
равно
…
Задание 5
Комплексное
число, сопряженное числу
![]() ,
имеет вид …
,
имеет вид …
Задание 6
Значение
выражения
![]() равно
…
равно
…
Задание 7
Мнимая
часть функции
![]() ,
где
,
где
![]() ,
имеет вид …
,
имеет вид …
Задание 8
Разностью
множеств
![]() и
и
![]() может
являться множество …
может
являться множество …
Задание 9
Мера
плоского множества, изображенного на
рисунке,
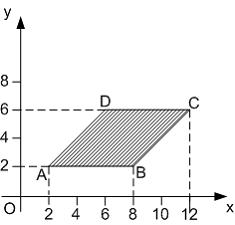 в
пространстве
в
пространстве
![]() равна
…
равна
…
Задание 10
Образом
интервала
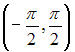 при
отображении
при
отображении
![]() является
множество …
является
множество …
Задание 11
Множество
упорядоченных пар действительных чисел
![]() с
расстоянием
с
расстоянием
 образует
метрическое пространство …
образует
метрическое пространство …
Задание 12
Мера
плоского множества, изображенного на
рисунке,
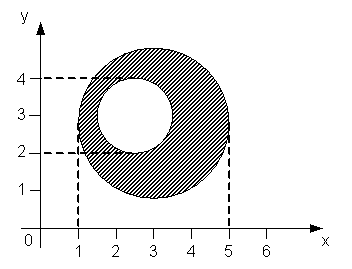 в
пространстве
в
пространстве
![]() равна
…
равна
…
Задача 13
Отображение
отрезка
![]() на
отрезок
на
отрезок
![]() может
быть задано функцией …
может
быть задано функцией …
Задание 14
Дано
множество
![]() с
метрикой
с
метрикой
![]() ,
где
,
где ![]() и
и
![]() .
Тогда
областью, соответствующей неравенству
.
Тогда
областью, соответствующей неравенству
![]() ,
где
,
где
![]() –
начало координат, является …
–
начало координат, является …
Задание 15
Среди указанных множеств замкнутым является…
Задание 16
Из представленных метрических пространств полным не является пространство…
Задание 17
Для
произвольного метрического пространства
![]() отображение
отображение
![]() называется
сжимающим, если…
называется
сжимающим, если…
Функциональный анализ
Задание 18
Разность двух измеримых функций есть функция …
Задание 19
В
произвольном метрическом пространстве
последовательность
![]() называется
фундаментальной, если…
называется
фундаментальной, если…
Задание 20
Пусть
множество D
на декартовой плоскости состоит из всех
точек (x;y) круга
![]() .
Тогда сжимающим отображением для D
будет отображение
.
Тогда сжимающим отображением для D
будет отображение
![]() ,
заданное соотношением …
,
заданное соотношением …
Задание 21
Функция
![]() ,
принимающая значения на
,
принимающая значения на
![]() ,
называется
,
называется
![]() -измеримой,
если из условия
-измеримой,
если из условия
![]() вытекает,
что …
вытекает,
что …
Задание 23
Для
произвольного метрического пространства
сходимость последовательности
к
пределу
![]() может
быть определена так:
может
быть определена так:
Задание 24
Из
указанных метрических пространств:![]() –
множество всех непрерывных действительных
функций, определенных на отрезке
–
множество всех непрерывных действительных
функций, определенных на отрезке
![]() с
расстоянием
с
расстоянием
![]() ;
;
![]() –
пространство, точками которого служат
всевозможные последовательности
–
пространство, точками которого служат
всевозможные последовательности
![]() действительных
чисел, удовлетворяющие условию
действительных
чисел, удовлетворяющие условию
 ,
а расстояние определяется формулой
,
а расстояние определяется формулой
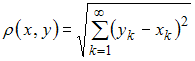 ;
;
![]() –
множество всех непрерывно дифференцируемых
действительных функций, определенных
на отрезке
с
расстоянием
–
множество всех непрерывно дифференцируемых
действительных функций, определенных
на отрезке
с
расстоянием
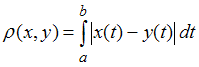 ;
;
![]() –
множество упорядоченных групп из n
действительных чисел
с
расстоянием
,
–полным не является …
–
множество упорядоченных групп из n
действительных чисел
с
расстоянием
,
–полным не является …
