
Математическая статистика
Задание 1
Медиана вариационного ряда 12, 13, 14, 16, 17, 17, 19 равна … Варианты ответа
7
16
15,5
17
Решение:
Медианой вариационного ряда называется значение признака генеральной совокупности, приходящееся на середину вариационного ряда. В данном случае – это варианта, расположенная в середине вариационного ряда. В середине данного ряда располагается варианта 16.
Задание 2
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 8, 10, 11, 13, 16. Тогда несмещенная оценка математического ожидания равна … Варианты ответа
12,0
11,6
11,4
11,0
Решение:
Несмещенная
оценка математического ожидания
вычисляется по формуле:
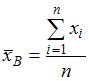 .
То есть
.
То есть
![]() .
.
Задание 3
Точечная оценка математического ожидания нормально распределенного количественного признака равна 15. Тогда его интервальная оценка может иметь вид …
Задача 4
Левосторонняя критическая область может определяться из соотношения …
Задание 5
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 4,5; 5,5; 6,5. Тогда несмещенная оценка дисперсии равна …
Задание 6
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
Задание 7
Левосторонняя критическая область может определяться из соотношения …
Задание 8
Из
генеральной совокупности извлечена
выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
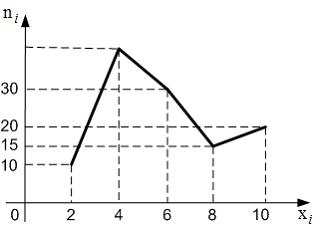 Тогда
относительная частота варианты
Тогда
относительная частота варианты ![]() в
выборке равна …
в
выборке равна …
Задание 9
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
несмещенная оценка математического
ожидания равна …
Тогда
несмещенная оценка математического
ожидания равна …
Задание 10
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
Задание 11
Выборочное
уравнение парной регрессии имеет вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
Задание 12
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
значение
Тогда
значение
![]() равно
…
равно
…
Задание 13
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 12,5; 14,5; 16,5. Тогда несмещенная оценка дисперсии равна …
Задание 14
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
Задание 15
При
построении выборочного уравнения парной
регрессии вычислены: выборочный
коэффициент корреляции
![]() и
выборочные средние квадратические
отклонения
и
выборочные средние квадратические
отклонения
![]() .
Тогда выборочный коэффициент регрессии
Y
на X
равен …
.
Тогда выборочный коэффициент регрессии
Y
на X
равен …
Задание 16
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
относительная частота варианты
Тогда
относительная частота варианты
![]() равна
…
равна
…
Задание 17
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 21,3; 24,3; 27,3. Тогда несмещенная оценка дисперсии равна …
Задание 18
Выборочное
уравнение парной регрессии имеет вид
![]() ,
а выборочные средние квадратические
отклонения равны:
,
а выборочные средние квадратические
отклонения равны:
![]() .
Тогда выборочный коэффициент корреляции
.
Тогда выборочный коэффициент корреляции
![]() равен
…
равен
…
Задание 19
Соотношением
вида
![]() можно
определить …
можно
определить …
Задание 20
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
несмещенная оценка математического
ожидания равна …
Тогда
несмещенная оценка математического
ожидания равна …
Задание 21
Выборочное
уравнение парной регрессии имеет вид
![]() .
Тогда выборочный коэффициент регрессии
равен …
.
Тогда выборочный коэффициент регрессии
равен …
Задание 22
Соотношением вида можно определить …
«РЯДЫ»
Задание 1
Общий
член числовой последовательности
![]() и
и
![]() .
Тогда
.
Тогда
![]() равно
…
Варианты ответа
равно
…
Варианты ответа
2
4
6
0,25
Решение:
Из
соотношения
последовательно
вычисляем:
![]()
![]()
Задание 2
Даны
числовые ряды:
A)
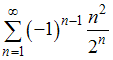 B)
B)
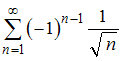 C)
C)
 D)
D)
 .
Тогда
абсолютно сходящимся рядом является
ряд …
Варианты ответа
.
Тогда
абсолютно сходящимся рядом является
ряд …
Варианты ответа
A
B
C
D
Решение:
Рассмотрим
ряд
,
который является знакопеременным. Для
исследования ряда на сходимость применим
признак Даламбера.
Пусть
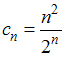 ,
тогда имеем для последовательности
Даламбера
,
тогда имеем для последовательности
Даламбера
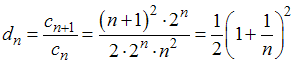 и
и
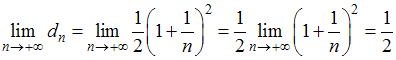 .
А
т.к.
.
А
т.к.
![]() ,
то по признаку Даламбера исследуемый
ряд сходится абсолютно.
Поскольку
ряд
,
то по признаку Даламбера исследуемый
ряд сходится абсолютно.
Поскольку
ряд
 расходится
(расходящийся обобщённый гармонический
ряд), то ряд
не
является абсолютно сходящимся рядом.
Ряд
расходится
(расходящийся обобщённый гармонический
ряд), то ряд
не
является абсолютно сходящимся рядом.
Ряд
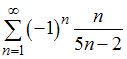 расходится,
т.к. для него не выполняется необходимое
условие сходимости:
расходится,
т.к. для него не выполняется необходимое
условие сходимости:
![]() не
существует.
Для ряда
имеем
не
существует.
Для ряда
имеем
![]() ,
а ряд
,
а ряд
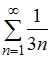 расходится
(это, по сути дела, гармонический ряд),
тогда заданный ряд не является абсолютно
сходящимся (но сходится условно).
Итак,
абсолютно сходящимся рядом является
ряд
.
расходится
(это, по сути дела, гармонический ряд),
тогда заданный ряд не является абсолютно
сходящимся (но сходится условно).
Итак,
абсолютно сходящимся рядом является
ряд
.
Задание 3
Если
радиус сходимости степенного ряда
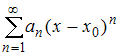 равен
R,
то интервал сходимости этого ряда имеет
вид …
равен
R,
то интервал сходимости этого ряда имеет
вид …
Задание 4
Рядом
Маклорена для функции
![]() является
…
является
…
Задание 5
Ряд
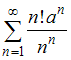 расходится
при наименьшем целом положительном
значении параметра
расходится
при наименьшем целом положительном
значении параметра
![]() ,
равном …
,
равном …
Задание 6
Если радиус сходимости степенного ряда равен R, то интервал сходимости этого ряда имеет вид …
Задание 8
Предел
числовой последовательности
 при
при
![]() равен
…
равен
…
Задание 8
Даны
числовые ряды:
A)
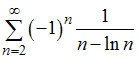 B)
B)
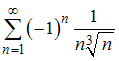 C)
C)
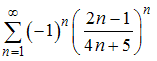 D)
D)
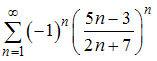 Тогда
условно сходится ряд …
Тогда
условно сходится ряд …
Задание 9
Радиус
сходимости степенного ряда
 равен
…
равен
…
Задание 10
Из
числовых последовательностей
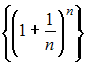 ,
,
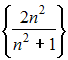 ,
,
![]() ,
,
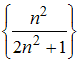 наибольшее
значение предела при
наибольшее
значение предела при
![]() имеет
последовательность …
имеет
последовательность …
Задание 11
Из
рядов
![]() ,
,
![]() ,
,
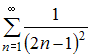 ,
,
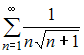 расходящимся
является ряд …
расходящимся
является ряд …
Задача 12
Область
сходимости степенного ряда
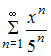 имеет
вид …
имеет
вид …
Задание 13
Из
последовательностей
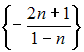 ,
,
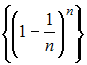 ,
,
![]() ,
,
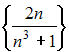 наименьшее
значение предела при
имеет
последовательность …
наименьшее
значение предела при
имеет
последовательность …
Задание 13
Для исследования сходимости или расходимости признак Даламбера не применим к ряду …
Задание 14
Даны
ряды:
1)
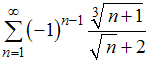 ;
2)
;
2)
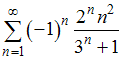 .
Тогда
справедливо утверждение: …
.
Тогда
справедливо утверждение: …
Задание 15
Последовательность
![]() задана
рекуррентным соотношением
задана
рекуррентным соотношением
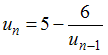 ,
,
![]() ,
,
![]() .
Тогда
предел при
этой
последовательности равен …
.
Тогда
предел при
этой
последовательности равен …
Задание 16
Признак Коши не применим для установления сходимости или расходимости ряда …
