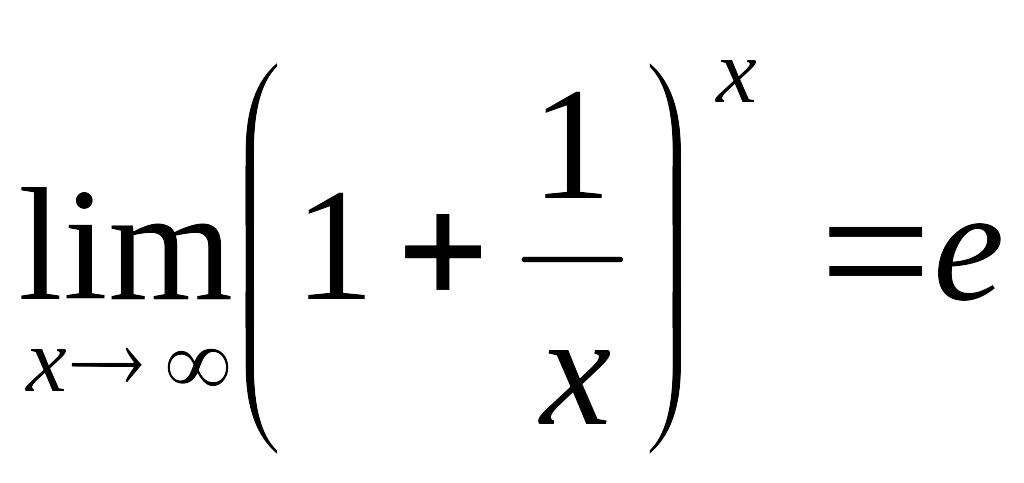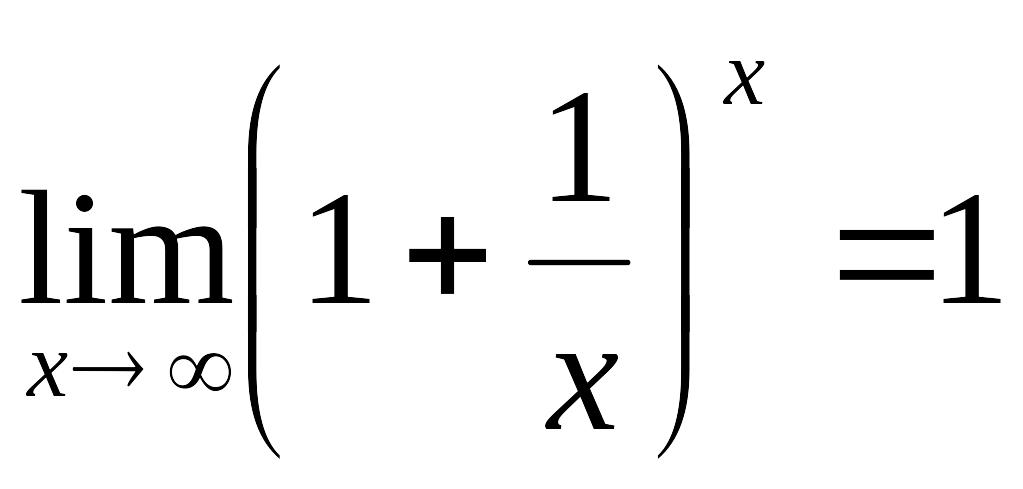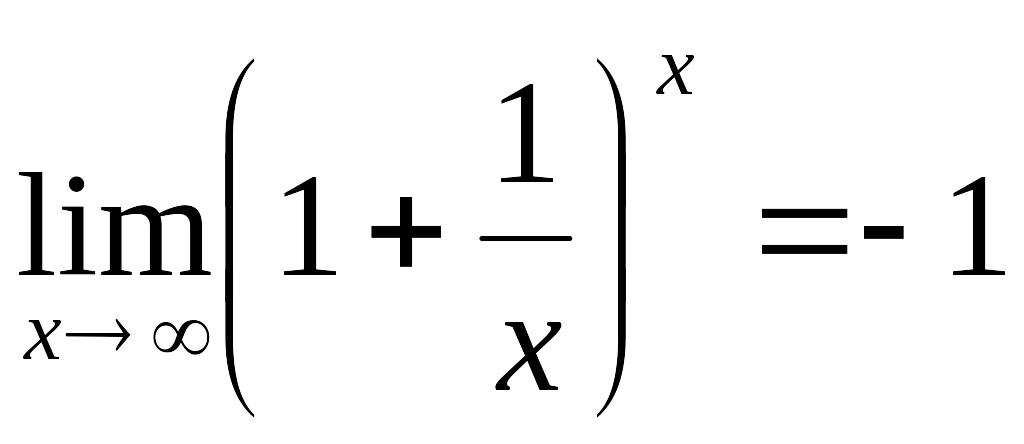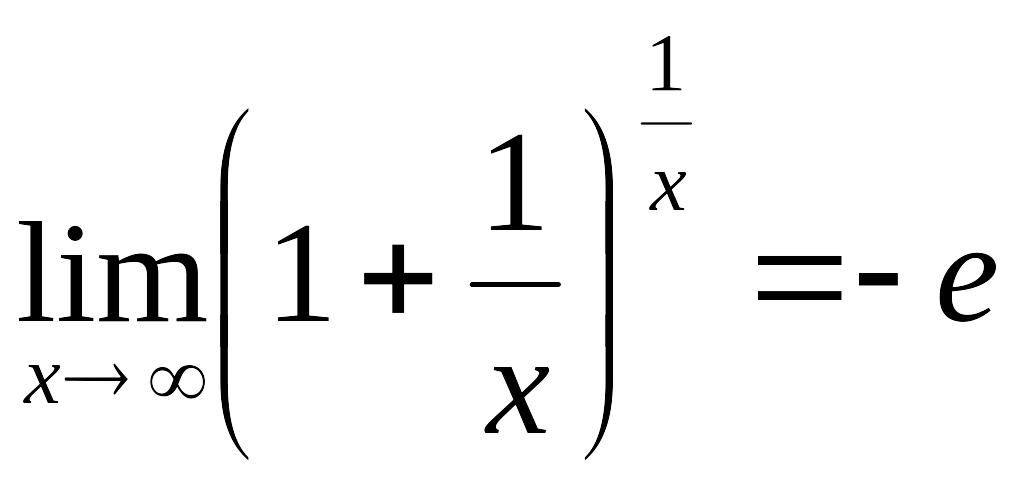3. Уравнение плоскости, проходящей через ось Оz

4. уравнение плоскости, проходящей через ось Оx

5. уравнение плоскости, перпендикулярной оси Оz

0323 Условие совпадения плоскостей и :

1. 

2. A₁А₂+B₁В₂+C₁С₂=0

3. A₁А₂+B₁В₂+C₁С₂=1

4. A₁(x-x₀)+B₁(y-y₀)+C₂(z-z₀)=0

0324 Условие совпадения прямых и :

1. 

2. A₁А₂+B₁В₂+D₁D₂=0

3. A₁А₂+B₁В₂+ D₁D₂=1

4. A₁(x-x₀)+B₁(y-y₀)+D₁(z-z₀)=0

5. 

0325 Уравнение Ax + By + Cz + D = 0 с тремя неизвестными, при А=С=0 определяет:

1. уравнение прямой

2. уравнение плоскости, проходящей через начало координат

3. уравнение плоскости параллельной плоскости xOy

4. Уравнение плоскости, параллельной плоскости xOz

5. уравнение плоскости, параллельной плоскости yOz

Раздел 4

0401 Бесконечно малые функции и при называются эквивалентными, если:

1. 

2. 

3. 

4. 

5. 

0402 Указать формулу интегрирования по частям для неопределенного интеграла:

1. 

2. 

3. 

4. 

5. 

0403 Из сходимости последовательности следует, чтоона:

1. ограничена

2. не ограничена

3. убывающая

4. монотонна

5. возрастающая

0404 Интеграл равен:

1. 

2. 1

3. 0

4. F(x)

5. 

0405 Функция называется первообразной для функции на промежутке , если:

1. 

2. 

3. 

4. 

5. 

0406 Функция интегрируема на отрезке , если она на этом отрезке:

1. непрерывная

2. убывающая

3. возрастающая

4. ограничена

5. неограничена

0407 =?

2. 

3. 1

4. 

5. 

0408 Указать неверное равенство для неопределенного интеграла:

1. 

2. 

3. 

4. 

5. 

0409 Указать первый замечательный предел:

1. 

2. 

3. 

4. 

5. 

0410 Указать второй замечательный предел:

1. 

2. 

3. 

4. 

5. 

0411 Указать формулу Ньютона-Лейбница:

1. 

2. 

3. 

4. 

5. 

0412 Если производная дифференцируемой функции положительна внутри некоторого промежутка, то:

1. функция не постоянна

2. функция убывает на этом промежутке

3. функция постоянна на этом промежутке

4. функция возрастает на этом промежутке

5. функция положительна на этом промежутке

0413 Если производная от функции всюду в интервале отрицательна, то функция в этом интервале:

1. равна нулю

2. возрастает

3. постоянна

4. убывает

5. имеет экстремум

0414 Если функция - четная, то опеределенный интеграл

равен:

1. 

2. 0

3. 1

4. 

5. 

0415 Если функция дифференцируема в точке и имеет в этой точке локальный экстремум, то:

1. 

2. 

3. 

4. 

5. 

0416 Производная функции в точке обозначается и определяется как:

1. 

2. 

3. 

4. 

5. 

0417 Если функция - нечетная, то определенный интеграл

равен:

1. 0

3. 1

0418 Неопределенный интеграл равен:

1. ,

2. ,

3. ,

4. 

5. ,

0419

1. 

2. 

3. 

4. 

5. 

0420 Уравнение касательной к графику функции в точке имеет вид:

1. 

2. 

3. 

4. 

5. 

0421 Уравнение нормали к графику функции в точке имеет вид:

5. 

0422 Если график функции выпуклый на интервале (a,b) и на этом интервале существует f^//(x),

то на этом интервале:

1. f^//(x)=0

2. f^//(x)>0

3. f^//(x)<0

4. f^//(x) 1

5. f^//(x) 0

0423 Если график функции вогнутый на интервале (a,b) и на этом интервале существует f^//(x),

то на этом интервале:

1. f^//(x)>0

2. f^//(x)=0

3. f^//(x)<0

4. f^//(x) 1

5. f^//(x) 1

0424 Пусть функция дважды дифференцируема в точке и .

Тогда функция имеет в точке локальный максимум, если:

1. 

2. 

3. 

4. 

5. 

0425 Пусть функция дважды дифференцируема в точке и .

Тогда функция имеет в точке локальный минимум, если:

4. 

5.