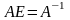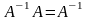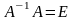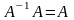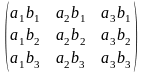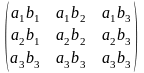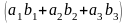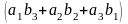- •Раздел 1
- •Нет правильного ответа
- •Нет правильного ответа
- •Раздел 2
- •Больше единицы
- •Меньше единицы
- •Коллинеарные
- •Раздел 3
- •Каноническими уравнениями прямой
- •Уравнение плоскости
- •Общим уравнением прямой
- •Уравнение плоскости, проходящей через начало координат
- •Уравнение плоскости, проходящей через ось Оz
- •Уравнение плоскости, параллельной плоскости xOz
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Раздел 7
- •Раздел 8
- •Раздел 9
- •Раздел 10
- •Раздел 11
- •Раздел 12
- •Раздел 13
- •Раздел 14
- •Раздел 15
- •Раздел 16
- •Раздел 17
- •Раздел 18
- •Раздел 19
- •Раздел 20
Раздел 1
0101 Минором Мij элемента аij определителя порядка n называется:
число, равное произведению диагональных элементов
матрица (n-1)-го порядка, полученная путем вычеркивания i-ой строки и j-го столбца
определитель (n-1)-го порядка, полученный из определителя порядка n путем вычеркивания i-ой строки и j-го столбца
определитель (n-1)-го порядка, полученный из определителя порядка n путем вычеркивания i-ой строки и j-го столбца, взятый со знаком (-1)i+j
определитель (n-1)-го порядка, полученный из определителя порядка n путем вычеркивания j-ой строки и i-го столбца со знаком (-1)i+j
0102 Квадратная матрица A называется вырожденной (особенной), если:
А·А-1= Е
А 0
А = 0
А·А-1 Е
А = 1
0103 Пусть А – матрица коэффициентов при неизвестных системы линейных уравнений, B - расширенная матрица системы. Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы:
rang A > rang B
rang A < rang B
rang A = rang B
rang A rang B
rang A – rang B=-1
0104 Пусть А – матрица системы линейных однородных уравнений. Если А ≠ 0, то система:
имеет множество решений
имеет одно решение
либо имеет множество решений, либо не имеет решений
имеет одно не тривиальное решение
не имеет решений
0105 Пусть А – матрица коэффициентов системы линейных уравнений. Система линейных уравнений называется определенной, если:
система имеет множество решений
система имеет одно решение
А = 0
система либо имеет множество решений, либо не имеет решений
система не имеет решений
0106 Обратной
матрицей
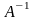 к матрице
к матрице
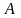 называется такая матрица, которая
удовлетворяет равенству (
называется такая матрица, которая
удовлетворяет равенству ( -
единичная матрица):
-
единичная матрица):
0107 Единичной матрицей называется:
прямоугольная матрица, все элементы которой являются единицами
квадратная матрица, все элементы которой являются единицами
квадратная матрица, определитель которой равен единице
квадратная матрица, у которой элементы главной диагонали единицы, а остальные элементы – нули
квадратная матрица, у которой элементы побочной диагонали - единицы, а остальные элементы – нули
0108 Укажите верное выражение для алгебраического дополнения:
Aij=-Mij
Aij=Mij
Aij=(-1)i+jMij
Aij=(-1)iMij
Aij=(-1)jMij
0109 Если два параллельных ряда определителя равны, то определитель:
больше нуля
меньше нуля
равен нулю
не вычислим
нет правильного ответа
0110 Пусть А – матрица системы линейных неоднородных уравнений. Если А ≠ 0, то система:
имеет множество решений
имеет одно решение
либо имеет множество решений, либо не имеет решений
имеет только тривиальное решение
не имеет решений
0111 Система трех линейных неоднородных уравнений либо не имеет решений, либо имеет бесчисленное множество решений, если определитель матрицы этой системы:
равен нулю
не равен нулю
равен единице
больше единицы
меньше единицы
0112 Система трех линейных уравнений с тремя неизвестными не имеет единственного решения тогда и только тогда, когда определитель матрицы этой системы:
не равен нулю
равен нулю
равен единице
больше единицы
меньше единицы
0113 Однородная система трех линейных уравнений с тремя неизвестными имеет ненулевые решения, если определитель матрицы этой системы:
равен нулю
не равен нулю
равен единице
больше единицы
меньше единицы
0114 Укажите размерность матриц А и В, для которых возможно найти произведение:
A(3
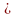 1)·B(1
2)
1)·B(1
2)
A(3 1)·B(2 3)
A(3 1)·B(3 2)
A(2 3)·B(2 3)
A(1 3)·B(1 2)
0115 Записать матрицу, полученную в результате умножения следующих матриц:

0116 Минором элемента а23 определителя является:
определитель, который находится по формуле M23=(-1)2+3A23
определитель, который находится по формуле M23=(-1)2+3A32
определитель, который получается из данного вычёркиванием 2 строки и 3 столбца
определитель, который получается из данного вычёркиванием 3 строки и 2 столбца
нет правильного ответа
0117 Если переставить местами два параллельных ряда определителя, то он:
не изменится
поменяет знак на противоположный
будет равен нулю
станет отрицательным числом
станет положительным числом
0118 При транспонировании квадратной матрицы её определитель:
не изменится
поменяет знак на противоположный
будет равен нулю
станет отрицательным числом
станет положительным числом
0119 Система линейных уравнений называется совместной, если она:
не имеет ни одного решения
имеет хотя бы одно решение
имеет тривиальное решение
имеет число уравнений равное числу неизвестных
имеет число уравнений не равное числу неизвестных
0120 Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы:
ранг матрицы системы был равен рангу расширенной матрицы
ранг матрицы системы был не равен рангу расширенной матрицы
ранг матрицы системы был больше ранга расширенной матрицы
ранг матрицы системы был меньше ранга расширенной матрицы
ранг матрицы системы был равен m
0121 Для матрицы
А=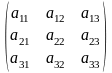 матрица А*
называется
присоединённой (союзной), если:
матрица А*
называется
присоединённой (союзной), если:
 =0
=0
А*=
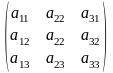
А*=
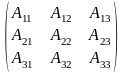
А*=

0122 Если матрица А – невырожденная, А*- её присоединённая матрица, то:
существует А-1=
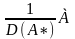
существует АТ=
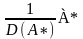
существует АТ=
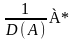
существует А-1=