2. Теорема об интегрировании оригинала.

Если ≒ ,

то ≒

т.е. интегрированию оригинала соответствует деление на изображения. Эта теорема используется обычно для отыскания оригинала по изображению.

а) ≓

Так как ≓ , ≓

≓

≒

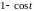
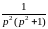б) ≓

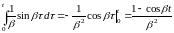
в) ≓ ?

Найдем оригинал ≓ 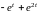, затем

≓

3. Теорема о дифференцировании изображения.

Если ≒ ,

то ≒

≒

а) ≒

≒ (формула была известна ранее)

Зная, что

б) ≒

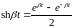≒ Аналогично выводится ≒

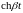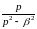
Найдем

≒

Или ≒

в) ≒

≒

≒ ;

4. Теорема об интегрировании изображения.

Если ≒ ,

то ≒

_а) ≒

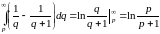
б) ≒

Если функцию нетрудно проинтегрировать, то иногда с помощью такого интеграла можно найти оригинал.

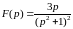1. - оригинал мы не знаем.

≓

Следовательно

≓

2. 

≓

Следовательно

≓

Решать все примеры не обязательно

1 час – решение уравнений,

2 час – теоремы (применение)

Можно дать на каждую теорему 2-3 примера. Если остается время остальные примеры предложить для самостоятельного решения.

На дом:

1. ,

Ответ:

2. ;

Ответ:

3. Найти изображения и оригиналы:

а) ≒

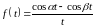б) ≒

в)

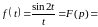
4. а) ≓

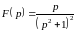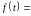
б) ≓

в) ≓

Занятие 3

1. Повторение прошлой темы.

Пример 1.

Решить линейное неоднородное дифференциальное уравнение:

.

Решение:

,

,

; ;

;

_.

.

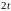
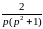
2. Теорема свертывания

(Возможно, что теорема была доказана на лекции не во всех группах)

Сверткой двух функций и называется функция

, оригинал, которой находится по формуле:

≒

(какую функцию назвать первой, а какую второй – безразлично)

Если ≒ , ≒ , то

≒

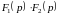
Пример 1.

Решить уравнение:

≓ ?

Решение:

; ≓ , ≓

≓

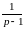≓ - формула была получена ранее

Пример 2.

Решить уравнение:

≓ ? ≓ , ≓

Решение:

≓

,

≓ - эта формула так же была получена на прошлом занятии.

Пример 3.

Решить уравнение:

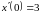
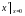
Решение:

≓

≒

≒ ≒

≓ , ≓ , ≓ ,

≓ =

≓

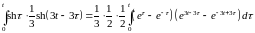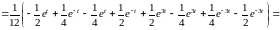
3. Теоремы разложения

Теоремы разложения применяются для нахождения оригинала , когда известно изображение . Каждая из этих теорем справедлива лишь при определенных частных условиях, накладываемых на изображение . Однако классы функций, удовлетворяющих этим условиям, являются весьма широкими; вычисления же, связанные с применением теорем разложения, настолько просты, что использование этих теорем при решении многих конкретных задач оказывается весьма эффективным.

Первая теорема разложения

Предположим, что данное изображение может быть разложено в ряд по степеням :

,

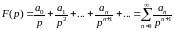сходящийся при .

Если к каждому отдельному члену этого ряда применить операционное соотношение:

,

то оригинал определяется формулой:

.

Пример 1.

разлагается в ряд:

По первой теореме разложения:

.