Практические занятия по курсу «операционное исчисление» Занятие 1

1. Преобразование Лапласа. Оригинал и изображение.

Пусть 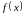- действительная функция действительного аргумента , которую будем интерпретировать как время.

Определение. Будем называть функцию оригиналом, если она удовлетворяет трем требованиям:

1. и ее производная на любом конечном интервале оси имеют не более конечного числа точек разрыва 1-го рода;

2. , при ;

3. существуют такие постоянные и , что для всех .

Условие а) означает, что оригинал является кусочно-гладкой функцией времени ; это значит, что любой конечный интервал оси можно разбить на конечное число таких интервалов, в каждом из которых и непрерывны и в концах этих интервалов имеют конечные левые и правые пределы. Большинство практически встречающихся функций этому условию удовлетворяют.

Условие б) оправдано тем, что для физики и техники совершенно безразлично, как ведут себя рассматриваемые функции до некоторого начального момента времени, который, разумеется, всегда можно принять за момент .

Условие в) накладывает ограничение на характер роста оригинала , а именно требует, чтобы при возрастала не быстрее показательной функции. Большинство функций, встречающихся на практике, удовлетворяют и этому условию.

Каждому оригиналу (комплексному или действительному) поставим в соответствие функцию 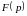комплексного переменного , определенную как интеграл

.

Правая часть этого равенства называется интегралом Лапласа для функции . Функцию будем называть изображением Лапласа (или короче – изображением) оригинала .

Тот факт, что функция является изображением оригинала , будем записывать так ≓ или ≒ (верхняя точка всегда ближе к оригиналу ил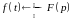и и , где стрелка направлена всегда от изображения к оригиналу).

При этом условимся обозначать оригиналы малыми буквами, а изображения – соответствующими прописными буквами.

Пример 1.

Найти изображение единичной функции Хевисайда, которая обозначается и определяется в соответствии с равенством:

Пользуясь определением изображения, находим , при .

≒

.

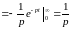Итак: ≒ .

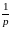Пример 2.

Найти изображение функции .

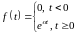И меем = , т.к. .

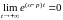Действительно,

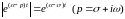
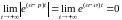при ;

(в дальнейшем предполагается, что этому условию удовлетворяет); а если модуль комплексного переменного стремится к «0», то и само это переменное стремится к «0».

Итак, имеем формулу

.

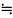
Пользуясь этой формулой, найдем:

; ; ; .

В условии задачи и в формуле предполагается, что 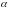- действительное число. Но эту формулу нетрудно обобщить на случай комплексного ; нужно будет только соответствующим образом выбрать .

В дальнейшем будем считать, что все рассматриваемые нами функции снабжены множителем , хотя сам этот множитель будем опускать.

Так, например, мы можем писать и т.д., подразумевая при этом соответственно и т.д.

2. Составление таблицы оригиналов и изображений

На лекции были получены формулы:

; ; ; .

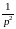Продолжим составление таблицы.

Пример 3.

Найти изображение функции

.

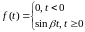По определению

.

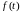
Отыскание изображения здесь довольно громоздкая операция. Найдем изображение иначе:

=

.

, в частности .

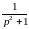Пример 4.

Аналогично найдем изображение функции .

= .

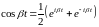
, в частности .

Найти изображения функций , применяя выведенные формулы.

, т.к. 1≒ , то 5≒ .

, т.к. 2≒ , ≒ ,

то ≒ ;

;

;

;

;

.

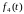
Ответ:

;

;

;

;

.
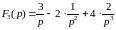
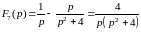