
- •Операционное исчисление
- •1. Преобразование Лапласа и формула обращения
- •1.1. Интеграл Фурье
- •1.2. Преобразование Лапласа и формула обращения
- •2. Основные теоремы и формулы операционного исчисления
- •2.1. Оригинал и изображение
- •Единичная функция
- •Основные свойства изображений
- •2.2. Дифференцирование и интегрирование начальной функции (оригинала) и изображения
- •Дифференцирование оригинала
- •Интегрирование оригинала
- •Дифференцирование изображения
- •Теорема смещения
- •Изображения основных элементарных функций
- •Теоремы разложения
- •Первая теорема разложения
- •5.2. Вторая теорема разложения
- •5.3. Третья теорема разложения
- •Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами методами операционного исчисления
- •Изображение периодической функции
- •Основная литература
- •Дополнительная литература
- •Методические и учебные пособия
5.2. Вторая теорема разложения
Для
того, чтобы найти оригинал функции
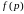 ,
изображение
которой заданно дробно-рациональной
функцией
,
изображение
которой заданно дробно-рациональной
функцией
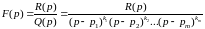 ,
,
(степень числителя меньше степени знаменателя), разлагаем изображение на элементарные дроби, после чего находим оригинал каждой дроби.
Пример
2.
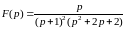
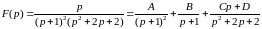 ,
,
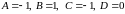 .
.
Получим:
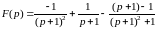 .
.
Запишем оригинал:
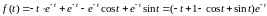 .
.
5.3. Третья теорема разложения
Если
изображением
искомой функции
служит функция комплексного аргумента,
регулярная справа от прямой
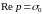 ,
а на этой прямой и слева от нее не имеющая
других особенностей, кроме конечного
множества полюсов и существенно особых
точек, то оригиналом для этой функции
случит функция
,
определяемая по формуле
,
а на этой прямой и слева от нее не имеющая
других особенностей, кроме конечного
множества полюсов и существенно особых
точек, то оригиналом для этой функции
случит функция
,
определяемая по формуле
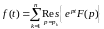 . (5.3)
. (5.3)
Пример
3.
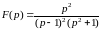
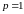 -
полюс 2-го порядка,
-
полюс 2-го порядка,
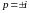 -
полюсы 1-го порядка.
-
полюсы 1-го порядка.
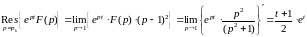 .
.
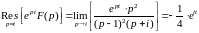 .
.
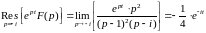 .
.
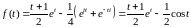 .
.
Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами методами операционного исчисления
Пусть требуется проинтегрировать уравнение
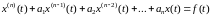 (6.1)
(6.1)
при
начальных условиях: при
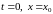
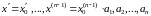 ,
,
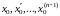 -
заданные постоянные, а
- заданная функция, изображаемая по
Лапласу.
-
заданные постоянные, а
- заданная функция, изображаемая по
Лапласу.
Обозначим
изображение искомого решения через
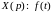
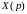 .
.
По теореме дифференцирования оригинала в силу заданных начальных условий имеем:
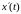
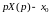
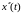
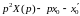 (6.2)
(6.2)
…………………………….
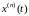
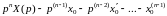 .
.
Пусть, далее, .
Подставляя в (6.1) вместо функций их изображения, получаем так называемой изображающее уравнение:
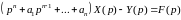 , (6.3)
, (6.3)
которое является алгебраическим относительно изображения искомого решения
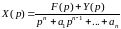 . (6.4)
. (6.4)
Для отыскания решения остается по изображению (6.4) найти его оригинал, пользуясь известными теоремами.
Пример
1.
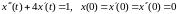
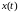
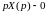
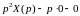
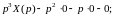 1
.
1
.
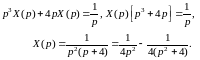
,
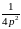
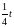 ,
,
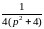
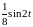 .
.
= - .
Пример 2.
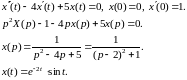
Пример 3. Проинтегрировать уравнение:
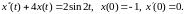
Зная:
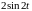
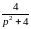 и
,
получим
и
,
получим
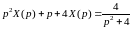 ,
,
отсюда
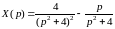 .
.
Оригиналы
для изображений
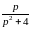 и
известны, а именно:
и
известны, а именно:
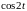 ,
.
,
.
Оригинал
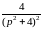 найдем по теореме свертывания:
найдем по теореме свертывания:
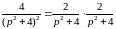
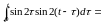
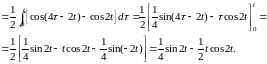
Окончательно:
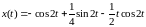
или
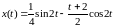 .
.
Изображение периодической функции
Пусть
требуется найти изображение периодической
функции
с
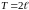 (при
(при
 ).
(При
).
(При
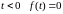 ).
).
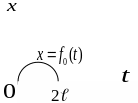
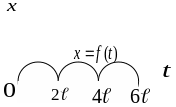
Введем
вспомогательную функцию
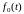 ,
которая на полуотрезке
,
которая на полуотрезке
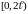 равна
,
вне этого отрезка равна 0, т.е.
равна
,
вне этого отрезка равна 0, т.е.
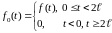 .
.
Ее
изображением будет служить функция
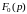 ,
определяемая следующим образом:
,
определяемая следующим образом:
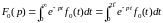 ,
,
т.к. .
Но
функцию
в свою очередь можно выразить через
следующим образом:
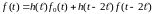 ,
здесь
,
здесь
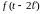 - та же периодическая функция, но с
запаздыванием на один период, равная
нулю при
- та же периодическая функция, но с
запаздыванием на один период, равная
нулю при
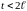 .
Переходя в последнем равенстве к
изображениям и используя теорему
запаздывания, получаем:
.
Переходя в последнем равенстве к
изображениям и используя теорему
запаздывания, получаем:
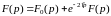 .
.
Отсюда находим
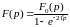 .
.
Таким образом, изображение периодической функции с определяется следующими формулами:
,
где
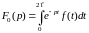 .
.
Пример.
В качестве примера найдем изображение
функции
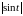 .
.
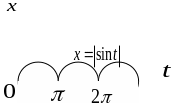
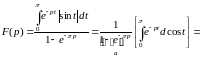
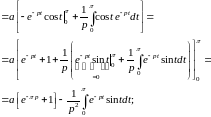
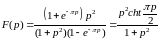 .
.
Л И Т Е Р А Т У Р А
Основная литература
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1966.-331с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Учебник для вузов (под ред. В.С.Зарубина и А.П. Крищенко). – М.: МГТУ, –1996. (Серия «Математика в техническом университете», вып. XI).
Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задача и упражнения. – М.: Наука, 1981. – 215с.
Сборник задач по математике для втузов. Специальные разделы математического анализа. Под ред.Ефимова А.В., Демидовича Б.П., т.2. – 2-е изд. - М.: Наука, 1986.-368с.
