
- •Операционное исчисление
- •1. Преобразование Лапласа и формула обращения
- •1.1. Интеграл Фурье
- •1.2. Преобразование Лапласа и формула обращения
- •2. Основные теоремы и формулы операционного исчисления
- •2.1. Оригинал и изображение
- •Единичная функция
- •Основные свойства изображений
- •2.2. Дифференцирование и интегрирование начальной функции (оригинала) и изображения
- •Дифференцирование оригинала
- •Интегрирование оригинала
- •Дифференцирование изображения
- •Теорема смещения
- •Изображения основных элементарных функций
- •Теоремы разложения
- •Первая теорема разложения
- •5.2. Вторая теорема разложения
- •5.3. Третья теорема разложения
- •Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами методами операционного исчисления
- •Изображение периодической функции
- •Основная литература
- •Дополнительная литература
- •Методические и учебные пособия
2.2. Дифференцирование и интегрирование начальной функции (оригинала) и изображения
В дальнейшем при формулировке и доказательстве теорем операционного исчисления мы всегда будем считать, что все рассматриваемые начальные функции:
изображаемы по Лапласу;
нужное число раз дифференцируемы;
имеют производные, также изображаемы по Лапласу.
Оригинал будем обозначать малыми буквами, а изображения – соответствующими большими буквами (например, ,
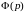 и
т.д.).
и
т.д.).
Дифференцирование оригинала
Допустим,
что оригинал
дифференцируемая функция и его производная
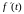 также является оригиналом, причем
также является оригиналом, причем
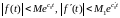 при
.
при
.
Пусть
,
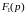 .
Найдем связь между
и
.
По определению изображения имеем
.
Найдем связь между
и
.
По определению изображения имеем
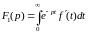 .
.
Выберем здесь так, чтобы одновременно выполнялись неравенства
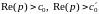 .
Выполняя
в правой части интегрирование по частям,
причем
.
Выполняя
в правой части интегрирование по частям,
причем
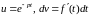 ,
находим
,
находим
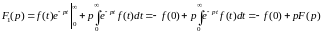 .
.
Таким образом, мы получили следующий результат: из соотношения следует соотношение
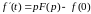 . (2.2)
. (2.2)
Предполагая,
что оригинал
дифференцируем
 раз и что
раз и что
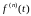 также является оригиналом, методом
индукции из формулы (2.2) получим следующий
результат:
также является оригиналом, методом
индукции из формулы (2.2) получим следующий
результат:
Из соотношения следует соотношение
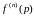
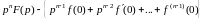 . (2.3)
. (2.3)
Например,
зная, что
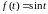
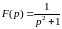 ,
имеем
,
имеем
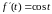
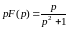 ;
;
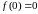 .
.
Интегрирование оригинала
Примем
без доказательства, что если
- оригинал, то оригиналом будет служить
и
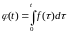 .
.
Найдем теперь изображение .
Так
как
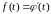 ,
то полагая
,
по формуле (2.2) находим связь между
и
:
,
то полагая
,
по формуле (2.2) находим связь между
и
:
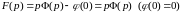 ,
,
отсюда
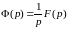 .
Мы пришли к следующему результату:
.
Мы пришли к следующему результату:
Из соотношения следует
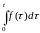
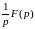 . (2.4)
. (2.4)
Например:
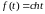
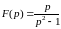 ,
,
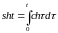
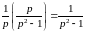 ,
,
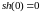 .
.
Т.е.
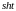
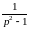 .
.
Дифференцирование изображения
В теории функций комплексного переменного доказывается, что несобственный интеграл
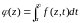 ,
,
в
котором
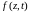 - есть регулярная функция комплексного
переменного
- есть регулярная функция комплексного
переменного
 в замкнутой области
в замкнутой области
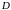 и
непрерывная функция вещественного
переменного
при всяком
и
непрерывная функция вещественного
переменного
при всяком
 ,
можно дифференцировать под знаком
интеграла:
,
можно дифференцировать под знаком
интеграла:
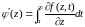 ,
если интеграл этот сходится равномерно
относительно
,
причем теорема остается верной и для
несобственного интеграла, в котором
подинтегральная функция
становится неограниченной.
,
если интеграл этот сходится равномерно
относительно
,
причем теорема остается верной и для
несобственного интеграла, в котором
подинтегральная функция
становится неограниченной.
Говоря
о свойствах изображения, было установлено,
что изображение является регулярной
функцией комплексного переменного
в полуплоскости
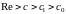 и что в этой полуплоскости дифференцирование
изображения можно выполнять под знаком
интеграла Лапласа. Поэтому из равенства
и что в этой полуплоскости дифференцирование
изображения можно выполнять под знаком
интеграла Лапласа. Поэтому из равенства
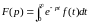 следует
следует
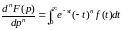 .
.
Но
в правой части стоит изображение функции
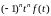 ,
которая является оригиналом, если
оригиналом будет
.
Таким
образом, из соотношения
следует
,
которая является оригиналом, если
оригиналом будет
.
Таким
образом, из соотношения
следует
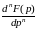 . (2.5)
. (2.5)
Например,
1 ,
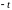
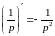 ,
,
т.е.
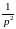 .
.
Интегрирование изображения
Если
функция
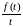 является изображаемой по Лапласу, то
имеет место соотношение:
является изображаемой по Лапласу, то
имеет место соотношение:
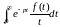 .
.
Заменяя
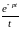 интегралом
интегралом
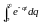 ,
получим:
,
получим:
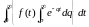
или, если в правой части изменить порядок интегрирования,
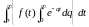
или
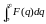 ,
,
где
 .
.
Таким образом, если и функция изображаема по Лапласу, то
. (2.6)
Пример:
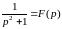 ,
,
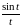
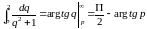 .
.
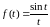
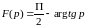 .
.
3. Основные теоремы операционного исчисления
Теорема подобия
Если
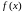 и
и
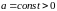 ,
то
,
то
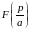 . (3.1.)
. (3.1.)
Доказательство.
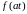
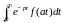 .
.
Пусть
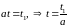 ,
а
,
а
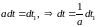 ,
тогда
,
тогда
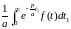 ,
или
,
или
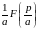 .
.
Из
формулы (3.1) понятно, что увеличению
независимой переменной оригинала в
 раз, соответствует уменьшение в
раз
независимой переменной изображения и
уменьшение в
раз
самого изображения.
раз, соответствует уменьшение в
раз
независимой переменной изображения и
уменьшение в
раз
самого изображения.
Теорема запаздывания
Вспомним понятие единичной функции.
Единичной функцией называется функция, определяемая следующим образом:
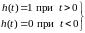 .
.
Функцию,
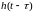 где
где
 - положительная постоянная, называют
единичной функцией запаздывающего
аргумента и означают:
- положительная постоянная, называют
единичной функцией запаздывающего
аргумента и означают:
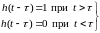 (3.2)
(3.2)
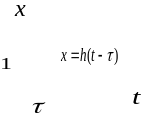
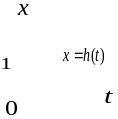
Рис. 3.1. Рис. 3.2.
Очевидно,
что если под
подразумевать время, то функция
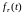 определит течение того же процесса, что
и функция
,
но происходящего с запаздыванием на
время
.
определит течение того же процесса, что
и функция
,
но происходящего с запаздыванием на
время
.
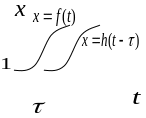
Рис. 3.3.
Функция
может быть представлена в виде произведения
запаздывающей единичной функции
на данную функцию
при замене в последней
через
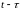 :
:
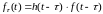 .
.
Зная
изображение
функции
,
можно найти изображение
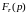 функции
,
пользуясь формулой
функции
,
пользуясь формулой
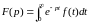 .
.
Имеем
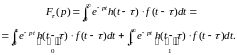
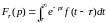 .
.
Применяя
подстановку
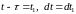 ,
при которой, если
,
при которой, если
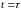 ,
то
,
то
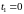 ;
если
;
если
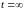 ,
то
,
то
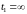 ,
имеем
,
имеем
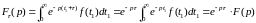 .
.
Таким образом:
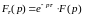
то есть
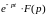

Или, зная , найдем
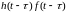
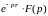 (3.3)
(3.3)
