Операционное исчисление

1. Преобразование Лапласа и формула обращения

1.1. Интеграл Фурье

Пусть в промежутке 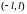функция 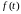удовлетворяет условиям Дирихле, а именно:

а) ограничена на этом отрезке;

б) кусочно-непрерывна на нем (имеет конечное число точек разрыва первого рода);

в) кусочно-монотонная (в частности, имеет лишь конечное число экстремумов).

Тогда, как известно из теории тригонометрических рядов, функция может быть на этом отрезке представлена сходящимся к ней тригонометрическим рядом

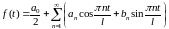. (1.1)

По теореме Дирихле:

1. в точках непрерывности сумма ряда равна значению функции;

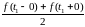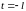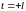2. в точках разрыва сумма ряда равна , а на концах промежутка , то есть при и равна .

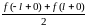Коэффициенты ряда (1.1) определяются по формулам Эйлера-Фурье:

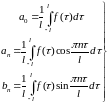(1.2)

Так как косинус есть функция четная, а синус – функция нечетная, то 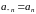, , 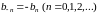формулу (1.1) можно записать в виде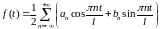 или, с учетом формул (1.2),

,

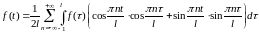откуда

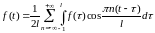. (1.3)

Обозначим

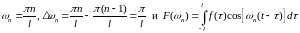, (1.4)

приведем формулу (1.3) к виду:

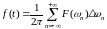. (1.5)

Если в промежутке функция абсолютно интегрируема, т.е.

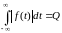, (1.6)

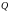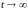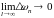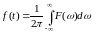где - конечное число, то переходя в равенстве (1.5) к пределу при и замечая, что , получаем формулу: , или

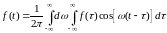. (1.7)

Интеграл, стоящий в правой части равенства (1.7), называется интегралом Фурье.

Замечая, далее, что

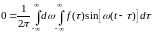(1.8)

(т.к. 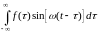- является нечетной функцией аргумента 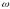) преобразуем формулу (1.7)

,

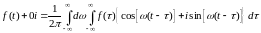откуда

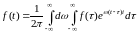. (1.9)

Интеграл, стоящий в правой части формулы (1.9), называется интегралом Фурье в комплексной форме.

1.2. Преобразование Лапласа и формула обращения

Докажем теперь, что если функция не интегрируема абсолютно, удовлетворяет условиям:

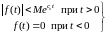, (1.10)

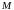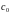Где и - некоторые постоянные положительные числа, то при

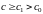(11.10а)

функцию

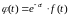(1.10б)

можно представить интегралом Фурье:

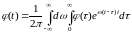. (1.10в)

В самом деле, если условия (1.10) и (1.10а) выполняются, то

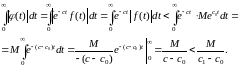
Таким образом, в интервале функция 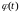оказывается абсолютно интегрируемой, что и доказывает возможность представления ее в этом интервале интегралом Фурье (1.10в).

Заменяя в равенстве (1.10в) на 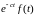(формула (1.10б)):

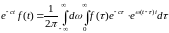
и умножая обе части этого равенства на 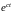, получим

,

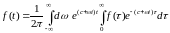обозначим

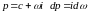. (1.11)

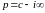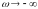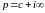Так как при ; при 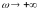, то последняя формула для принимает вид:

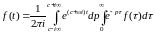, (1.12)

это преобразованный интеграл Фурье.

Если положить:

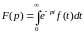, (1.13)

То

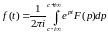. (1.14)

В операционном исчислении формула (1.13) является основной. Формула эта, в правой части которой стоит так называемый интеграл Лапласа, определяет преобразование Лапласа, при помощи которого функция вещественного независимого переменного 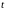преобразуется в функцию 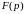комплексного независимого переменного .

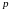Функцию называют начальной функцией или оригиналом, а функцию , получаемую из при помощи преобразования Лапласа, изображением функции .

Легко доказать, что, если функция удовлетворяет условиям Дирихле и условиям (1.10), то изображение представляет собой функцию, регулярную при всех значениях комплексного независимого переменного 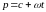, удовлетворяющих неравенствам (1.10а), то есть регулярную по всей полуплоскости, расположенной справа от прямой .

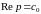Формула (1.14), в правой части которой стоит так называемый интеграл обращения, определяет преобразование обратное преобразованию Лапласа, то есть преобразование, при помощи которого функция комплексного переменного преобразуется в функцию вещественного независимого переменного .