Решение.

Приведем таблицу, определяющую потери в тысячах долларов.

Принцип Лапласа предполагает, что q 1, q 2, q 3, q 4 равновероятны.

Следовательно, P{q =q j } =1/4, j= 1, 2, 3, 4, и ожидаемые потери при различных действиях a1, a2, a3, a4 составляют

E{a1}= (1/4)(5+10+18+25)=14,5

E{a2}= (1/4)(8+7+8+23)=11,5

E{a3}= (1/4)(21+18+12+21)=18,0

E{a4}= (1/4)(30+22+19+15)=21,5

Таким образом, наилучшим уровнем предложения в соответствии с критерием Лапласа будет a2.

5. Одно из предприятий должно определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течение предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принять одно из четырех значений: 200, 250, 300 или 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса (решить задачу используя принцип минимакса).

Решение.

Приведем таблицу, определяющую потери в тысячах долларов.

Решение.

Основывается на выборе наилучшей из наихудших возможностей. Если результат n (ai , q j) представляет потери лица, принимающего решение, для действия ai наибольшие потери независимо от возможного состояния q j будут равны

6. Фирма планирует реализацию одного из коммерческих проектов. Причем известны экспертные оценки, связанные с реализацией этих проектов (таблица 1.1).

Выбрать рациональный вариант коммерческого проекта, если среднегодовая прибыль от реализации проекта должна быть не менее 4,5 млн. у.е. при минимальном риске.

Задачу решить по следующей схеме:

-оценить эффективность проекта по критерию ожидаемой среднегодовой прибыли;

-определить допустимые проекты, исходя из заданного уровня среднегодовой прибыли;

-оценить риск допустимых проектов на основе коэффициента вариации ожидаемой среднегодовой прибыли;

-из множества допустимых проектов выбрать рациональный вариант коммерческого проекта, которому соответствует минимальный риск.

Таблица 1.1

Исходные данные для расчета

Оценка ожидаемой прибыли	Проект
	1	2	3	4	5	6
Пессимистическая оценка Xmin (млн. у.е. в год)	4	4	3	4	2	2
Оптимистическая оценка Xmax (млн. у.е. в год)	8	7	6	9	10	8

Решение

Степень риска коммерческого проекта возможно оценить с помощью коэффициента вариации, который характеризует относительный разброс случайной величины в виде ожидаемой прибыли от реализации проекта.

. (1.1)

Чем больше коэффициент вариации, тем больше неопределенность в отношении ожидаемой прибыли и, следовательно, тем больше степень риска коммерческого проекта. Причем принято выделять следующие уровни риска:

Kvar < 10% - малая степень риска;

Kvar = (10-25)% - средняя степень риска;

Kvar > 25% - высокая степень риска.

MO и SIGMA ожидаемой среднегодовой прибыли от реализации коммерческих проектов определяется на основе приближенных соотношений для 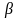-распределения:

;

.

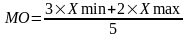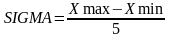Таблица 1.2

Оценка степени риска коммерческого проекта

Показатель	Проект
	1	2	3	4	5	6
МО	5,6	5,2	4,2	6,0	5,2	4,4
SIGMA	0,8	0,6	0,6	1,0	1,6	1,2
Kvar	14,3	11,5	14,3	16,7	30,8	27,3
Степень риска	средняя	средняя	средняя	средняя	высокая	высокая

По критерию ожидаемой среднегодовой прибыли (МО) предпочтителен проект № 4 (самая большая прибыль);

По уровню среднегодовой прибыли (SIGMA) наиболее благоприятен проект №4 (уровень равен 1,0).

На основе коэффициента вариации выберем проект № 2 (самая малая степень риска).

Из множества допустимых проектов выбрать самым рациональным является проект №4.