Задачи по имитационному моделированию

1. Ежедневный спрос на некоторый товар (β) составляет 100ед. Затраты на размещение каждого запаса (К) постоянны и равны 100долл. Ежедневные затраты на хранение единицы запаса (h) составляют 0,02долл. Определить экономичный размер партии и точку заказа при сроке выполнения заказа, равном 12 дням.

Решение.

Из формулы Уилсона получаем:

=1000 ед.

Тогда оптимальная продолжительность цикла составляет:

Т.к. срок выполнения заказа равен 12 дням и продолжительность цикла составляет 10 дней, возобновление заказа происходит, когда уровень запаса достаточен для удовлетворения спроса на 12-10=2 дня. Таким образом, заказ размером у*=1000 размещается, когда уровень запаса достигает 2*100=200ед.

Можно считать, что эффективный срок выполнения заказа равен где L - заданный срок выполнения заказа.

Варианты задачи:

а) срок выполнения заказа L=15 дней. (Ответ. 500ед.)

б) L=23 дня. (Ответ. 300ед.)

в) L=8 дней. (Ответ. 800ед.)

г) L=10 дней. (Ответ. 0 ед.)

2. Необходимость в проведении профилактического ремонта оборудования требует принятия решений о том, когда следует проводить плановый ремонт какого-нибудь станка (или другого вида оборудования), чтобы минимизировать потери из-за неисправности (отказа). Если весь временной горизонт разбит на равные периоды, то решение заключается в определении оптимального числа периодов между двумя последующими ремонтами. В случае, когда они производятся слишком часто, затраты на обслуживание будут большими при малых потерях из-за случайных отказов. Компромисс между двумя случаями предусматривает сбалансированный выбор между затратами на ремонт и потерями из-за случайных отказов.

Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо вычислить вероятность того, что станок выйдет из строя в период времени t. В данном случае это и есть элемент риска в процессе принятия решения.

Станок из группы в n станков ремонтируется индивидуально, если он остановился из-за неисправности. Через Т интервалов времени выполняется профилактический ремонт всех n станков. Задача состоит в определении оптимального значения Т, при котором минимизируются общие затраты на ремонт вышедших из строя станков и проведение профилактического ремонта в расчете на один интервал времени.

Пусть pt - вероятность выхода из строя одного станка в момент t, а nt - случайная величина, представляющая число вышедших из строя станков в тот же момент. Далее предположим, что c1 - затраты на ремонт вышедшего из строя станка и c2 - затраты на профилактический ремонт одного станка.

Применение критерия ожидаемого значения в данном случае оправданно, если станки работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят:

МC(t)= , где - математическое ожидание числа вышедших из строя станков в момент t. Так как nt имеет биномиальное распределение с параметрами (n,pt), то = npt. Таким образом,

Необходимые условия оптимальности для Т* имеют вид

MC(T*-1)>= MC(T*) и MC(T*+1)>= MC(T*).

Следовательно, начиная с малого значения Т, вычисляем МС(Т), пока не будут удовлетворены эти условия.

Положим c1= 100 долл, c2=10 долл и n=50. Значения pt приведены в виде таблицы.

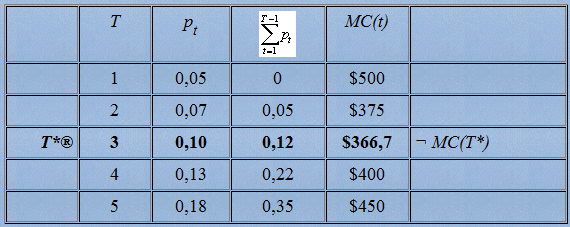
Из этой таблицы видно, что профилактический ремонт необходимо проводить через каждые три (T*=3) интервала времени.

Предположим, что в примере чистая продукция в расчете на один станок в единицу времени составляет а долл и требуется максимизировать доход, приходящийся на единицу времени. Положим также, что доход подсчитывается как разность между общей величиной чистой продукции и затратами на ремонт вышедших из строя станка и обслуживание. Общее выражение для МC(t):

МC(Т)= .

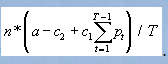Необходимое условие на Т*, максимизирующего МC(Т):

MC(T*)>= MC(T*-1) и MC(T*)>= MC(T*+1).

3. Когда следует проводить плановый ремонт какого-нибудь станка (или другого вида оборудования), чтобы минимизировать потери из-за неисправности (отказа).

Для этого необходимо вычислить дисперсию затрат за один интервал:

Используя данные из предыдущей лекции, составим таблицу:

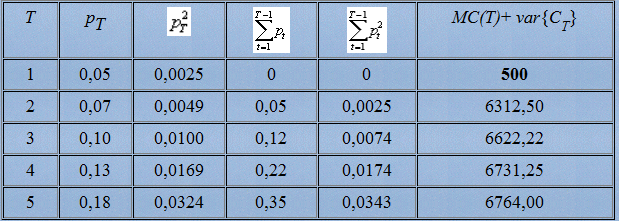
Из таблицы видно, что профилактический ремонт следует проводить в течение каждого интервала времени (Т*=1).

4. Одно из предприятий должно определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течение предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принять одно из четырех значений: 200, 250, 300 или 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса (решить задачу используя принцип Лапласа).