31

Практикум по финансовой математике

(автор Галиаскаров Ф.М.)

2011 г.

Глава 1. Основные формулы, применяемые в финансовых расчетах

1.1. Простые и сложные проценты

Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени.

Проценты различаются по базе их начисления. Применяется постоянная или последовательно изменяющаяся база для расчета. В последнем случае за базу применяется сумма, полученная на предыдущем этапе наращения или дисконтирования, т.е. проценты начисляются на проценты. При постоянной базе используют простые, при измененной -сложные процентные ставки.

Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока.

Наращение по простой процентной ставке:

, (1)

где S – наращенная сумма; P – первоначальная сумма, n – срок, r – ставка наращения (десятичная дробь).

Наращение по сложной процентной ставке:

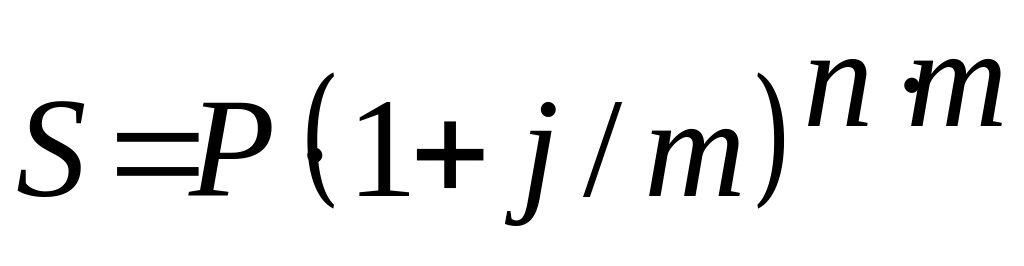, (2)

где j - сложная процентная ставка; n - число лет наращения, m – число начислений процентов в году.

Номинальная ставка – это годовая ставка сложных процентов при одноразовом начислении процентов в году по ставке j.

Эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов в году по ставке .

Наращение по непрерывной процентной ставке:

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста ( ). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.

, (3)

Дисконтирование и учет по простым процентным ставкам.

Термин дисконтирование употребляется как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n , необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты - дисконтом

В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.

Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.

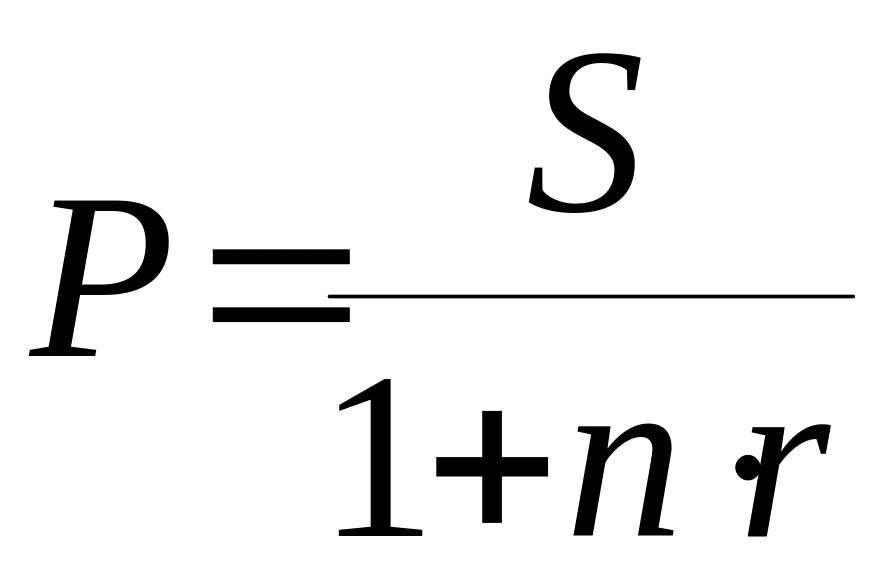, (4)

Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.

, (5)

Для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении .

Ставка Прямая задача Обратная задача

r (6)

d .

Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.

Определение срока ссуды и величины простой процентной ставки

Продолжительность срока ссуды в годах получим, решив уравнения (1) и (5) относительно n:

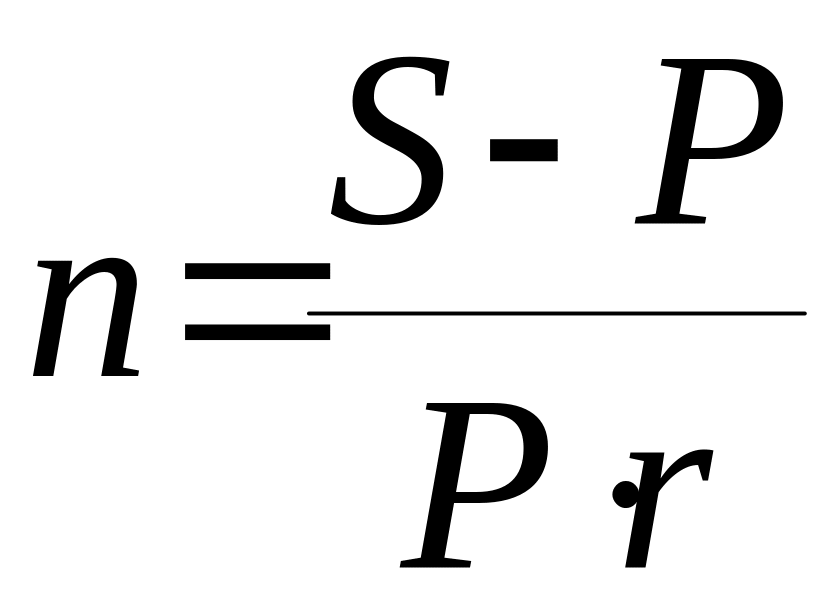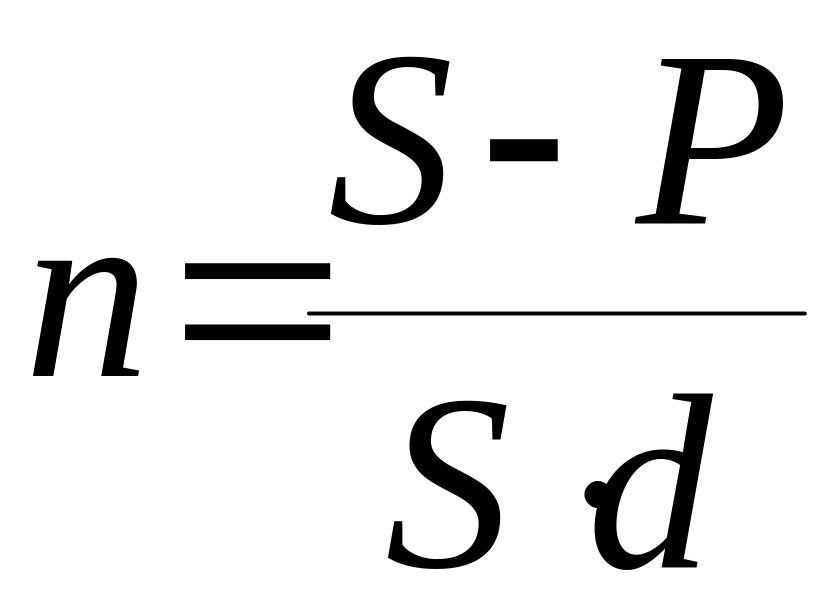, (7) , (8)

По этим же уравнениям можно определить и процентные ставки:

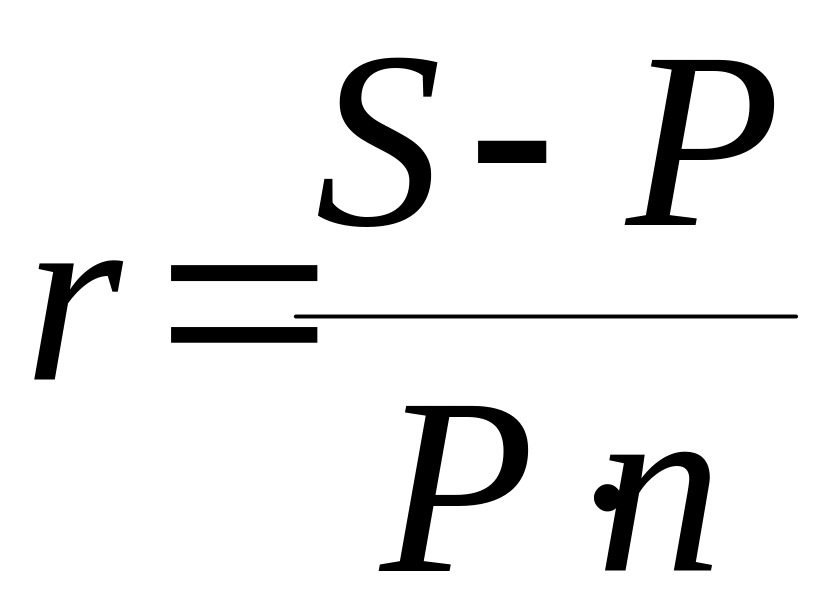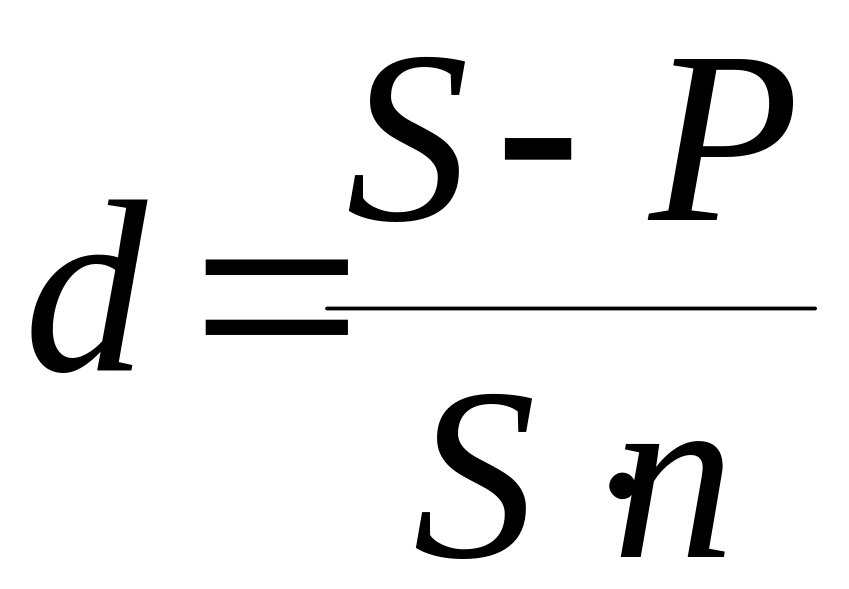, (9) , (10)

Определение срока платежа и сложных процентных ставок.

Продолжительность срока платежа в годах получим, решив уравнения (2) относительно n:

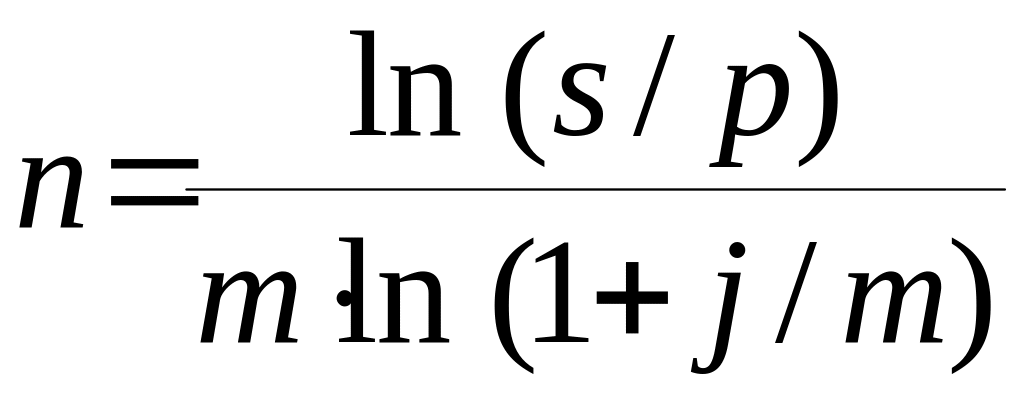, (11)

Поэтому же уравнению можно определить и сложную процентную ставку:

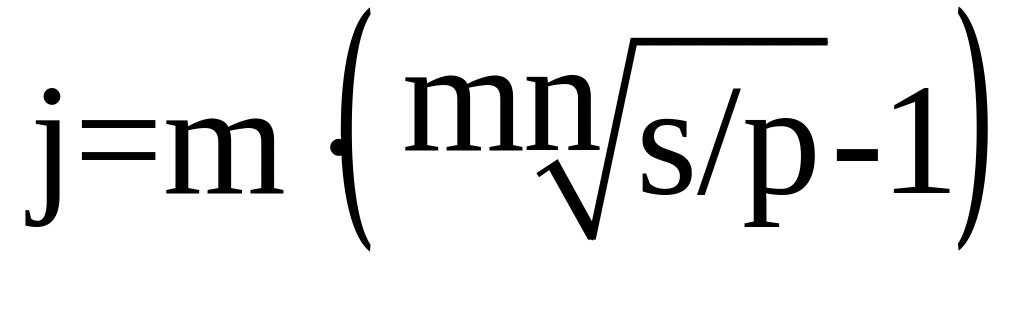, (12)

Продолжительность срока платежа в годах при наращении по постоянной силе роста и по изменяющейся с постоянным темпом силе роста получим, решив уравнения (3) относительно n:

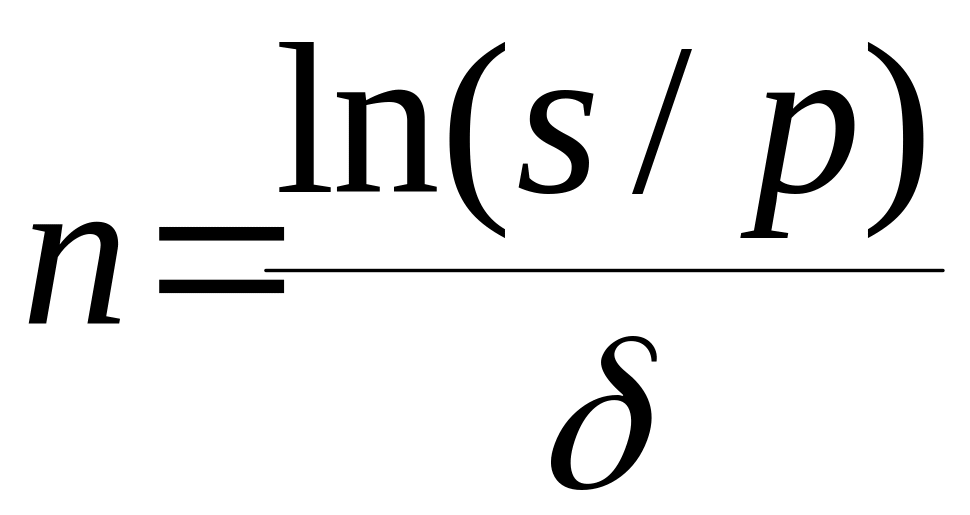, (13)

Поэтому же уравнению можно определить и силе роста :

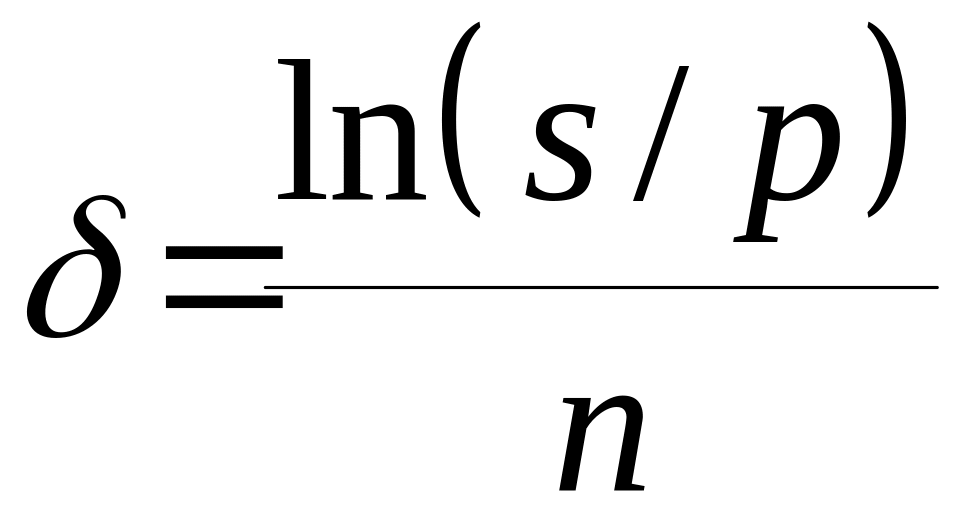, (14)