53. Сущность и техника выполнения кинематической проверки результатов расчёта методом перемещений.

(32, 76) В каком случае кинематическая проверка не нужна? (33) Кинематическая ( деформационная ) проверка – вычисление перемещений, которые в заданной системе заведомо равны нулю ( по направлениям жёстких связей ).

Кинематическая ( деформационная ) проверка – выполняется с использованием статически определимой основной системы метода сил, в которой определяются суммарные единичные усилия от Х₁ = 1, Х₂ = 1, …, Х_n = 1 ( рис. 2.29 ).

Х₁ = 1

Х₂ = 1

Х₃ = 1

Х₄ = 1

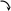
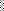
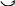
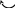
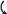
1

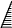
1

1

Рис. 2.29

Обобщённое перемещение по направлениям лишних связей, которое при отсутствии ошибок в результатах расчёта должно быть равным нулю, находим по формуле, получающейся из ( 1.30 ) как частный случай для рассматриваемой рамы с одной упругой опорной связью:

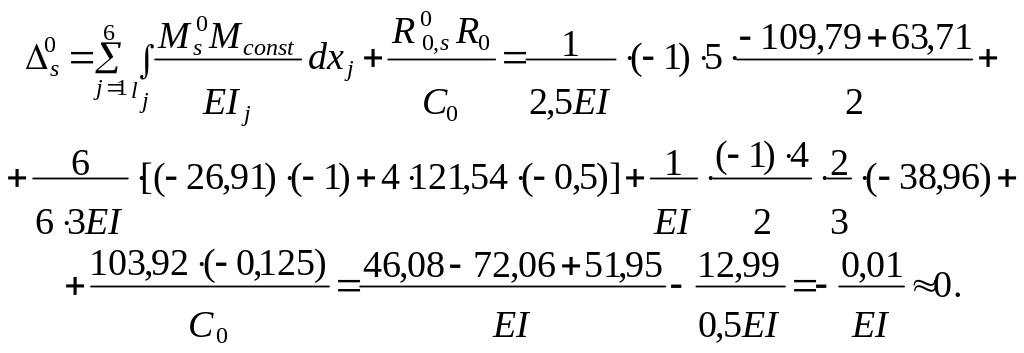
В случае расчёта методом перемещений статически определимой деформируемой системы кинематическая проверка результатов не выполняется, так как в системах без лишних связей условия совместности перемещений и кинематические граничные условия удовлетворяются автоматически.

54. Формулы кинематической проверки (универсальной и раздельной, в обычной и матричной формах) при силовых, температурных и кинематических воздействиях. (32, 40)

Для выполнения этой проверки используются усилия в выбранной вспомогательной ОСМС от единичного основного неизвестного метода сил X_i = 1. Перемещение по направлению i - й удалённой лишней связи, которое должно быть равным нулю, определяется как

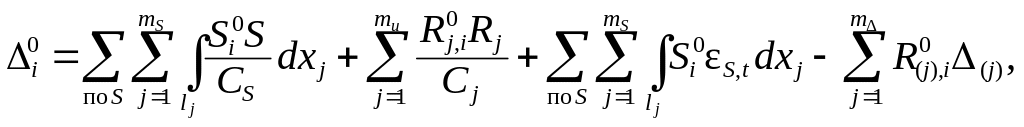( 1.28 )

где , , – соответственно внутренние усилия, реакции

упругих и смещаемых связей в ОСМС от X_i = 1;

S и R_j – найденные расчётом по методу перемещений

внутренние усилия и реакции упругих связей.

Наряду с частными ( раздельными ) проверками = 0 (?) ( i = ) может выполняться универсальная кинематическая проверка = 0 (?). Обобщённое перемещение по направлениям всех удалённых лишних связей

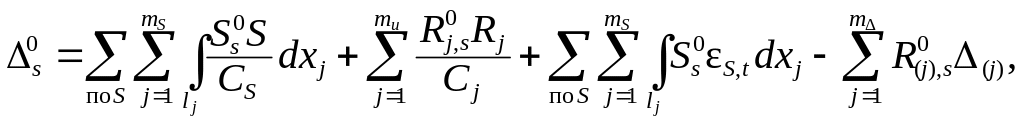( 1.29 )

где , , – суммарные единичные силовые факторы в ОСМС от одновременно приложенных всех основных неизвестных X₁ = 1, X₂ = 1, …, = 1.

В общем случае деформации плоской системы при комбинированных воздействиях

( 1.30 )

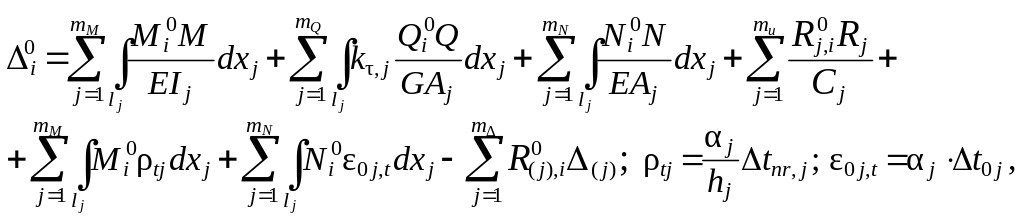
55. Особенности расчёта деформируемых систем методом перемещений (см. [ 5 ]):

а) обусловленные характером воздействия (силовое, температурное, кинематическое);

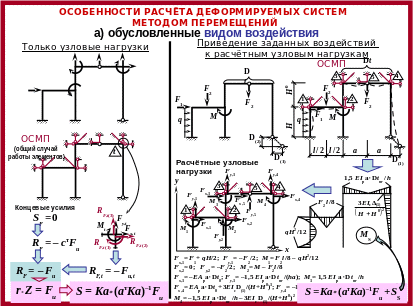
б) для систем разных типов (балки, арки, рамы, фермы, комбинированные системы).

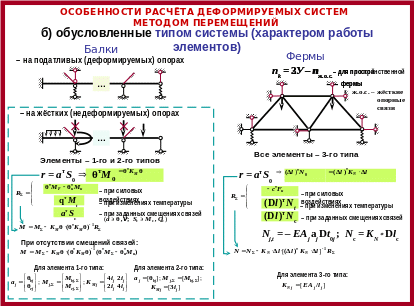
56. Замена заданных внеузловых воздействий расчётными узловыми нагрузками – процедура их определения и особенности расчёта, обусловленные их использованием. (40, 76)

Приведение заданных воздействий

к расчётным узловым нагрузкам

Если нагрузка состоит из сосредоточенных сил и моментов, приложенных только к расчётным узлам ( т.е. отсутствуют внеузловые нагрузки, действующие непосредственно на элементы системы ), то в основной системе МП она не вызывает усилий в концевых сечениях стержней. Строго говоря, если расчёт выполняется с применением гипотезы , то от узловой нагрузки в стержнях возникают продольные силы, но они постоянны по длине, следовательно, N_bj = N_ej , и поэтому решение может строиться с матрицами частного вида ( см. табл. 1.3 ) – без учёта сил N и продольных перемещений концевых сечений. Вследствие этого S_F = 0, и формула для концевых усилий в заданной системе упрощается:

. ( 1.50 )

При наличии внеузловых нагрузок, а также изменений температуры и заданных смещений связей они могут быть заменены эквивалентными сосредоточенными силами и моментами в расчётных узлах так, что в результате такой замены основные неизвестные Z не изменяются. Процедура определения эквивалентных узловых нагрузок такова:

1) с помощью стандартных ( табличных ) данных находятся усилия S_ в элементах ОСМП ( в собственных осях координат ) от внеузловых нагрузок, изменений температуры и заданных кинематических воздействий;

2) к расчётному узлу прикладываются концевые усилия примыкающих к нему элементов ( рис. 1.21, а );

Q_bj,

F_yt,eqvl

у

R_i

j

R_i

а) б)

q

M_bj,

N_bj,

t

t

F_xt,eqvl

M_t,eqvl

t^o

х

0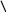

Рис. 1.21

3) переданные в узел t концевые моменты и силы суммируются и определяются их составляющие в общей ( глобальной ) системе координат х0у ( рис. 1.21, б ); они образуют вектор узловых нагрузок, эквивалентных внеузловым воздействиям:

F_t,eqvl = [ M_t,eqvl F_xt,eqvl F_yt,eqvl ]^т ; ( 1.51 )

4) из векторов F_t,eqvl формируется вектор экви-

валентных узловых нагрузок всей системы:

F_{u ,eqvl} = [ … … ]^т ; ( 1.52 )

5) при наличии в узлах заданной системы реальных сосредоточенных нагрузок F_u они суммируются с найденными эквивалентными F_u,eqvl , в результате получается матрица расчётных узловых нагрузок ( 1.53 )

Замечание: определённые вышеизложенным способом

нагрузки оказываются приложенными только к тем узлам, на которые наложены дополнительные связи. Кроме того, если

линейные связи параллельны глобальным осям х и у, то отлич-

ны от нуля только узловые силы и/или по направлениям

соответствующих связей ( так, если в узле t нет связи, параллельной оси у, то расчётная нагрузка = 0 ).

Матрица используется для вычисления концевых усилий по формуле, аналогичной ( 1.50 ):

( 1.54 )

Найденные по ( 1.53 ) усилия находятся в равновесии с рас-чётными узловыми нагрузками, а не с заданными реальными воздействиями. Истинные усилия S получаются добавлением к S^* силовых факторов S_ в ОСМП, упоминавшихся в п. 1 описанной выше процедуры:

S = S^* + S_ . ( 1.55 )

Операция замены заданных воздействий расчётными узловыми нагрузками является стандартной в методе конечных элементов в перемещениях и применима к любым деформируемым системам ( не только стержневым ).