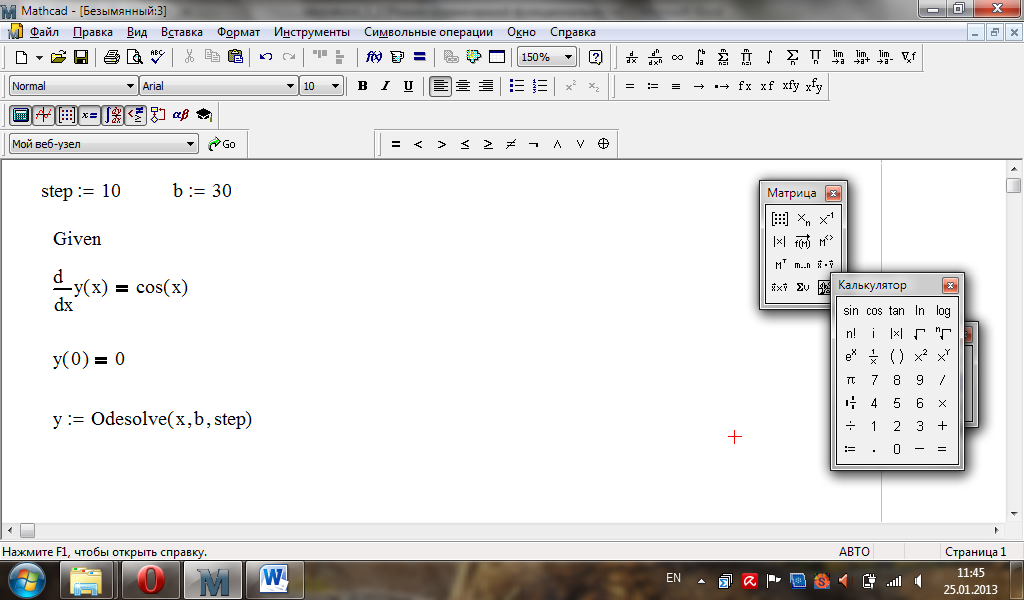
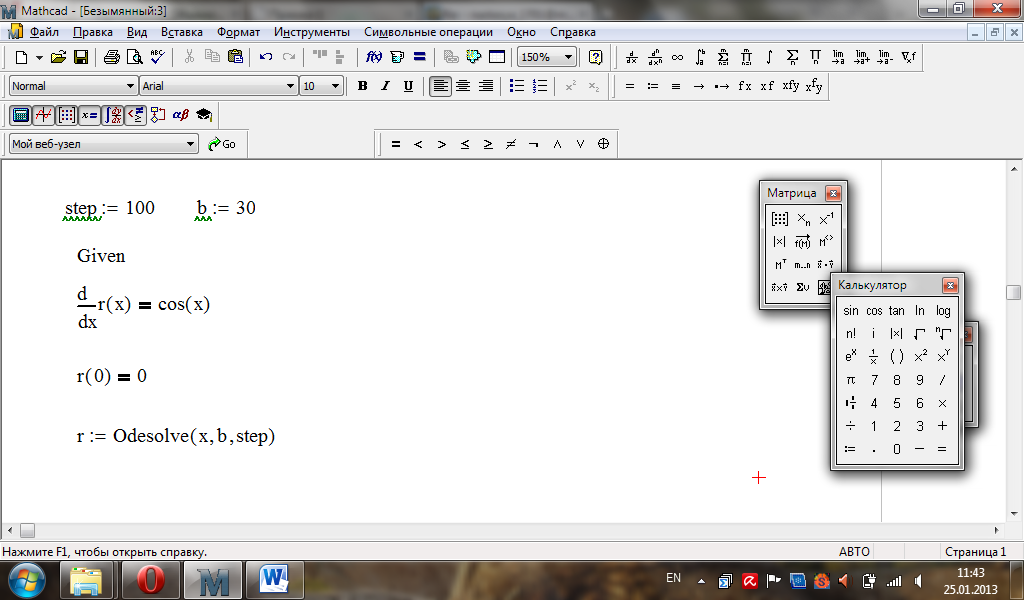
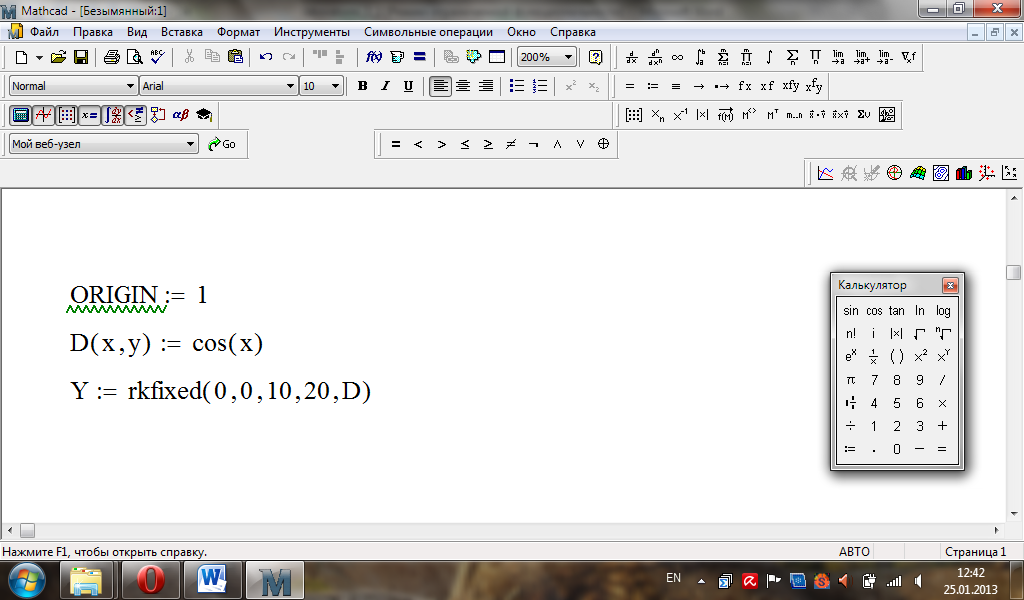
Приклад.

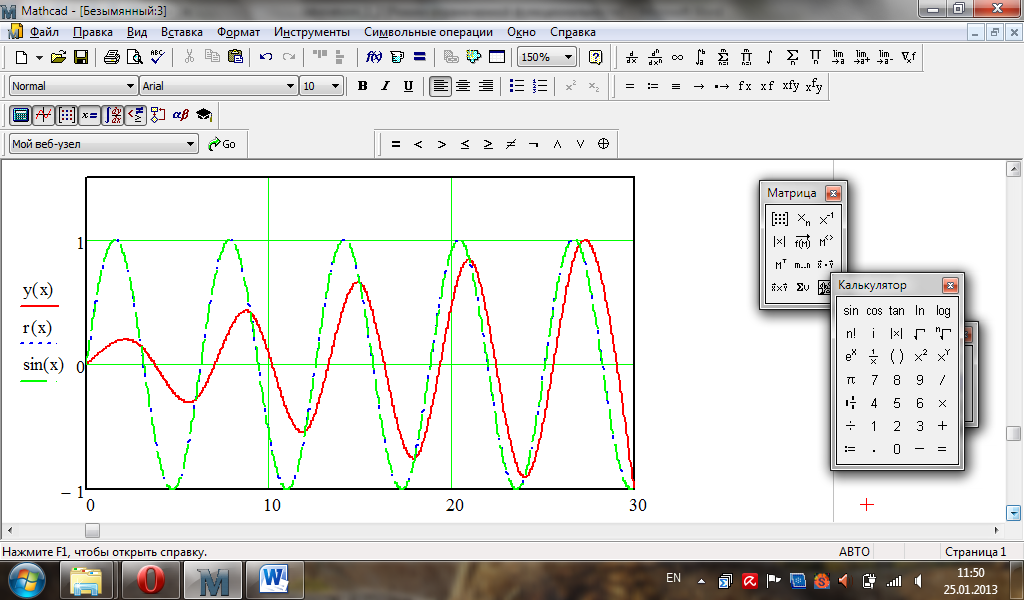
Розв’язати задачу Коші на проміжку за допомогою функцій Odesolve та Rkfixed. Порівняти на графіку знайдений наближений розв’язок з точним (знайденим самостійно). Зміною параметрів step i t, досягти максимального співпадання кривих та .

Обчислення в MathСad:

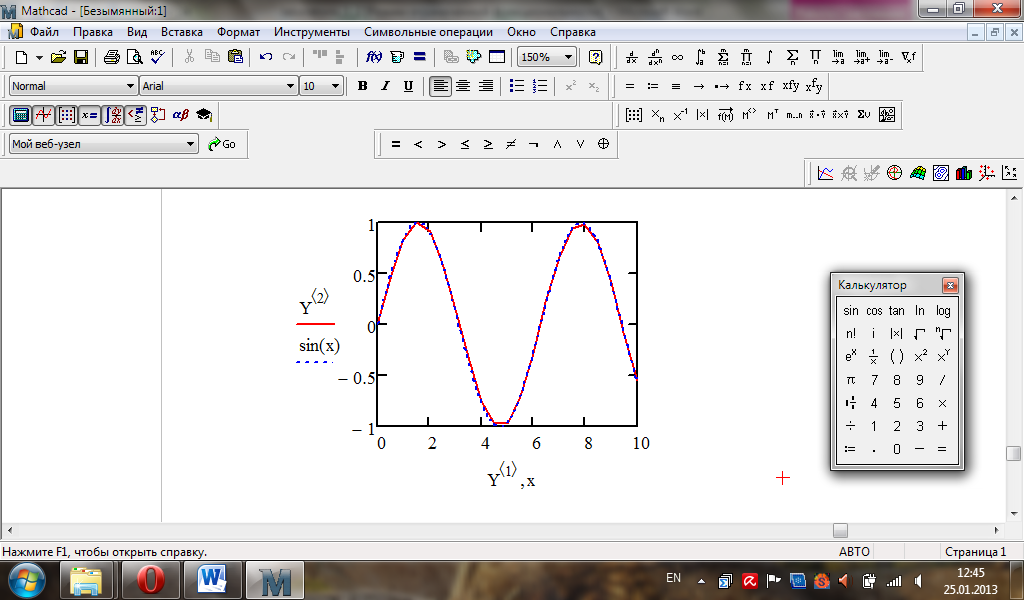
Завдання до лабораторної роботи № 21.

1. Розв’язати задачу Коші на проміжку за допомогою функцій Odesolve та Rkfixed. Порівняти на графіку знайдений наближений розв’язок з точним (знайденим самостійно). Зміною параметрів step i t, досягти максимального співпадання кривих та .

2. Розв’язати рівняння Бернуллі, самостійно вибравши початкову умову та інтервал .

Варіант	Завдання
1	1. 2. , , . 3.
2	1. , , . 2. , , . 3. .
3	1. 2. , , . 3.
4	1. 2. , , . 3.
5	1. 2. , , . 3.
6	1. 2. , , . 3.
7	1. , , . 2. , , . 3. .
8	1. 2. , , . 3. .
9	1. , , . 2. , , . 3. .
10	1. 2. , , . 3.
11	1. , , . 2. , , . 3. .
12	1. , , . 2. , , . 3. .
13	1. , , . 2. , , . 3. .
14	1. . 2. , , . 3.
15	1. , . 2. , , . 3. .
16	1. , , . 2. , , . 3. .
17	1. , . 2. , , . 3. .
18	1. , , . 2. , , . 3. .
19	1. , , . 2. , , . 3. .
20	1. , , . 2. , , . 3. .
21	1. , . 2. , , . 3. .
22	1. , , . 2. , , . 3. .
23	1. , , . 2. , , . 3. .
24	1. , , . 2. , , . 3. .
25	1. , , . 2. , , . 3. .
26	1. , , . 2. , , . 3. .
27	1. , , . 2. , , . 3. .
28	1. , , . 2. , , . 3. .
29	1. , , . 2. , , . 3. .
30	1. , , . 2. , , . 3. .

Лабораторна робота № 22.

Диференціальні рівняння вищих порядків.

Короткі теоретичні відомості.

Для знаходження розв’язків диференціальних рівнянь вищих порядків використовують один з наступних способів: 1) послідовне інтегрування; 2) заміна. Для обчислення інтегралу в програмі Mathcad використовують панель (оператори математичного аналізу). Після набору інтегралу ставимо < > і отримуємо результат.

Приклад.

Розв'язати диференціальне рівняння .

Нехай

Обчислення в MathСad:

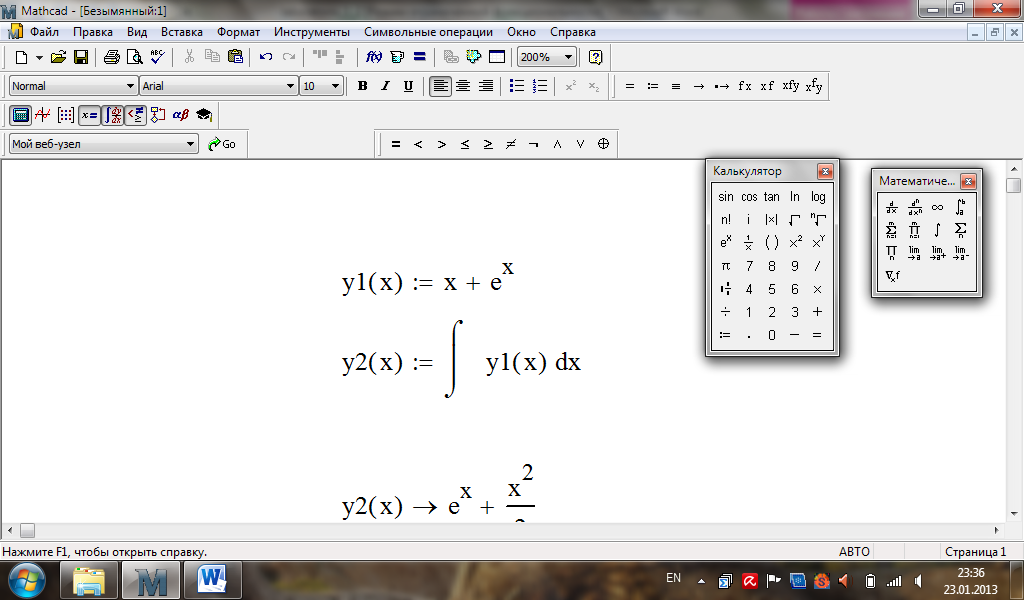
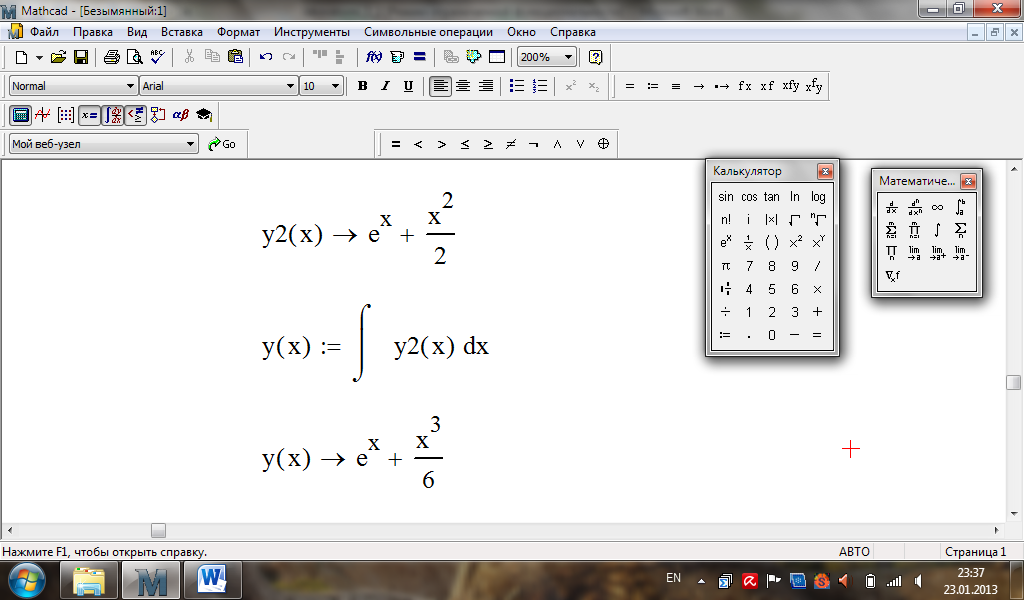
Завдання до лабораторної роботи № 22.

1. Послідовно інтегруючи, розв’язати диференціальні рівняння.

2. Зробивши відповідну заміну, розв’язати диференціальні рівняння.

Варіант	Завдання
1	1. . 2. а) , б) .
2	1. . 2. а) , б) .
3	1. . 2. а) , б)
4	1. . 2. а) , б) .
5	1. . 2. а) , б) .
6	1. . 2. а) , б) .
7	1. . 2. а) , б) .
8	1. . 2. а) , б)
9	1. . 2. а) , б)
10	1. . 2. а) , б) .
11	1. . 2. а) , б) .
12	1. . 2. а) , б)
13	1. . 2. а) , б) .
14	1. . 2. а) , б) .
15	1. . 2. а) , б) .
16	1. . 2. а) , б) .
17	1. . 2. а) , б) .
18	1. . 2. а) , б) .
19	1. . 2. а) , б)
20	1. . 2. а) , б) .
21	1. . 2. а) ,
22	1. . 2. а) , б) .
23	1. . 2. а) , б) .
24	1. . 2. а) , б) .
25	1. . 2. а) , б)
26	1. . 2. а) , б) .
27	1. . 2. а) , б) .
28	1. . 2. а) , б) .
29	1. . 2. а) , б) .
30	1. . 2. а) , б) .

Лабораторна робота № 23.

Лінійні диференціальні рівняння вищих порядків зі сталими коефіцієнтами та із спеціальною правою частиною.

Короткі теоретичні відомості.

Для знаходження розв’язків диференціальних рівнянь вищих порядків зі сталими коефіцієнтами складається та розв’язується характеристичне рівняння. Для розв’язання характеристичного рівняння використовують оператори given(дано) та find(знайти). Те ж виконують при знаходженні сталих (розв’язанні системи).

Приклад

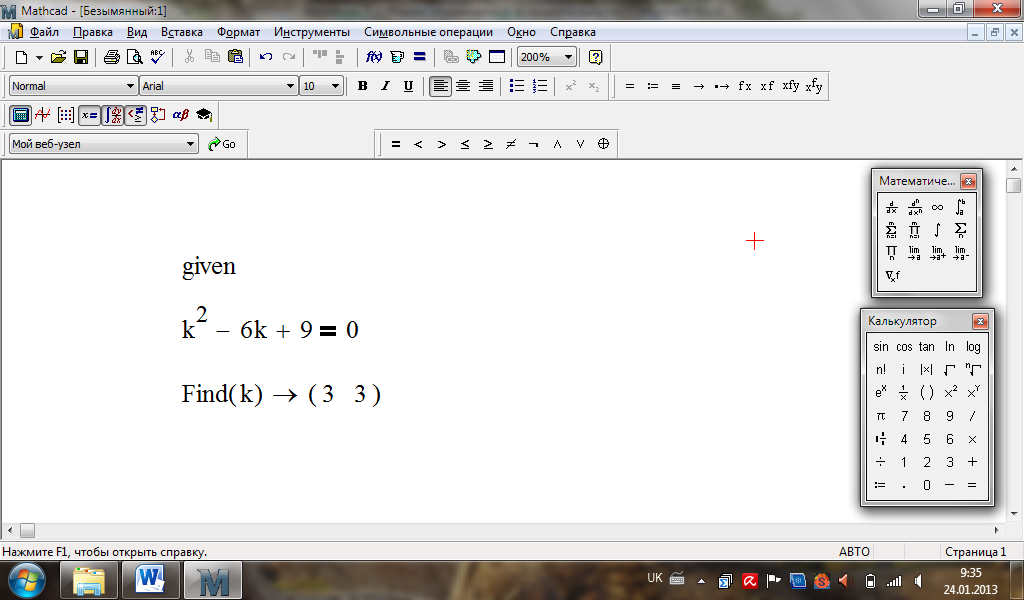
Знайти частинний розв’язок задачі Коші: . Складемо характеристичне рівняння .

Обчислення в MathСad:

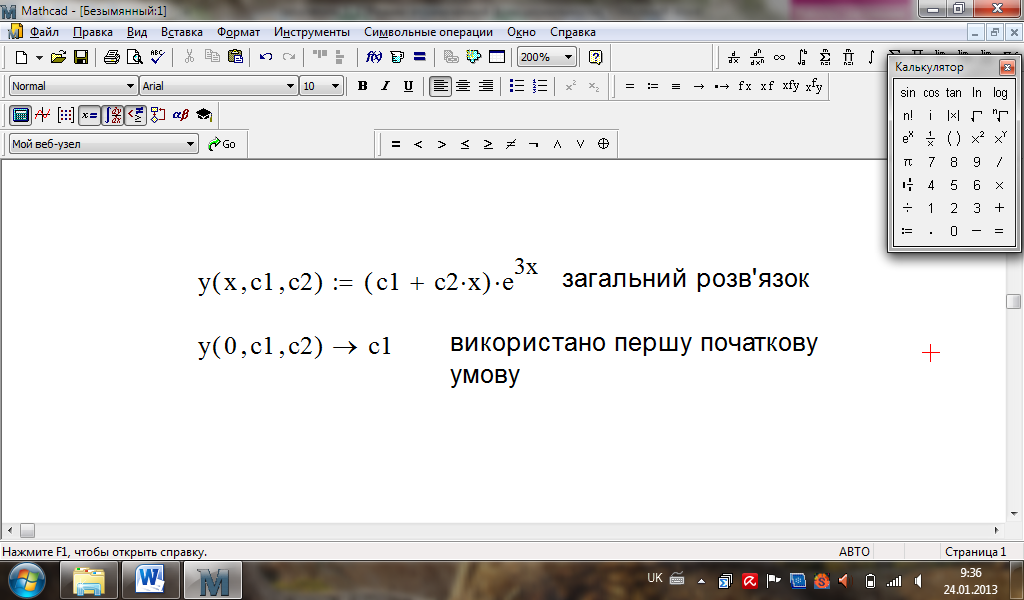
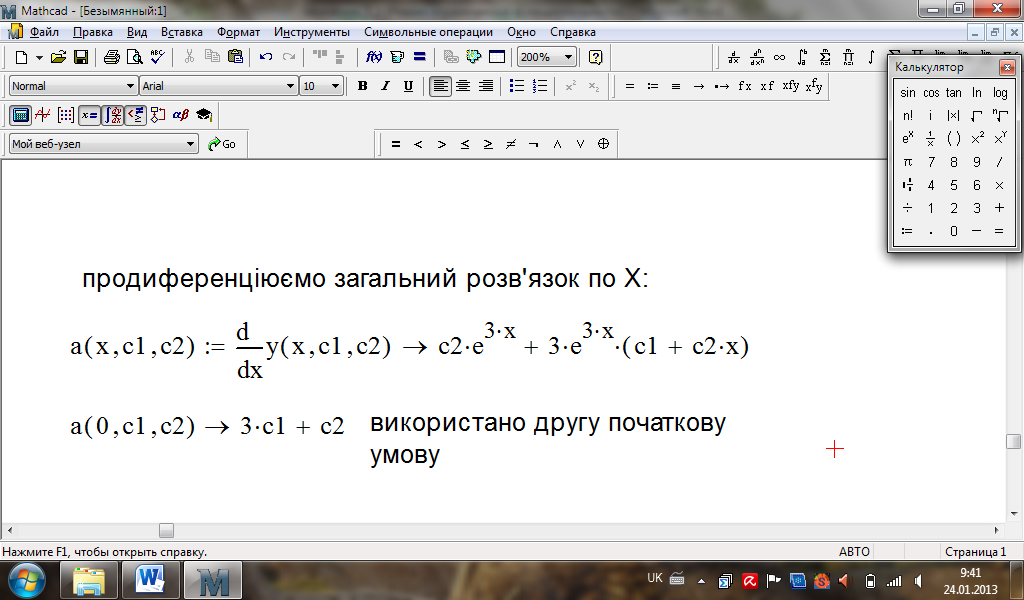
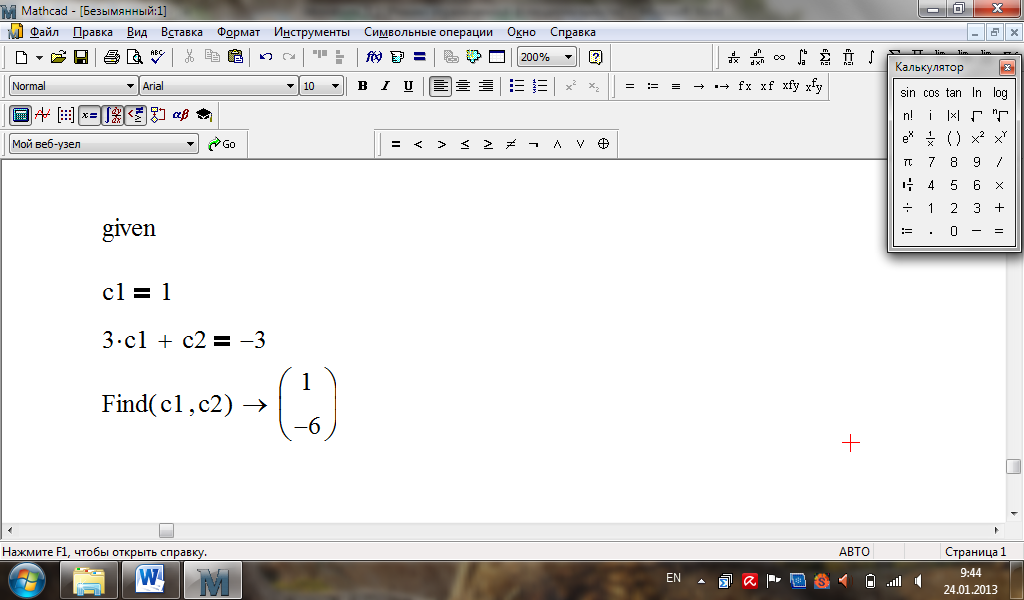
Розв’язок задачі Коші:

Аналогічні міркування при розв’язуванні неоднорідних диференціальних рівнянь другого порядку із спеціальною правою частиною.

Завдання до лабораторної роботи № 23

1. Знайти частинний розв’язок лінійного однорідного рівняння.

2. Розв’язати задачу Коші.

Варіант	Завдання
1	1. . 2. а) б) .
2	1. . 2. а) б) .
3	1. , . 2. а) б) .
4	1. . 2. а) б) .
5	1. . 2. а) б) .
6	1. . 2. а) б) .
7	1. . 2. а) б) .
8	1. . 2. а) б) .
9	1. . 2. а) б) .
10	1. . 2. а) б) .
11	1. . 2. а) б) .
12	1. . 2. а) б) .
13	1. . 2. а) б) .
14	1. . 2. а) б) .
15	1. . 2. а) б) .
16	1. . 2. а) . б) .
17	1. . 2. а) . б) .
18	1. . 2. а) . б) .
19	1. . 2. а) . б) .
20	1. . 2. а) . б) .
21	1. . 2. а) . б) .
22	1. . 2. а) . б) .
23	1. . 2. а) . б) .
24	1. . 2. а) . б) .
25	1. . 2. а) . б) .
26	1. . 2. а) . б) .
27	1. . 2. а) . б) .
28	1. . 2. а) . б) .
29	1. . 2. а) . б) .
30	1. . 2. а) . б) .

Лабораторна робота № 24

Метод варіації. Системи диференціальних рівнянь.

Короткі теоретичні відомості.

Для знаходження розв’язків лінійних диференціальних рівнянь вищих порядків зі сталими коефіцієнтами зручним для використання є метод варіації, а для розв’язання систем диференціальних рівнянь − метод підстановки.

Приклад

Знайти загальний розв’язок лінійного неоднорідного диференціального рівняння із сталими коефіцієнтами: . Складемо характеристичне рівняння відповідного однорідного рівняння: _.

Обчислення в MathСad:

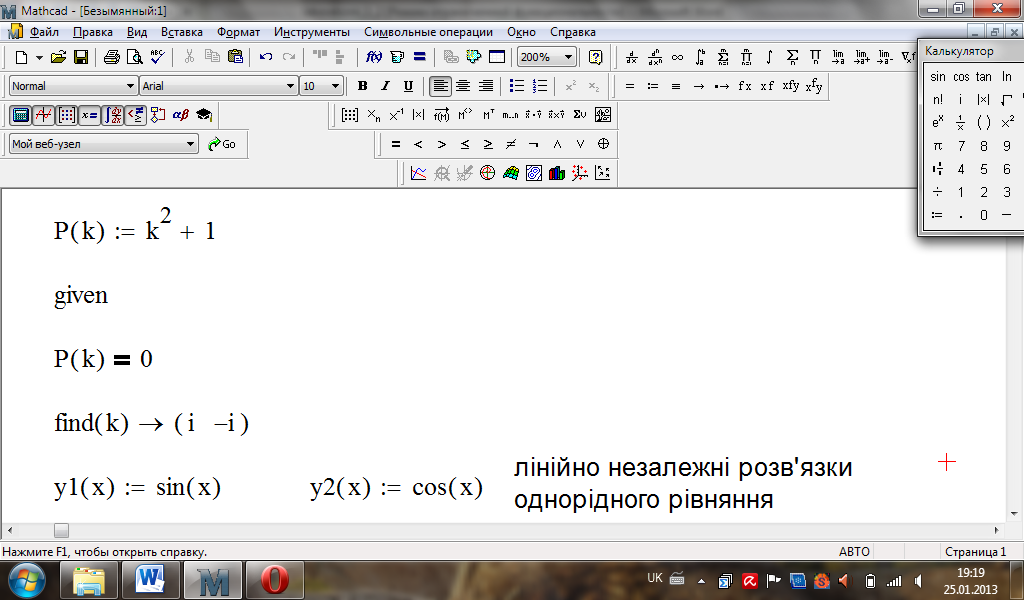
Шукаємо загальний розв’язок початкового рівняння у вигляді , де - невідомі функції. Позначивши , розв’язуємо систему засобами MathCad

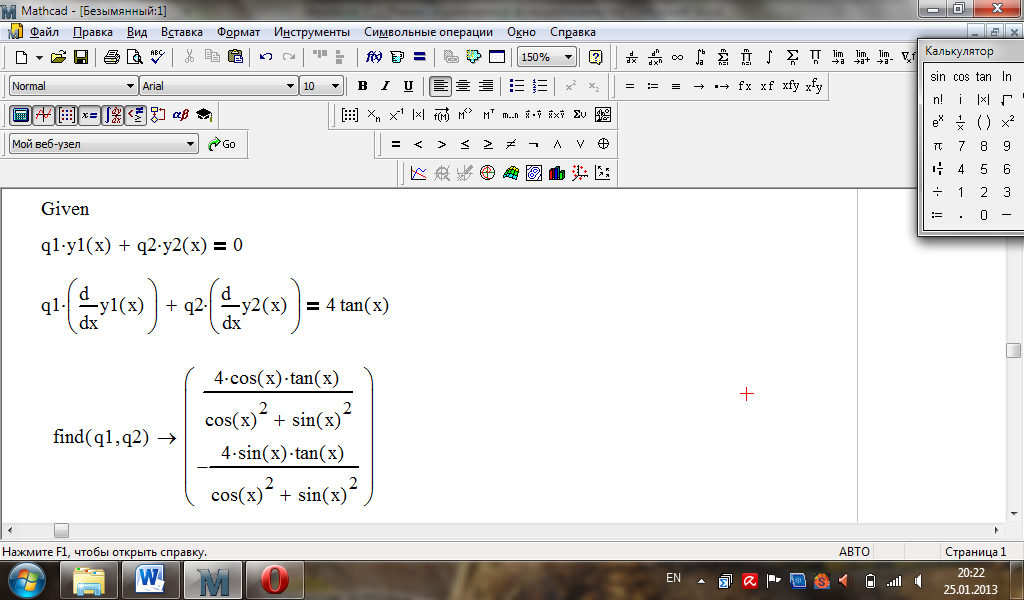
За допомогою оператора Simplify на панелі Symbolic спростимо обидва вирази, виділивши змінну .

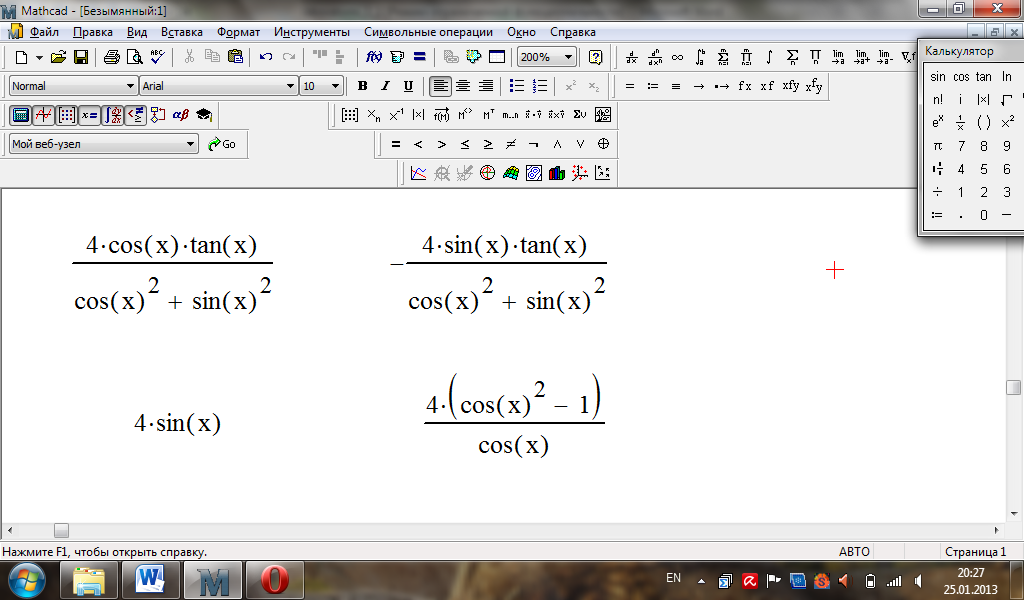
Знайдемо невідомі функції:

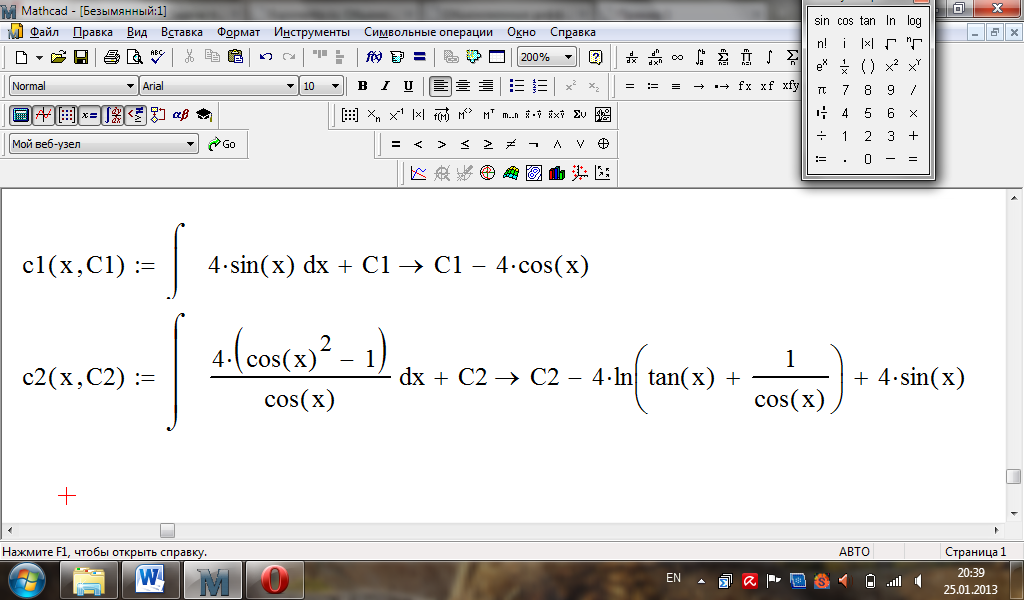
Загальний розв’язок рівняння: