Лабораторна робота № 19. Розв’язування диференціальних рівнянь першого порядку.

Приклад.

Розв’язати задачу Коші .

Розв’язання.

Після відокремлення змінних отримаємо:

Обчислення в MathСad:

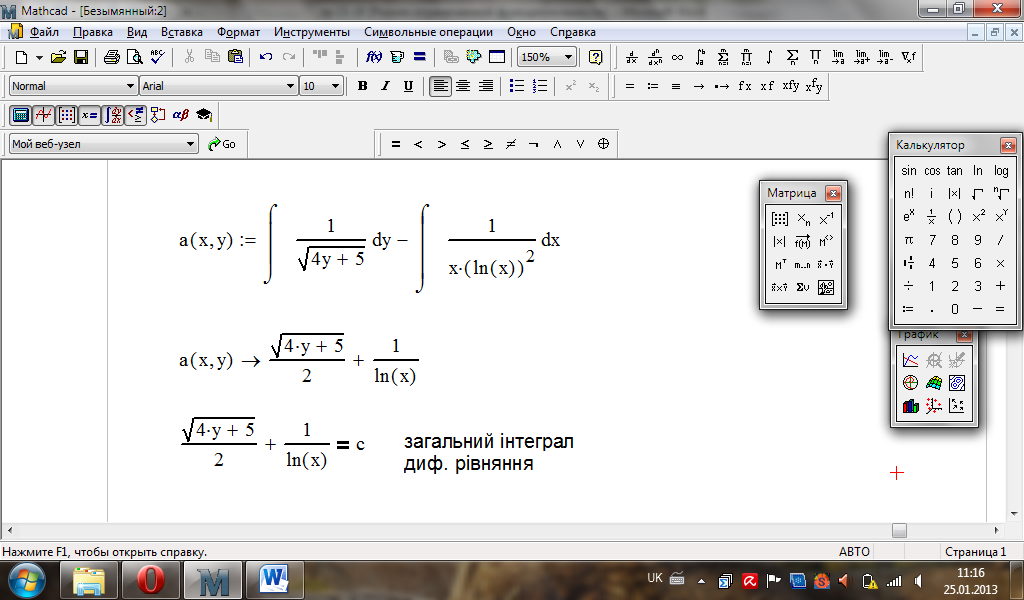
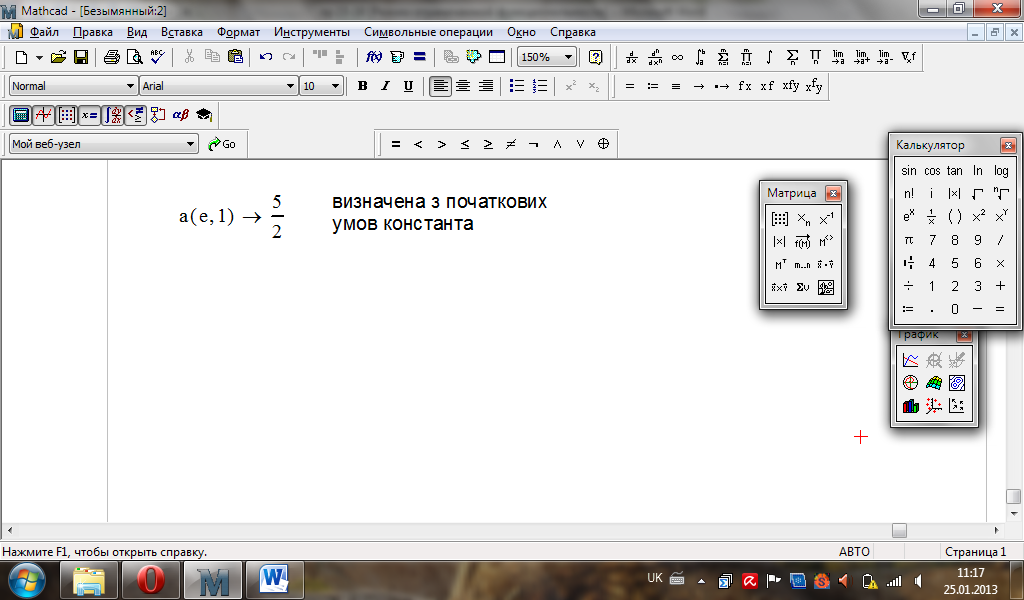
Виписуємо розв’язок задачі Коші:

Завдання до лабораторної роботи № 19.

1. Розв’язати задачу Коші для диференціального рівняння з відокремлюючими змінними

2. Знайти частинний розв’язок диференціального рівняння, наприкінці самостійно підібравши початкову умову.

3. Розв’язати диференціальне рівняння.

Варіант	Завдання
1	1. 2. 3.
2	1. 2. 3.
3	1. 2. 3.
4	1. 2. 3.
5	1. 2. 3.
6	1. 2. 3.
7	1. 2. 3.
8	1. 2. 3.
9	1. 2. 3.
10	1. 2. 3.
11	1. 2. 3.
12	1. 2. 3.
13	1. 2. 3.
14	1. 2. 3.
15	1. 2. 3.
16	1. 2. 3.
17	1. 2. 3.
18	1. 2. 3.
19	1. 2. 3.
20	1. 2. 3.
21	1. 2. 3.
22	1. 2. 3.
23	1. 2. 3.
24	1. 2. 3.
25	1. 2. 3.
26	1. 2. 3.
27	1. 2. 3.
28	1. 2. 3.
29	1. 2. 3.
30	1. 2. 3.

Лабораторна робота № 20. Однорідні диференціальні рівняння першого порядку. Короткі теоретичні відомості.

Для розв’язання задачі Коші в MathCAD передбачена функція ― Odesolve, яку потрібно визначити ключовим словом Given (Дані). Похідні в диференціальному рівнянні можна вводити за допомогою звичайного оператора похідної (на панелі інструментів Calculus (Матанализ)) або за допомогою комбінації клавіш <Ctrl+F7>, знак рівності в рівнянні та початкових умовах за допомогою комбінації клавіш <Ctrl+=>. Розв’язання диференціального рівняння закінчується функцією Odesolve (х, с, М), де – змінна інтегрування, – правий кінець інтервалу пошуку розв’язку (лівий визначається початковою умовою), – крок (кількість інтервалів), який впливає на точність. Функція Odesolve видає розв’язок задачі у вигляді функції, яка не має аналітичного представлення і може лише повернути числове значення розв’язку рівняння в довільній точці інтервалу.