Глава 2. Эконометрический анализ влияния социально-экономических факторов на уровень рождаемость с использованием панельных данных

2.1. Кластеризация регионов

Огромная территория нашей страны подразделена на множество регионов, каждый из которых имеет своё управление, свой климат, природные богатства, свой экономический и социальный потенциал, даже своё законодательство по отдельным вопросам. При этом для обеспечения территориально-административной целостности страны выгодно было бы, чтобы между российскими регионами не существовало чрезмерных различий в экономическом развитии и уровне жизни населения. Однако высокая дифференциация социально-экономических показателей регионов Российской Федерации все-таки существует.

Как правило, при работе с большим массивом данных на предварительном этапе исследования необходимо разбить всю совокупность данных на кластеры и выявить однородные группы для дальнейшего анализа.

В основу классификации регионов были положены показатели, которые не имели между собой статистически существенной связи, и поэтому включение каждого из них в число классообразующих признаков вполне оправдано. К этим показателям относятся: суммарный коэффициент рождаемости, число абортов, общие коэффициенты брачности, коэффициенты младенческой смертности.

Наилучшие в содержательном плане результаты показала классификация регионов РФ на 5 кластеров (однородных зон) с использова­нием метода k-средних и евклидовой метрики. Результаты кластеризации представлены в Приложении 2 (табл.2.1) . В первый кластер попали 6 регионов, во второй – 5, в третий – 20, в четвертый – 15, пятый кластер оказался самым многочисленным – 33 региона.

Наибольший интерес среди полученных кластеров представляет тот, к которому был отнесен Башкортостан, поэтому для дальнейшего исследования выбираем 2 кластер.

2.2. Эконометрическое моделирование социально-экономических факторов, оказывающих влияние на уровень рождаемости.

Для построения эконометрической модели было решено использовать панельные данные. Хотя панельные данные и имеют свои особенные проблемы с получением хороших оценок параметров, они, тем не менее, обеспечивают лучшую спецификацию моделей и объединяют пространственную и временную размерности в одну оценку. Основным преимуществом использования панельных данных является возможность учесть влияние ненаблюдаемых факторов для каждой единицы наблюдения, т.е. фиксированные эффекты, а также макроэкономические шоки, т.е. временные эффекты [10].

Первоначально все данные были прологарифмированы. Необходимо построить несколько моделей и затем на основе различных критериев выбрать наилучшую модель, проверить ее адекватность.

1) На первоначальном этапе была построена модель сквозной регрессии, в которой не учитываются ни фиксированные, ни случайные эффекты. Оценки такой модели соответствуют оценкам, полученным МНК. Результаты исходной модели с полным набором факторов представлены в Приложении 3 (табл.2.2). Некоторые переменные оказались незначимы, их необходимо удалить. Таким образом, окончательная модель примет следующий вид (Приложение 3 табл.2.3):

Низкое значение свидетельствует о том, что модель плохо описывает данные, потому что в ней не учтены ни фиксированные, ни случайные эффекты.

2) Модель со случайным индивидуальным эффектом отражает влияние пропущенных и ненаблюдаемых переменных, характеризующих индивидуальные особенности исследуемых объектов. Оценивание модели с полным набором факторов представлено в Приложении 4 (табл.2.4). Незначимые факторы также были исключены из оценивания и модель приняла следующий вид (Приложение 4 табл.2.5):

где EY –эффект года.

Полученная модель обладает высоким значением коэффициента детерминации . Однако, следует отметить, что данная регрессия оценивается с помощью обобщенного МНК, а значит не может служить адекватной мерой оценки полученного уравнения. Значимость данного уравнения подтверждается на основе .

3) Модель с детерминированными индивидуальными и временными эффектами. В данном случае в регрессию включаются дополнительные коэффициенты, соответствующие отдельному объекту, либо периоду, включающие в себя влияние набора факторов, не учтенных в рамках модели.

Результаты оценивания данной модели представлены в Приложении 5 (табл.2.6). После удаления незначимых факторов модель принимает следующий вид (Приложение 5 табл.2.7):

Коэффициент детерминации полученной модели существенно возрос по сравнению с двумя предыдущими моделями . Значимость уравнения в целом отражает значение F-статистики: . Можно выдвинуть предположение о том, что данная модель описывает наши данные лучше, чем предыдущие. Однако возникает необходимость в проверке целесообразности введения временных и случайных эффектов в построенные модели.

Для этого рассмотрим тест Хаусмана, который позволяет сделать выбор между моделями с фиксированными и случайными эффектами. Тестируется независимость случайных эффектов и набора объясняющих факторов, то есть если случайный эффект сильно коррелирован с регрессорами, то наиболее адекватна данным модель с детерминированными эффектами.

По результатам данного теста (Приложение 7 табл.2.10) можно сделать вывод о том, что на основе значений р-уровня нулевая гипотеза об отсутствии связи между индивидуальными и зависимыми переменными отвергается (табл.2.9), значит, необходимо выбрать модель с фиксированными эффектами.

Таблица 2.9

Тест Хаусмана для модели со случайным индивидуальным эффектом

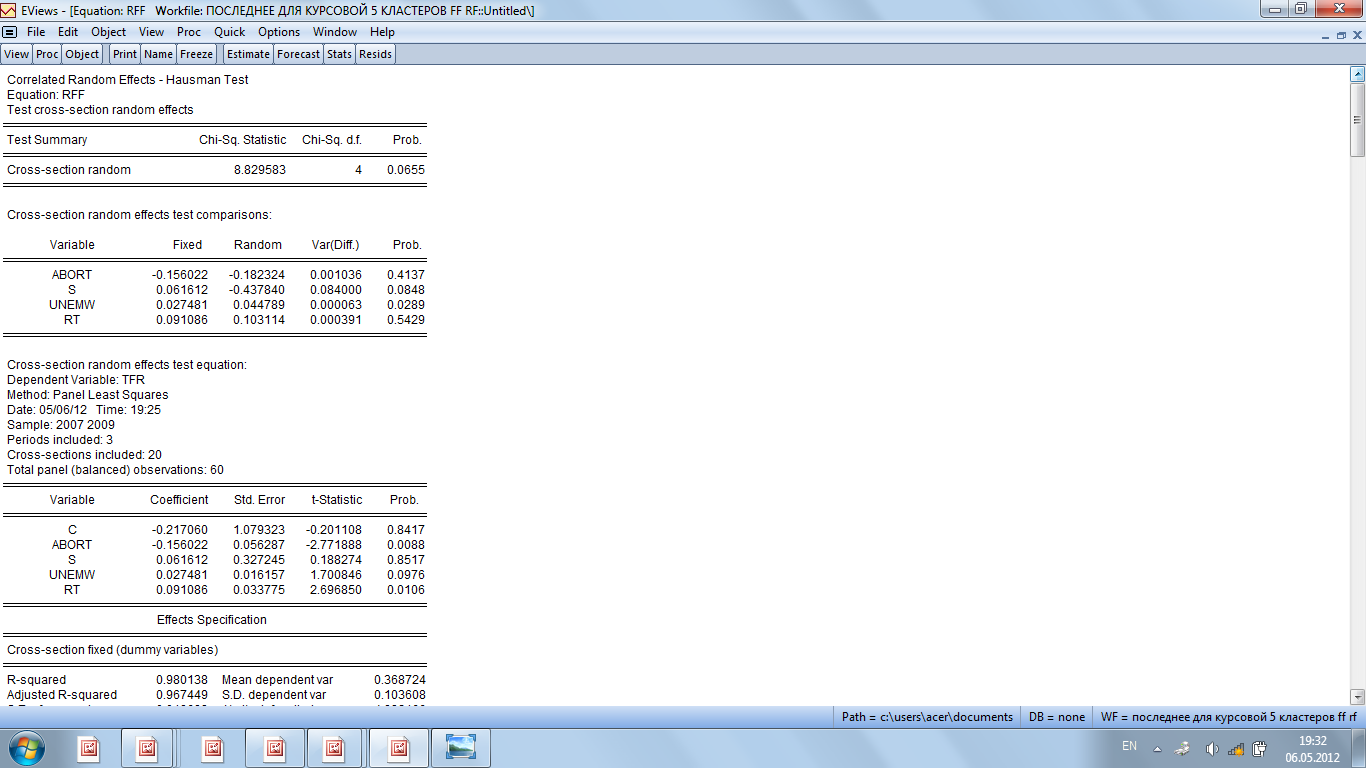
Теперь возникает необходимость проверки значимости временных эффектов (Redundant Fixed Effects) для того, чтобы сделать окончательный выбор между моделью сквозной регрессии и моделью с фиксированными эффектами.

Результаты данного теста, представленные в Приложении 6 (табл.2.8), свидетельствует о том, что необходимо выбирать модель с детерминированными эффектами, а не модель сквозной регрессии (табл.2.11), т.к. нулевая гипотеза о том, что эффекты являются «лишними» отвергается. Вывод о правомерности включения детерминированных эффектов сделан на основе значимой F-статистики и статистики для эффекта субъекта и для эффекта года.

Таблица 2.11

Тест на значимость индивидуальных и временных

детерминированных эффектов

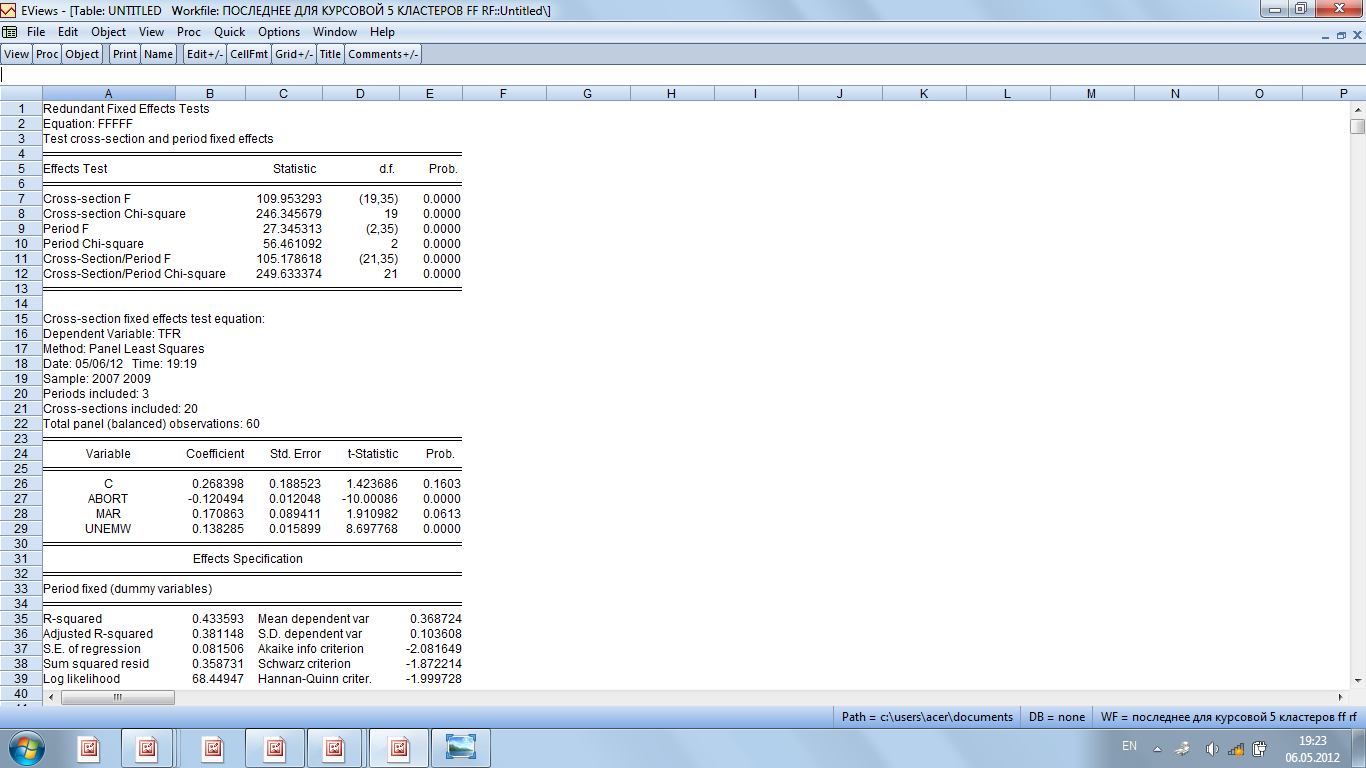
Исходя из представленных тестов, делаем вывод о том, что лучшей из трех построенных моделей является модель с фиксированными эффектами. Таким образом, окончательная модель имеет следующий вид:

Наряду с общим фиксированным эффектом существуют и отдельные индивидуальные эффекты, характерные для каждого региона в отдельности.

Эти факторы могут быть не наблюдаемыми, но они оказывают существенное влияние на исследуемый показатель, например, географическое положение, история, культурные традиции и другое.

В таблице 2.12 все регионы были проранжированы по величине индивидуальных фиксированных эффектов:

Таблица 2.12

Индивидуальный фиксированный эффект для каждого региона

№	Субъект	Индивидуальный эффект
1	г, Санкт-Петеpбуpг	-0,145389
2	Муpманская область	-0,098938
3	Ростовская область	-0,097327
4	Белгородская область	-0,090393
5	Воронежская область	-0,084431
6	Саратовская область	-0,080071
7	Московская область	-0,08007
8	Томская область	-0,049436
9	Рязанская область	-0,041072
10	Ставропольский край	-0,019332
11	Алтайский край	-0,011709
12	Краснодарский край	0,034162
13	Красноярский край	0,03741
14	Республика Адыгея	0,052374
15	Республика Маpий Эл	0,063148
16	Челябинская область	0,075694
17	Астраханская область	0,099407
18	Республика Башкортостан	0,115653
19	Удмуртская Республика	0,134129
20	Забайкальский край	0,186191

Наибольшие значения фиксированных эффектов наблюдаются в Забайкальском крае, Удмуртской Республике и Республике Башкортостан, возможно, это связано с хорошей экологической обстановкой в данных регионах. Наименьшие значения – в г.Санкт-Петербург, Мурманской и Ростовской области, это значит, что в данных регионах присутствуют неблагоприятные факторы, которые отрицательно воздействуют на уровень рождаемости.

Помимо индивидуальных эффектов, можно исследовать и временные эффекты, представленные в таблице 2.13:

Таблица 2.13

Временные эффекты

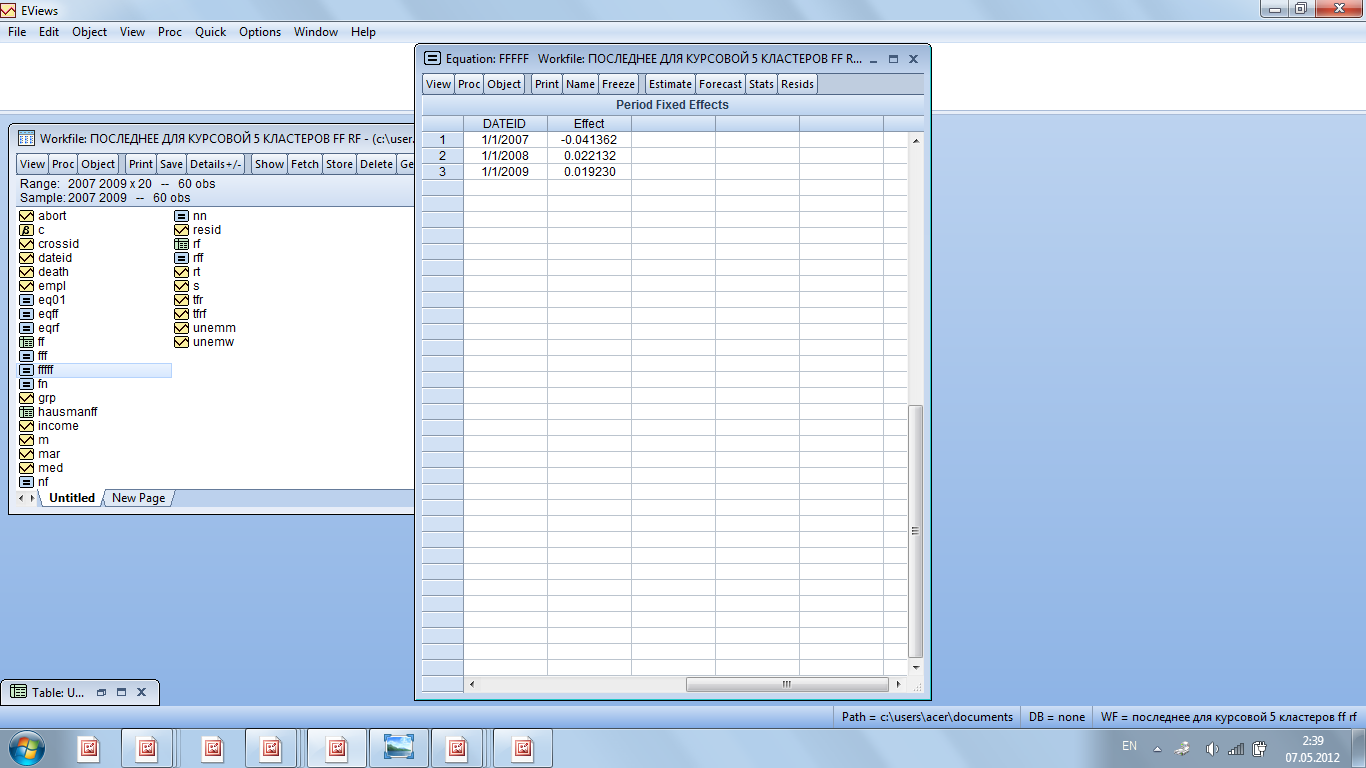
В 2007 году наблюдается негативное влияние ненаблюдаемых факторов на исследуемый показатель, в 2008 и в 2009 годах – положительное влияние.

Анализ адекватности моделей панельных данных состоит в проверке соответствия распределения остатков нормальному закону. Для этого была построена гистограмма остатков полученной модели (Приложение 8 рис.1).

Значение статистики Харке-Бера позволяет сделать вывод о том, что остатки модели имеют нормальное распределение.

Высокое значение коэффициента детерминации свидетельствует о хорошем качестве подгонки уравнения. Полученное значение позволяет сделать вывод о статистической значимости полученного уравнения в целом.

Следует отметить и то, что построенная модель хорошо описывает исходные данные (Приложение 8 рис.2).

Указанные выше факты позволяют сделать вывод об адекватности эконометрической модели, значит, ее можно использовать для прогнозирования.