4. Динамика материальной точки. Дифференциальные уравнения. Общие теоремы динамики точки.

Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил. Первый закон Ньютона. Инерциальные системы отсчета Формулировка первого закона Ньютона такова: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба названных состояния отличаются тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело других тел не вызовет ее изменения. Масса и импульс тела Воздействие на данное тело со стороны других тел вызывает изменение его скорости, т. е. сообщает данному телу ускорение. Опыт показывает, что одинаковое воздействие сообщает разным телам разные по величине ускорения. Всякое тело противится попыткам изменить его состояние движения. Это свойство тел называется инертностью. В качестве количественной характеристики инертности используется величина, называемая массой  тела. Чтобы определить массу некоторого тела, нужно сравнить ее с массой тела, принятого за эталон массы. Можно также сравнить массу данного тела с массой некоторого тела, уже определенной путем сравнения с эталоном. Система тел, взаимодействующих только между собой и не взаимо­действующих с другими телами, называется замкнутой. Если заставить эти частицы взаимодействовать (например, столкнуть), их скорости изменятся на величины . Опыты показывают, что эти изменения всегда имеют противоположные направления, т. е. отличаются знаком. Отношение же модулей изменения скоростей не зависит от способа и интенсивности взаимодействия данных двух тел. Это отношение принимается равным обратному отношению масс рассматриваемых тел:

(1) т.е. более инертное тело (с большей массой) претерпевает меньшее изменение скорости. Приняв во внимание противоположное направление векторов изменения скорости, соотношение (1) можно написать в виде:

(2)

Произведение массы тела на его скорость называется импульсом тела (по-старому - количество движения). Обозначив импульс буквой р, получим:

(4)

Определение (4) справедливо для материальных точек и протяженных тел, движущихся поступательно.

Заменив в (3) произведения массы на скорость импульсами, придем к соотношению , или . Если изменение какой-то величины равно 0, это означает, что величина остается постоянной. Т.о., мы пришли к выводу, что полный импульс замкнутой системы двух взаимодействующих частиц остается постоянным:

(6)

закон сохранения импульса.

Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на тело силе:

(9)

и уравнение (9) называется уравнением движения тела.  Заменив согласно (4) импульс тела и учтя, что в классической механике масса предполагается постоянной, можно записать, что

(10)

Т.о., более распространенная формулировка закона Ньютона: произведение массы тела на его ускорение равно действующей на тело силе. Соотношение (10) вызывает достаточно много споров, и общепринятого толкования этого соотношения до сих пор нет, потому что не существует независимых способов определения массы и силы, входящих в выражение (10). Третий закон Ньютона утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению, т.е.

(11)

Из третьего закона Ньютона вытекает, что силы возникают попарно: всякой силе, приложенной к какому-то телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу, взаимодействующему с данным. Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений. Уравнения в декартовых координатах. Из кинематики известно, что движение

точки в прямоугольных декартовых координатах задается уравнениями :

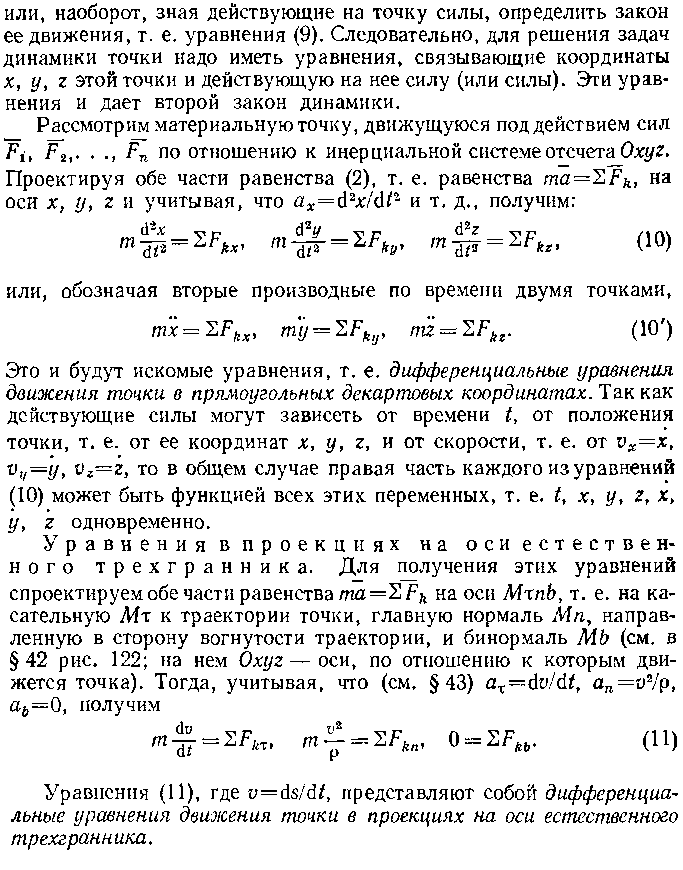Так как масса точки постоянна, а ее ускорение a—dv/dt, то уравнение (2), выражающее основной закон динамики, можно представить в виде

теорема об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток вре­мени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени. теорема моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого- нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.

5. Механическая система твёрдых тел. Звенья, кинематические пары, кинематические цепи. Классификация.

Систему материальных точек или тел, движение (или равновесие) которой рассматривается, называют механической системой. Кинематическая пара (англ. kinematic pair) — это соединение двух звеньев, обеспечивающее определённое относительное движение. Для всех кинематических пар необходим постоянный контакт между их элементами, это достигается либо с помощью определённых усилий, либо приданием элементам определённой геометрической формы. Классификация: По числу связей на относительное движение: от одной до пяти связей. Это связано со степенями свободы, которых для материального тела всего шесть; исключая (связывая) по одной, мы получаем пять вариантов связей. По контакту между звеньями: высшие (контакт по точке или линии); низшие (контакт по поверхности). Кинематическая цепь (англ. kinematic chain) — это связанная система объектов, образующих между собой кинематические пары. Кинематические цепи имеют такую классификацию: Простые и сложные. В простой кинематической цепи каждое из ее звеньев входит в состав одной или двух кинематических пар, а в сложной кинематической цепи имеются звенья, входящие в состав трех и более кинематических пар. Открытые и замкнутые. В открытой (незамкнутой) кинематической цепи имеются звенья, входящие в состав одной кинематической пары, а в замкнутой цепи каждое звено входит в состав 2-х и более кинематических пар. Плоские и пространственные. Если точки всех звеньев кинематической цепи двигаются в одной или параллельных плоскостях, то такая кинематическая цепь называется плоской, в противном случае кинематическая цепь — пространственная, так как точки её звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые. Если между точками (телами) механической системы действуют силы взаимодействия, то она обладает тем свойством, что в ней положение или движе­ние каждой точки (тела) зависит от положения и движения всех остальных. Классическим примером такой системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Действующие на механическую систему активные силы F и реакции связей N_k разделяют на внешние F и внутренние F. Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. Это разделение является условным и зависит от того, какая механическая система рассматривается. Например, если рассматривается движение всей Солнечной системы, то сила притяжения Земли к Солнцу будет внутренней; если же рас­сматривается движение системы Земля — Луна, то для этой системы та же сила будет внешней.