§ 5. Тройной интеграл.

Пусть Х - некоторое ограниченное измеримое множество точек пространства (“тело” ), f (х,у,z) – функция, определённая и ограниченная на Х, а τ = дробление этого множества. Запишем интегральные суммы функции f по дроблению τ :

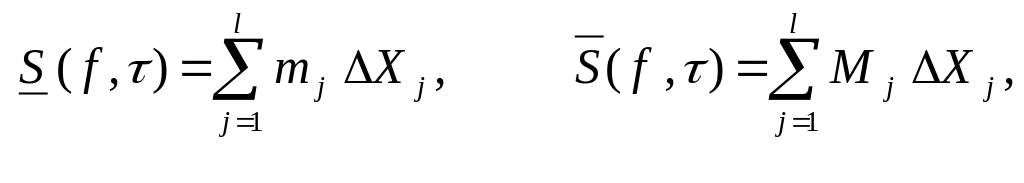S( f ,τ)= . Здесь m_j и M_j –точная нижняя и точная верхняя грани функции f на X_j , P_j(x_j,y_j,z_j) – точка, принадлежащая X_j, а Δ X_j – обьём множества X_j: Δ X_j = μ₃ (X_j). Если f интегрируема на множестве Х, а { τ_n} - нормальная последовательность дроблений этого множества, то последовательности интегральных сумм и сходят- ся и имеют общий предел – интеграл от f (х,у,z) по множеству Х . Интеграл от фун- кции трёх переменных f (х,у,z) называют тройным интегралом и обозначают символом Итак, если f (х,у,z) интегрируема на множестве Х, то

, где { τ_n} -любая нормальная последовательность дроблений множества Х.

5.1. Выражение тройного интеграла через повторный

Пусть В - некоторое множество, плоская фигура, функции и определены на В , причем на В. Обозначим:

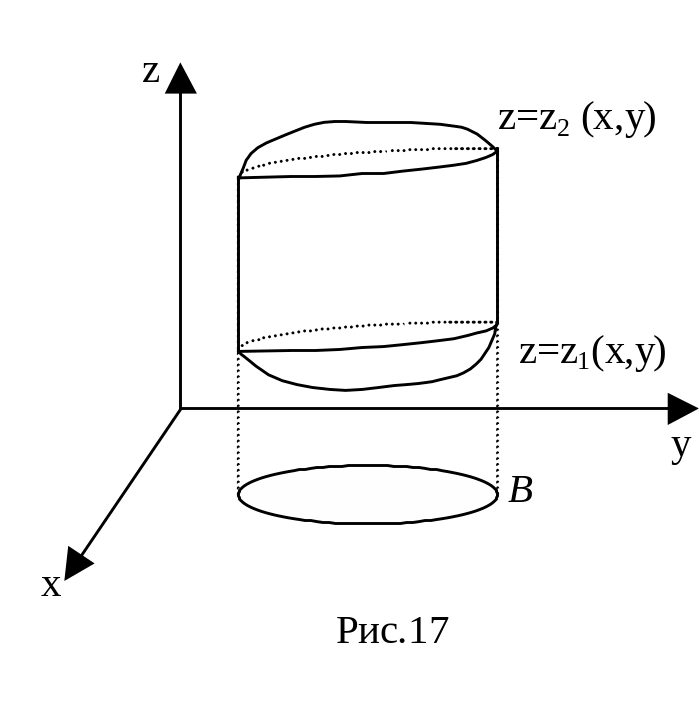
. Множество такой структуры будем называть прос- тым относительно оси OZ, а фигуру В – проекцией множества Х на плоскость ХОУ (Рис.17) . Анало- гично можно определить множества в , простые относительно координатных осей ОХ и ОУ.

Теорема 2. ( О равенстве между тройным и повторным интегралами) Пусть -множество, простое относительно оси OZ , проекция которого В на плоскость ХОУ есть плоская фигура, простая относительно оси ОУ :

.

Если у₁(х) и у₂(х) непрерывны на [a,b], и непрерывны на В, а f(x,y,z) – функция, непрерывная на Х, то справедливы равенства

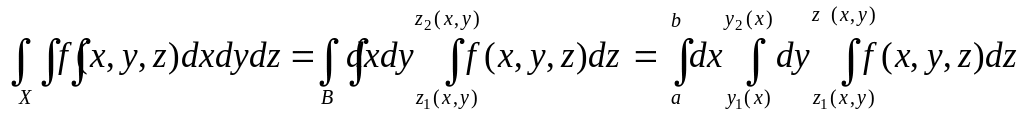
► Так как f непрерывна на замкнутом ограниченном множестве Х, она интегрируема на нём.

*) Пусть сначала f неотрицательна на Х. В этом случае справедливо равенство , где

(см. свойство 4, п.3.2). Сегмент [a,b] является проекцией на ось ОХ подграфика . Пусть ξ –некоторая точка на [a,b], -сечение подграфика , а - проекция этого сечения на координатное подпространство (y,z,u):

,

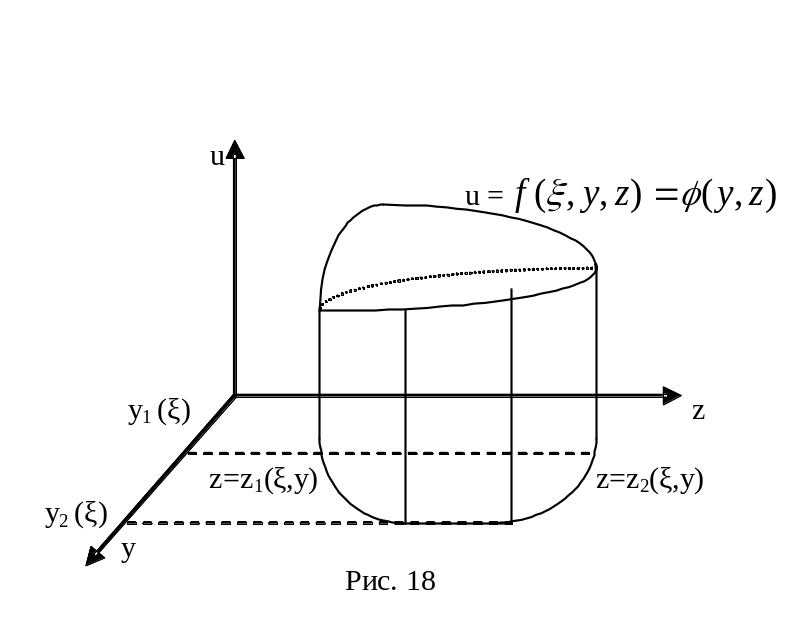( рис.18 ). Множества и замкнуты, а потому и измеримы. Кроме того, они конгруентны; значит, . Множество явля-ется подграфиком функции φ(y,z) = = f(ξ,y,z) на простой относительно оси OZ плоской фигуре, ограничен- ной прямыми , и кривыми и (см. рис.18); поэтому

)= .

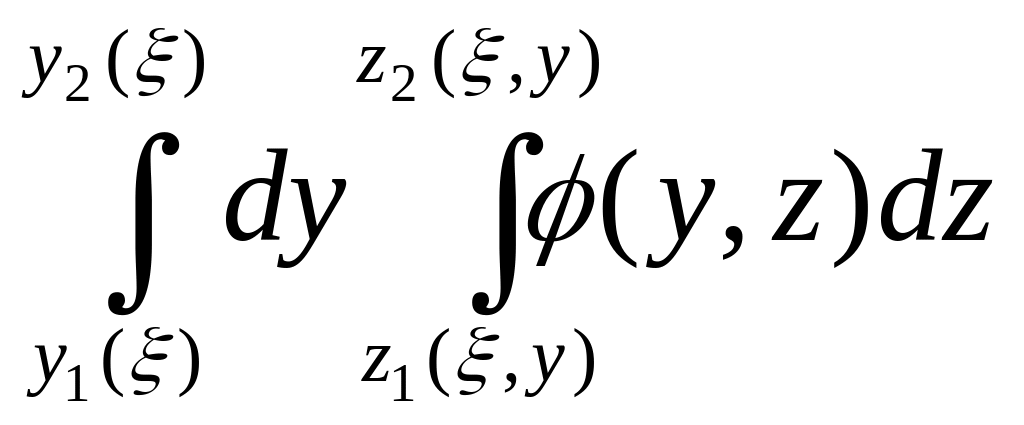На [a,b] определим функцию σ( ), положив при каждом ξ , принадле- жащем [a,b] , σ(ξ) равным обьёму сечения : σ(ξ) ). Эта функция непрерывна на [a,b]. В самом деле, ) = )= .

Теперь непрерывность σ(ξ) на [a,b] можно вывести из теорем о непрерывности определенных интегралов, зависящих от одного и нескольких параметров. Заменив обозначение ξ на х, получим: при каждом х на [a,b]

σ(х) = 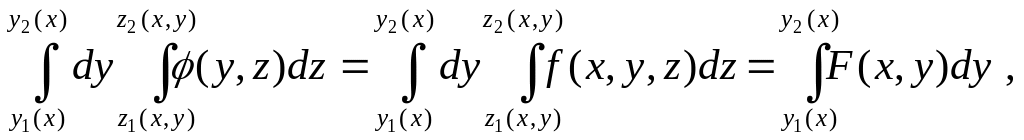где 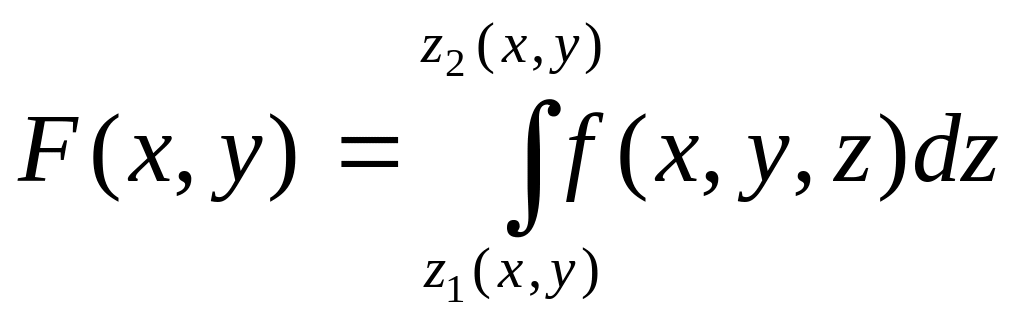. Так как и непрерывны на В, а f(x,y,z) – функция, непрерывная на Х, то F(x,y) непрерывна на В ( см. теорему о непрервыности интегралов, зависящих от нескольких параметров). Так как у₁(х) и у₂(х) непрерывны на [a,b], а F(x,y) непрерывна на В, то по теореме о непрерывности интеграла, зависящего от одного параметра 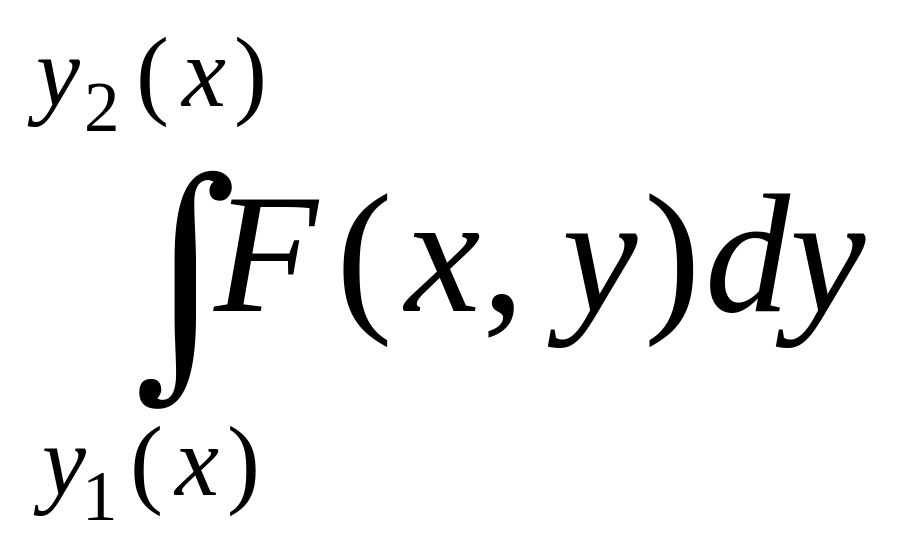есть функция параметра х, непрерывная на [a,b].

Итак, σ(х) непрерывна, а, следовательно, и интегрируема на [a,b].По теореме п. 3.5

.

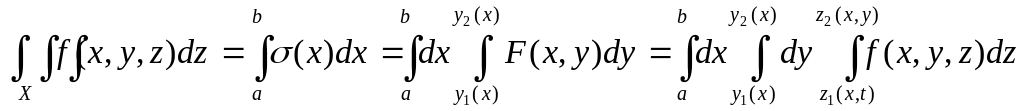**) Пусть теперь f - любая непрерывная на Х функция. Её неотрицательные состав- ляющие f и f непрерывны и неотрицательны на Х. По доказанному выше

;

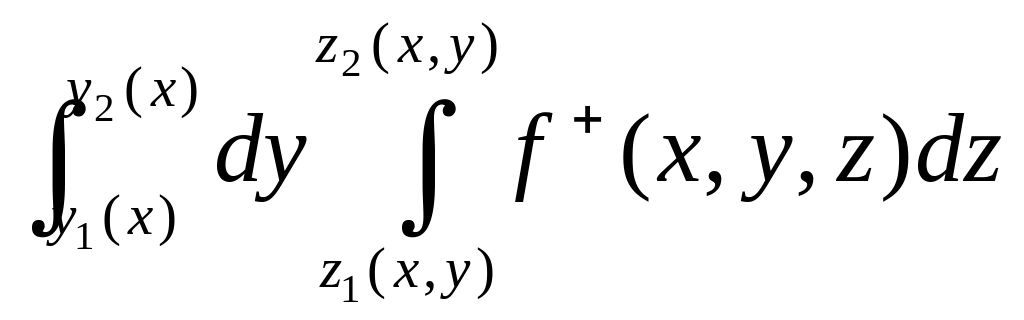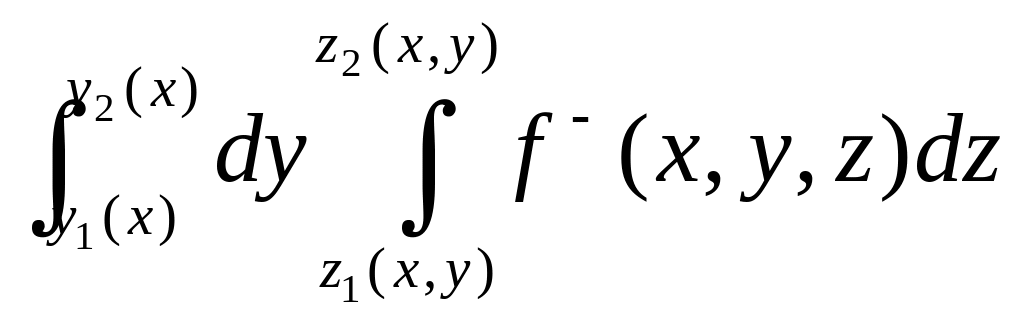; Отсюда:

=

=

= - = = . ◄

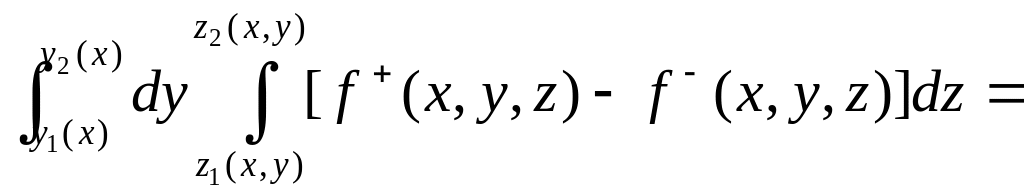
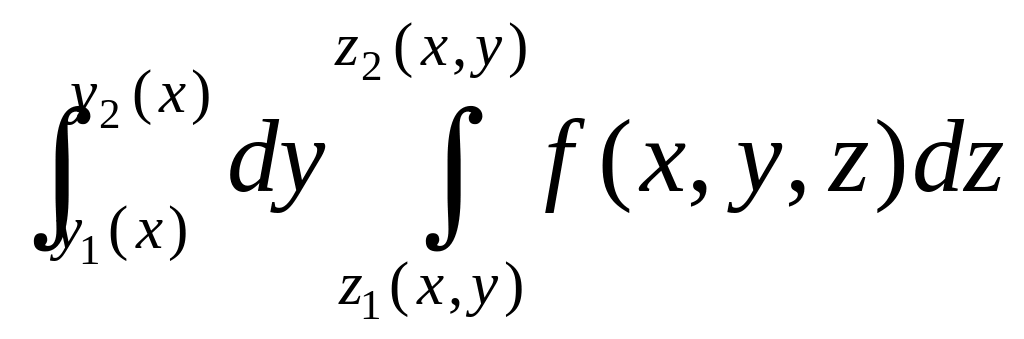Замечание. Пусть , где В – фигура простая относительно оси ОХ: . Если и непрерывны на и выполнены другие условия доказанной теоремы, то

.

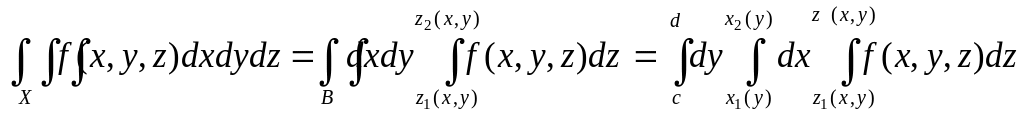Пример. Вычислить , где Х - область, ограниченная координат- ными плоскостями и плоскостью x+y+z = 1(рис.19. ). Множество Х является простым

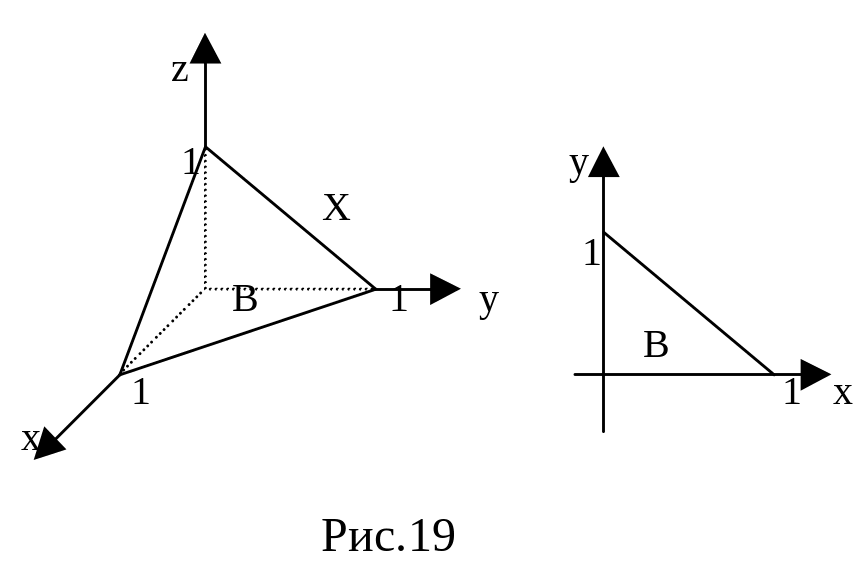
относительно оси аппликат, причём

z₁ (x,y) ≡ 0, z₂ (x,y) = 1-x-y.

Запишем равенство между тройным и повторным интегралами:

= , где В – треугольник, отсечённый от первого координатного угла плоскости ХОУ прямой х+у =1 (рис. 19). Заменив двойной интеграл повторным, получим:

=

= - = = = =

5.2. Отображения множеств в пространстве .

Пусть - некоторое множество, U(x,y,z), V(x,y,z) и W(x,y,z) – некоторые функ- ции, определенные на G, а Φ: - отображение множества G, при котором каждой упорядоченной тройке (x,y,z) сопоставляется упорядоченная тройка (u,v,w), где u = =U(x,y,z) , v = V(x,y,z) , w = W(x,y,z) Мы будем говорить, что отображение Φ задано системой уравнений

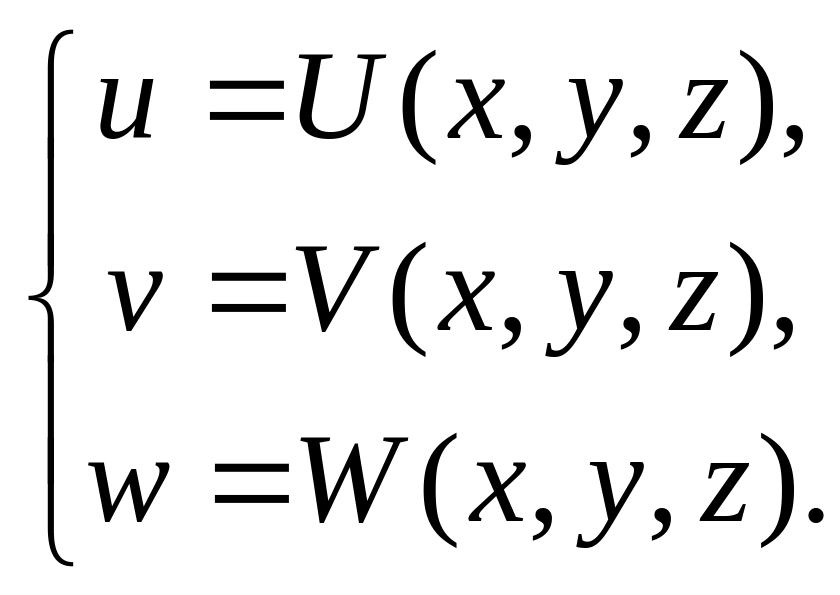(1) Тройки (x,y,z) и (u,v,w) будем считать декартовыми прямоугольными координатами точек Р и Р* соответственно: Р(x,y,z) , Р*(u,v,w). Р* будем называть образом точки Р при ото- бражении Φ, а Р – прообразом точки Р* при отображении Φ, и будем записывать Р*= =Φ(Р). Совокупность { Р*} образов всех точек множества G назовём образом множества G при отображении Φ, обозначим её через G*. Будем говорить,что Φ отображает G на G* и при этом записывать G*= Φ(G).

Отображение Φ называют взаимно однозначным, если образы двух различных между собой точек множества G обязательно различны между собой: если Р₁ ≠ Р₂ , то Р₁*≠ Р₂*.

Пусть отображение Φ, заданое системой уравнений (1), взаимно однозначно, и пусть G*= Φ(G). В этом случае для каждой точки Р* * в множестве G существует и при том только один прообраз Р. Это обстоятельство позволяет рассмотривать отображе- ние множества G*, при котором каждой точке Р* * сопоставляется точка Р - про- образ Р*при отображении Φ . Это отображение назовём обратным отображению Φ и бу- дем обозначать его через Φ . Отображение Φ является взаимно однозначным, а обрат- ное ему отображение есть Φ: (Φ ) = Φ ; отображения Φ и Φ - это пара взаимно обрат- ных отображений (рис.20). Заметим: Φ ( Φ(Р)) =Р ; Φ(Φ (Р*)) =Р*.

z

w

G G*

Φ

P=Φ (P*) P*=Φ(P)

Ψ= Φ

y

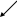x v

Рис. 20. u

Пусть система (1) задает взаимно однозначное отображение Φ , и пусть G*= Φ(G) . Определим на множестве G* функции Х(u,v,w ) , Y(u,v,w ) и Z(u,v,w), значения которых в произвольной точке Р*( u,v,w ) * есть соответственно абсцисса х и ордината у её прообраза Р(х,у,z): Х(u,v,w )= х, Y(u,v,w ) = у, Z(u,v,w)=z. Система уравнений

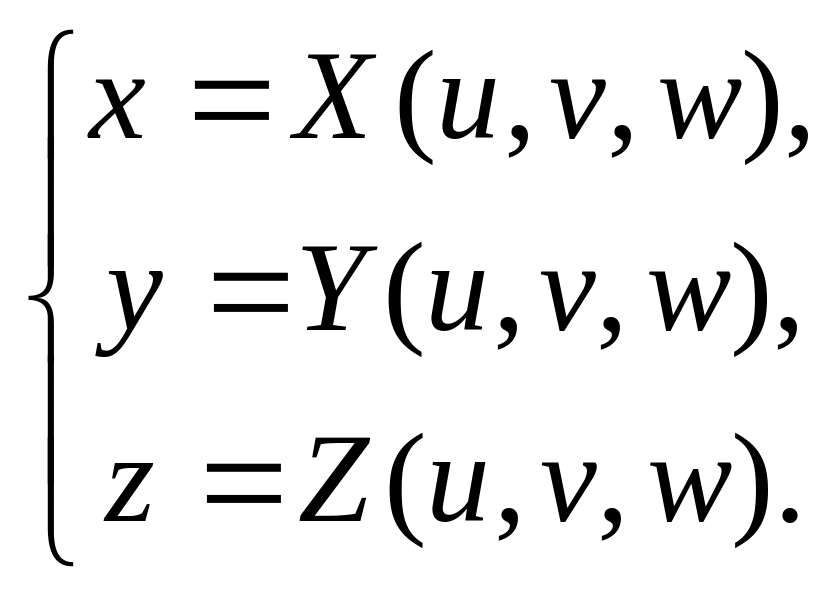(2) задаёт отображение Ψ множества G* , при котором каждой точке Р* * сопоставляет- ся её прообраз Р при отображении Φ ; а это означает, что Ψ= Φ .

Пусть отображения Φ и Ψ, заданные соответственно системами (1) и (2) представ ляют собой пару взаимно обратных отображений. Тогда Ψ (Φ(Р)) =Р. Отсюда следует, что функции U(x,y,z) , V(x,y,z) и W(x,y,z), координаты точки Р*= Φ(Р), удовлет- воряют на множестве G системе (2):

x ≡ X ,

y ≡ Y , (3)

z ≡Z . Аналогично, из Φ(Ψ (Р*)) =Р* вытекает, что функции Х(u,v,w ), Y(u,v,w ) , Z(u,v,w) образуют решение системы (1) на множестве :

Замечание. Пусть взаимно однозначное отображение Φ эадано системой (1). Что- бы записать систему, задающую обратное отображение Φ , нужно разрешить уравнения (1), выразить х , у и z через u, v и w.

Отображение Φ, заданное системой (1), называют непрерывным (дифференцируе- мым, непрерывно дифференцируемым) на множестве G, если функции U(x,y,z) , V(x,y,z) и W(x,y,z) непрерывны (соответственно дифференцируемы, непрерывно дифференцируемы) на множетве G.

Пусть отображение Φ, заданное системой (1), дифференцируемо на множестве G. Введем обозначение:

J_Φ(Р) = J_Φ (x,y,z) = Этот функциональный определитель называют якобианом отображения Φ. Если отобра- жение Ψ, заданное системой (2), дифференцируемо на G*, то

J_Ψ (Р*) = J_Ψ (u,v,w) =

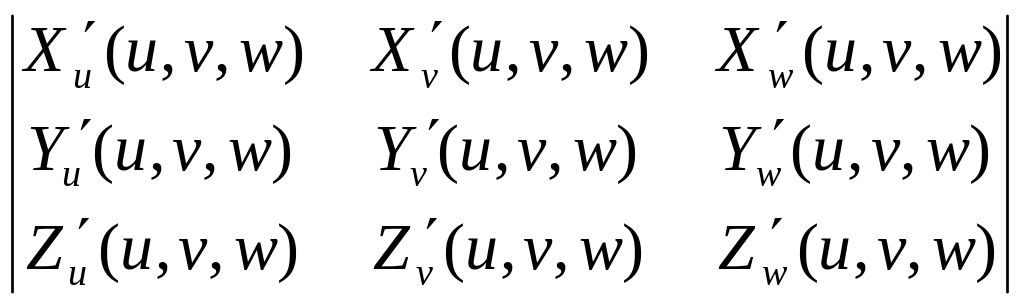
Теорема . ( O якобиане взаимно однозначного отображения)

Пусть G и G* -открытые множества в , и пусть отображение Φ, заданное систе- мой (1), взаимно однозначно отображает G на G*. Если Φ и обратное ему отображение Ψ = Φ дифференцируемы соответственно на G и на G*, то

1) J_Φ(Р) ≠ 0 ; J_Ψ (Р*) ≠ 0 ;

2) J_Φ (Р) = , где Р*= Φ (Р).

Доказательство проводится по той же схеме, что и доказательство аналогичной теоремы в п. 4.2.

5.3. Система координат в пространстве , её координатные поверхности и

координатные линии

Пусть G - некоторое множество точек пространства, т.е. (случай G= не исключён). Мы будем говорить, что на множестве G введена система координат UVW , если тем или иным способом каждой точке поставлена в соответствие упорядочен- ная тройка чисел (u,v,w), причём различным между собой точкам соответствуют обяза- тельно различные между собою упорядоченные тройки. Если точке Р соответствует трой- ка (u,v,w) , то мы будем записывать Р(u,v,w) , а числа u , v и w называть координатами точ- ки Р в системе координат UVW .

Пусть на множестве G введена система координат UVW. Выберем некоторое число p и обозначим через геометрическое место всех тех точек множества G, первая коорди- ната которых равна p : = {P(u ,v,w)| u = p}. Геометрическое место называют коорди- натной поверхностью системы координат UVW . Придавая p различные значения, мы бу- дем получать различные координатные поверхности. Обозначим через { } множество ( семейство) координатных поверхностей при всех возможных для множества G значени- ях первой координаты u. Ясно, что через каждую точку множества G проходит одна из координатных поверхностей этого семейства, и что при p₁ ≠ p₂ координатные поверхно- сти и не имеют общих точек.

Аналогично определим координатные поверхности и :

= {P(u ,v ,w)| v = q} , = {P(u_, v,w)| w = r} (здесь q и r - некоторые заданные числа), а также семейства { } и { } таких поверх- ностей.

Итак, если на множестве G введена система координат UVW , то на этом множестве определены три семейства координатных поверхностей { },{ } и { }. Любые две координатные поверхности, принадлежащие одному семейству, не имеют общих точек; через каждую точку множества G проходит по одной координатной поверхности каждого семейства; координатные поверхности , и имеют только одну общую точку P(u₀, v₀ ,w₀)

Линию, по которой пересекаются две координатные поверхности, принадлежащие разным семействам, называют координатной линией системы координат UVW. Всего име- ется три семейства координатных линий – линии пересечения поверхностей, принадлежа- щих семействам { }и { }, семействам { }и { }, семействам { } и { }.

Пусть S – некоторая поверхность, лежащая в G. Уравнение F(u,v,w) = 0 называют уравнением повегхности S в системе координат UVW , если точка Р(u,v,w) принадлежит S тогда и только тогда, когда её координаты (u,v,w) удовлетворяют этому уравнению. Урав- нения в системе UVW её координатных поверхностей , и есть u - u₀ = 0 , v - v₀ = = 0 и w - w₀ = 0 соответственно.

П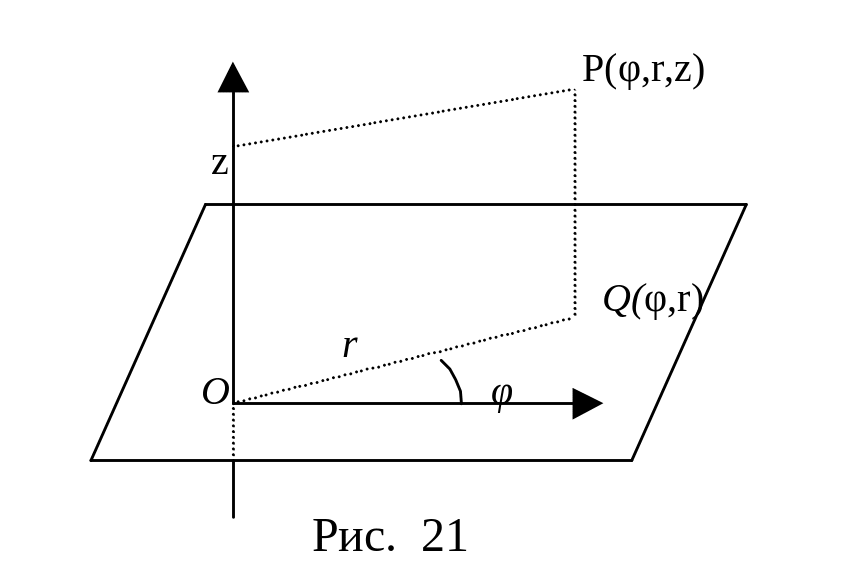 ример 1. Пусть в пространстве введена декартова прямоугольная система коор- динат XYZ. Плоскости, перпендикулярные оси абсцисс составляют семейство координат- ных поверхностей этой системы. Два другие семейства составляют плоскости, перпенди-- кулярные осям ординат и аппликат. Две плоскости, одна из которых перпендикулярна оси абсцисс, а другая –оси ординат пересека- ются по прямой, параллельной оси аппликат; следовательно, одно из семейств координат- ных линий составляют всевозможные пря- мые, параллельные оси аппликат.

Пример 2. Другой распространённой системой координат в проствранстве являет- ся система цилиндрических координат. В пространстве выбрана точка О, через неё проведена плоскость и числовая ось OZ пер- пендикулярно плоскости ( рис.21). На плоскости введена полярная система координат с полюсом О. Пусть Р – произвольная точка пространства, не лежащая на OZ . Из этой точки опускаем перпендикуляры на плоскость и на числовую ось. Пусть Q – основание перпендикуляра, опущенного на плоскость, а (φ, r) – полярные координаты этой точки; пусть z – координата на числовой оси основания перпендикуляра, опущенного на эту ось. Упорядоченную тройку чисел (φ, r ,z) называют цилиндрическими координатами точки Р. Координатная поверхность такой системы, определяемая уравнением φ = φ₀ - это полуплоскость, проходящая через ось OZ под углом φ₀ к полярной оси; координатная поверхность с уравнением r = r₀ представляет собой круговой цилиндр радиуса r₀ , осью симметрии которого является ось OZ; уравнение z = z₀ есть уравнение плоскости перпен- дикулярной оси OZ, плоходящей через её точку с координатой z₀ .

П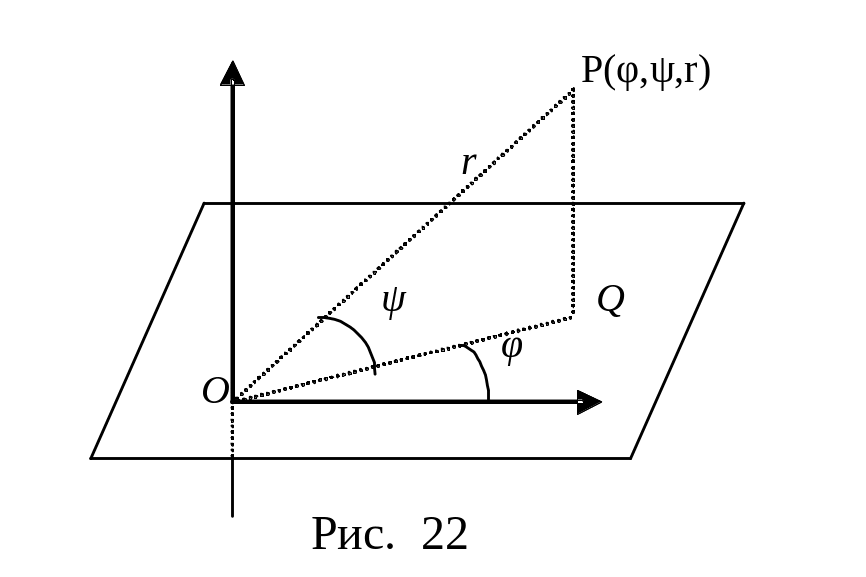 ример 3. Так же, как в примере 2 в пространстве выбрана точка О, череэ неё про- ведена плоскость и числовая ось OZ перпендикулярно плоскости. На плоскости введена полярная система координат с полюсом О. Пусть Р – произвольная точка, не лежащая на оси OZ, а Q – её проекция на плоскость. Обо- значим через φ полярный угол точки Q , через ψ – угол между отрезками ОР и О Q ; этот угол отсчитывается от О Q , его значения ле- жат в , они положительны, если Р находится в той же полуплоскости, что и поло- жительная часть оси OZ, и отрицательны в противном случае. Длину отрезка ОР обозна- чим через r. Упорядоченную тройку (φ, ψ, r) называют сферическими координатами точки Р Координатная поверхность, определяемая уравнением φ = φ₀ та же, что для цилиндрической системы - полуплоскость, проходящая через ось OZ под углом φ₀ к по- лярной оси; координатная поверхность с уравнением ψ = ψ представляет собой круго- вой конус, осью симметрии которого является числовая ось , точнее одну из половин та- кого конуса; уравнение r = r₀ есть уравнение сферы радиуса r₀ с центром в точке О .

Систему координат называют системой криволинейных координат, если хотя бы одно из семейств её координатных линий не является семейством прямых. Системы ци- линдрических и сферических координат – это системы криволинейных координат.

5.4. Преобразование координат

Пусть G – некоторое множество в , и пусть система уравнений (1) задаёт вза- имно однозначное отображение Φ множества. G на множество G*= Φ (G). В силу систе- мы (1) каждой упорядоченной тройке (х,у,z) сопоставлена упорядоченная тройка (u,v,w), где u= =U(x,y,z), v= V(x,y,z) w = W(x,y,z). В п. 5.2 тройки (x,y,z) и (u,v,w) рассмат- ривались как декартовы координаты точек Р(x,y,z) и Р*(u,v,w) . Однако, возможна и другая трактовка упорядоченной тройки (u,v,w). Поскольку каждой точке Р поставлена в со- ответствие упорядоченная тройка (u,v,w), то тем самым на множестве G введена новая система координат UVW, вообще говоря, криволинейная.; её координатные поверхности , и - это поверхности, уравнения которых в декартовой системе XYZ есть u= =U(x,y,z) , v =V (x,y,z) , w = W (x,y,z) соответственно. Таким образом, упорядоченную тройку (u,v,w) можно рассматривать и как декартовы координаты точки Р* - образа точки Р при отображении Φ, и как криволинейные координаты самой точки Р. Точка Р , декар- товы координаты которой (x,y,z), получает еще и криволинейные координаты (u,v,w), где u =U(x,y,z) , v =V (x,y,z) , w = W (x,y,z).

Итак, система уравнений (1), задающая взаимно однозначное отображение Φ мно- жества G на G*, вводит на множестве G систему криволинейных координат UVW . Ото- бражение Φ отображает точку Р с криволинейными координатами (u,v,w) в точку Р* *, для которой эта же упорядоченная тройка (u,v,w) является её декартовыми коорди- натами. Уравнения системы (1) выражают криволинейные координаты (u,v,w) точки Р через декартовы координаты (x,y,z) этой же точки; поэтому уравнения системы (1) назы- вают формулами преобразования декартовых координат точек множества G в их криво- линейные координаты. Уравнения системы (2) х = Х(u,v,w) , у =Y(u,v,w) , z = Z (u,v,w) есть формулы обратного преобразования криволинейных координат точек множества G в декартовы координаты этих же точек.

Пример 4. Пусть на плоскости ХОУ введена полярная система координат, полю- сом которой является начало декартовой системы, а полярная ось есть положительная часть оси абсцисс. Запишем формулы, выражающие декартовы координаты точки Р через её же цилиндрические координаты :

Примкр 5. Пусть - декартовы координаты точки Р, - угол между полу- плоскостью, проходящей через ось и точку Р и осью абсцисс, - угол между коорди- натной плоскостью ХОУ и отрезком ОР, а - длина этого отрезка (О – начало координат). Запишем формулы, выражающие декартовы координаты точки Р через её же сфе- рические координаты :

5.5 Замена переменных в тройном интеграле

Пусть:

G и G* - ограниченные замкнутые множества в ;

Ψ - отображение G* на G ;

- система, задающая отображение Ψ.

Теорема . (О замене переменных под знаком тройного интеграла)

Пусть отображение Ψ непрерывно на G*, непрерывно дифференцируемо на * и взаимно однозначно отображает * на , причем якобиан J_Ψ (u,v,w) не обращается в нуль на * . Если функция непрерывна на G , то

. (4)

Доказательство теоремы имеется в [1]. Теорема позволяет заменить вычисление интеграла по заданному множеству G вычислением интеграла по некоторому другому множеству G*. Обычно применение формулы (4) целесообразно, когда множество G* “ более удобно “ для интегрирования, чем множество G , например, если G* является простым относительно одной из координатных осей (см п. 5.1). Предпочтиткльнее иметь в качестве множества G* прямоугольный параллелепипед, грани которого параллельны координатным плоскостям – в таком случае все пределы интегрирования в повторном интеграле представляют собой числа. Если G* - прямоугольный параллелепипед, то гра- ница множества G состоит из координатных поверхностей системы координат, которую вводит на G отображение Ф, обратное отображению Ψ.