§ 3. Кратный интеграл

3.1. Основные определения..

Пусть Х – ограниченное измеримое множество, а функция f ограничена на Х. Обозначим через совокупность нижних интегральных сумм функции f по всевоз- можным дроблениям множества Х. Обозначим: . Из свойства 3. следует, что всякая верхняя интегральная сумма функции f является верхней гранью множества ; поэтому при любом дроблении τ справедливо ≤ τ).

Обозначим через совокупность верхних интегральных сумм функции f по все- возможным дроблениям множества Х. Число является нижней гранью этой совокупно- сти (см. выше). Обозначим: . Заметим: , так как - нижняя грань множе- ства , а - его точная нижняя грань. Таким образом, для произвольного дробления τ множества Х справедливы неравенства

τ) ≤ ≤ τ). (4)

Пусть функция f интегрируема на множестве Х, а { τ_k} - нормальная последова- тельность дроблений этого множества. Тогда при всех натуральных k справедливы нера- венства τ_k) ≤ ≤ τ_k), причем τ_k) - τ_k) . Отсюда следует, что и что I_f. , где I_f = . Кроме того, из свойства 1, п.2.4, и теоремы о “сжатой ” последовательности ([2], стр.22) вытекает равенство I_f .

Таким образом, если функция f интегрируема на ограниченном измеримом множе- стве Х , то существует число I_f такое, что для любой нормальной последовтельности { τ_k} дроблений этого множества соответствующие последовательности интегральных сумм { }, { } и { } сходятся и имеют общий предел I_f. Число I_f на- зывают интегралом ( n- кратным интегралом ) от функции f по множеству Х и обозна- чают символами и ( обозначение содержит n симво- лов ) ; множество Х называют при этом областью интегрирования, f – подынтеграль- ной функцией, – переменными интегрирования.

Итак, если f интегрируема на ограниченном измеримом множестве Х , то

, где { τ_k} - любая нормальная последовательность дроблений этого множества.

Пример 1. Пусть функция f тождественно на ограниченном измеримом множестве Х равна константе: f(х) ≡ С, С . Тогда = С .

► Функция f(х,у) ≡ С непрерывна и ограничена на Х и потому она интегрируема на этом промежутке (см. замечание к теореме 1,п.2.5). Пусть τ = - некоторое дробление множества Х, а , . Заметим: f( ) = С, , поэтому S (f, τ) = = = = C .

Пусть {τ_k} - нормальная последовательность дроблений множества Х. При всяком натуральном k имеем: S (f, τ_k) = C . Отсюда получим:

= C . ◄

Заменчание. Если функция f тождественно на множестве Х равна нулю, то = 0; если функция f тождественно на множестве Х равна единице, то равен мере множест- ва Х. Эти утверждения принято записывать так: = 0;

3.2. Свойства интеграла, выражаемые равенствами

В этом пункте Х – ограниченное измеримое множество, Х , все функции пред- полагаются интегрируемыми на Х.

1. Если мера Х равна нулю, то = 0.

► Если мера Х равна нулю, то и мера любого его подмножества X_j равна нулю; поэтому интегральная сумма функции f по любому дроблению равна нулю. Интеграл равен нулю, так как является пределом последовательности, все члены которой равны нулю. ◄

2. ( Линейное сволйство интеграла )

,где λ – число.

► Обозначим : u = f + g , v = λ f . Пусть τ = - некоторое дробление мно- жества Х. Запишем интегральные суммы по этому дроблению (здесь ξ_j- точка, выбранная в множестве ) :

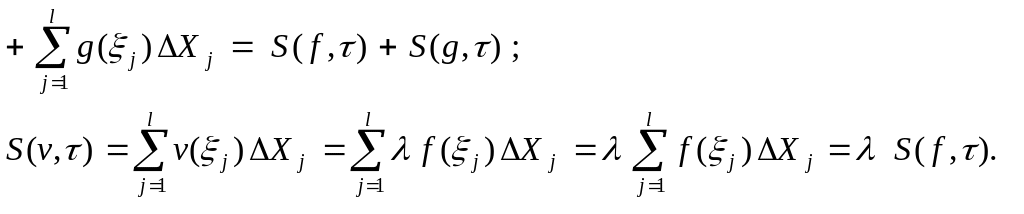(2)

Пусть - некоторая нормальная последовательность дроблений. Из (2) следует, что при всех натуральных k справедливы равенства :

(3)

Функции f и g интегрируемы по условию, функции u и v интегрируемы в силу свойств 1. и 3., п. 2.5; поэтому последовательность интегральных сумм каждой из этих функций сходится к соответствующему интегралу:

Переходя к пределу в равенствах (3), получим равенства между интегралами. ◄

3. (Аддитивность интеграла относительно области интегрирования)

Пусть множество Х разделено на два измеримых непересекающихся множества Х₁ и Х₂,: Ø. Тогда .

► Заметим, что f интегрируема на Х₁ и на Х₂ (свойство 5, п.2.5). Пусть и - нормальные последовательности дроблений Х₁ и Х₂ соответственно, и пусть при всех натуральных k τ_k = . Очевидно, есть нормальная последова- тельность дроблений множества Х, а S (f, τ_k) = S (f, τ_k ) + S (f, τ_k ) . Перейдя в этом ра- венстве к пределу, получим доказываемое равенство для интегралов. ◄

4. Пусть функция f нотрицательна и интегрируема на множестве Х . Её подграфик T_f,X является измеримым множеством, а его мера равна : = μ_n+1(T_f,X) .

► Измеримость T_f,X доказана в п. 2.5. Докажем равенство = μ_n+1(T_f,X) .

При каждом натуральном k справедливо (τ_k) T_f,X . Отсюда ( (τ_k) ) μ_n+1(T_f,X) ( ), т.е. ( см. п.1.6): μ_n+1(T_f,X) . Перейдем здесь к пределу. Так как то μ_n+1(T_f,X) = . ◄

3.3. Свойства интеграла, выражаемые неравенствами

В этом пункте Х – ограниченное измеримое множество, Х , функции f и g интегрируемы на нём.

1. Пусть функция f неотрицательна на множестве Х ; тогда интеграл от нее неот- рицателен. Если же функция f неотрицательна и непрерывна на множестве Х и , кроме того, существует внутренняя точка множества Х , в которой функция принимает положи- тельное значение, то интеграл строго больше нуля.

► Интегральные суммы неотрицательной функции неотрицательны; значит, неот- рицательным будет и как предел последовательности неотрицательных чисел.

Докажем второе утверждение. Пусть x₀ есть внутренняя точка множества Х, и пусть f(x₀) > 0. Так как , по теореме о стабилизации знака непрерывной функции ([3], стр.14) найдется ε > 0 такое, что при всех выполняется f(x) >½ f(x₀). Значит, цилиндр С, основанием которого является круг , а высота равна ½ f(x₀), целиком содержится в подграфике , Отсюда: = μ_n+1(T_f,X) ≥ 0 . ◄

2. Пусть на множестве Х . Тогда .

► Положим h = g – f . Функция h неотрицательна на Х и интегрируема на нем ( свойства 1. и 3., п. 2.5). Значит, 0. В силу линейного свойства интеграла = ≥ 0. Отсюда: . ◄

3. .

► Если f интегрируема, то и | f | - интегрируемая функция (п.2.5.). При всяком имеем: . Отсюда и из свойства 3 : , а это равносильно доказываемому неравенству. ◄

3.4. Теоремы о среднем для n- кратных интегралов

Теорема 1. Пусть Х – ограниченное измеримое множество, а функции f и g интегрируемы на нем, причем g не меняет знак на Х. Обозначим :

. Тогда существует μ, m ≤ μ ≤ M. такое, что ,

► Будем считать g неотрицательной функцией. При имеем : m ≤ f(х) ≤ M. Умножим эти неравенства на неотрицательный множитель g(х): m g(х) ≤ f(х) g(х) ≤ M g(х). По свойству 2 предыдущего пункта:

(4) Так как g неотрицательна, возможны два случая: *) и **)

*) Из (4) в этом случае следует, что и Значит, доказываемое равенство справедливо при любом μ , в том числе при любом μ, m ≤ μ ≤ M.

**) Положим. Очевидно, при таком μ доказываемое равенство спра- ведливо, а из (4) имеем : m ≤ ≤ M , т.е. m ≤ μ ≤ M.

Т. о., число μ, удовлетворяющее указанным в теореме требованиям, существует всегда.◄

Теорема 2. Пусть функция f непрерывна на замкнутом ограниченном множестве Х , а функция g интегрируема на Х и не меняет на этом множестве знак. Тогда суще- ствует точка такая, что

► Функция f интегрируема на Х ( теорема1, п. 2.5). Следовательно, выполнены все требования условия предыдущей теоремы ; поэтому справедливо и ее утверждение: существует μ, m ≤ μ ≤ M, такое, что имеет место равенство . По теореме Вейерштрасса ([3], стр.15) функция f достигает на множестве Х своих точных граней, т.е., в множестве Х существуют точки и такие, что f( ) = m, f( ) = M. Т.о., число μ лежит между двумя значениями функции: f( ) ≤ μ ≤ f( ). По теореме Коши о промежуточном значении ([3], стр.15) существует точка такая, что f( ) = μ. Подставив это значение μ в , получим доказываемое равенство. ◄

п.3.5. Сечение множества. Проекция множества на координатную ось.

Пусть Х - некоторое множество, ξ- некоторое вещественное число. Обозна- чим: . является совокупностью тех точек множест- ва Х , первая координата х₁ которых равна ξ.. Эту совокупность назовём сечением множе- ства Х. Заметим, что при некоторых ξ сечение может оказаться пустым множеством Р Λ – тогда, когда в Х нет точек вида . Множество тех чисел ξ, при которых се- чение не пусто, назовём проекцией множества Х на координатную ось х₁ и обозна- чим через : .

ис. 5 а) иллюстрирует введённые выше понятия для случая n = 2. На нём множество Х представлено плоской фигурой, сечение - отрезком прямой х=ξ, лежащим внутри Х, проекция - отрезком оси абсцисс.

Аналогично сечению введём сечения , ,…, и проекции множества Х на соответствующие координатные оси. Например,

, . На рис. b) изображено сечение множества Х и его про- екция на ось ординат.

Пусть Х , и пусть при каждом ξ, принадлежащем проекции Х на одну из ко-ординатных осей х_i, соответствующее сечение измеримо. В таком случае на про- екции можно определить функцию σ_i(ξ) равенством σ_i(ξ) = .

Теорема . ( Об отыскании меры множества по его сечениям)

Пусть Х - ограниченное измеримое множество, и пусть выполнены следу- ющие условия:

1. проекция множества Х на координатную ось х_i представляет собой ограниченный промежуток ;

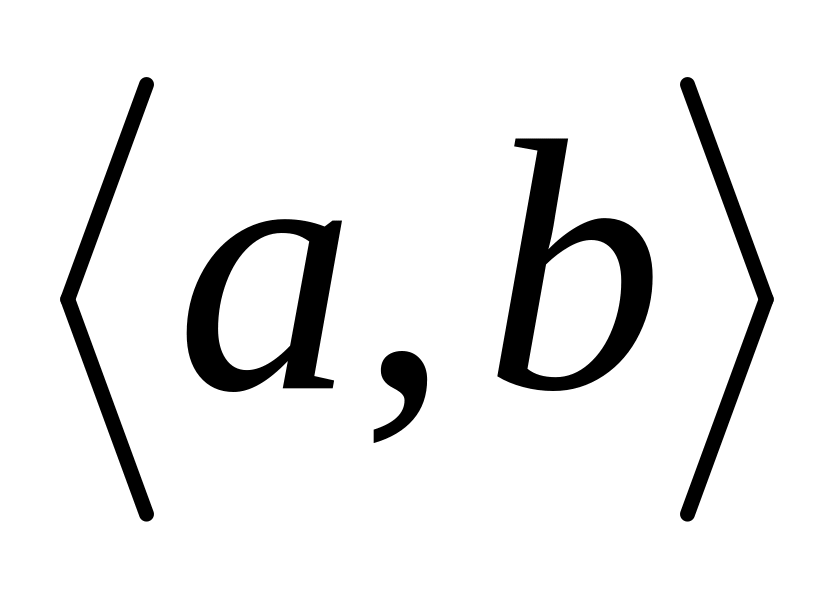2. при каждом ξ, принадлежащем , сечение измеримо;

3) функция σ_i(ξ) = интегрируема на .

Тогда .

Доксзательство теоремы не приводим, его можно найти в руководствах по мате- матическому анализу . (Булдырев, Павлов).