
Министерство образования Российской Федерации
----------
САНКТ- ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
И.Ю. РЫЖАКОВ
Кратные интегралы
Учебное пособие
Санкт-Петербург
Издательство СПбГПУ
2011
УДК 5172
Р ы ж а к о в И. Ю.Кратные интегралы Учебное пособие. СПб.: Изд- во СПбГПУ, 2011. 45 стр.
Пособие соответствует гоcударственному стандарту дисциплины “ Математика “ направлений бакалаврской подготовки 553100 ‹‹Техническая физика›› и550700 ‹‹Электроника и микроэлектроника››
Содержит изложение теоретического материала в соответствии с действующей программой по теме ‹‹Введение в анализ›› , большое количество разобранных примеров, а также упражнений.
Предназначено студентам первого курса радиофизического факультета.
Ил. 8. Библиогр : 2 назв.
Печатается по решению редакционно- издательского совета Санкт-Петербургского государственного политехнического университета.
© Санкт-Петербургский государственный
политехнический университет, 2010
© Рыжаков И.Ю., 2011
§ 1. Мера в пространстве .
![]()
1.1.
Клетка в
пространстве
![]() и
её обьём.
и
её обьём.
Пусть
![]() ,
,
![]() ,
i
= 1,2,…,
n
– некоторые
промежутки; они могут быть любы- ми -
открытыми, замкнутыми или полуоткрытыми,
ограниченными или неограниченны- ми).
Обозначим через К
совокупность
тех точек х
(х1,
х2,
… , х n)
,
i
= 1,2,…,
n
– некоторые
промежутки; они могут быть любы- ми -
открытыми, замкнутыми или полуоткрытыми,
ограниченными или неограниченны- ми).
Обозначим через К
совокупность
тех точек х
(х1,
х2,
… , х n)![]() ,
координаты кото- рых удовлетворяют
условиям : xi
,
i
= 1,2,…,
n:
,
координаты кото- рых удовлетворяют
условиям : xi
,
i
= 1,2,…,
n:

![]() ,
i = 1,2,…, n
,
i = 1,2,…, n![]() .
Множество
К называют
n
– мерным
промежутком, а также брусом или клеткой
в прост- ранстве
;
длины промежутков
,
i = 1,2,…,
n
называют
измерениями
клетки К.
На рис. 1 представлены
геометрические интерпретации клетки
К в
при
n
= 1,2,3 - проме-
-жуток числовой оси, прямоугольник,
прямоугольный параллелепипед
соответственно.
.
Множество
К называют
n
– мерным
промежутком, а также брусом или клеткой
в прост- ранстве
;
длины промежутков
,
i = 1,2,…,
n
называют
измерениями
клетки К.
На рис. 1 представлены
геометрические интерпретации клетки
К в
при
n
= 1,2,3 - проме-
-жуток числовой оси, прямоугольник,
прямоугольный параллелепипед
соответственно.
Если хотя бы один из промежутков , i = 1,2,…, n является пустым множе- ством ( пустым множеством является интервал (a; a), где a – некоторое число ), то и клет- ка К – пустое множество. Если все промежутки , i = 1,2,…, n ограничены, то и К – ограниченное множество в ; если же хотя бы один из этих промежутков неограничен, то К - неограниченное множество в .
Если все промежутки , i = 1,2,…, n представляют собой интервалы, то клетка К –открытое множество, т.е. граница К не принадлежит К. Если все , i = =1,2,…, n являются сегментами, замкнутыми промежутками, то и К - замкнутое множе- ство, граница К принадлежит К.
Введем понятие об обьёме (n – мерном обьёме) клетки К . Эту величину обозначим символом υK и определим её так:
если среди промежутков , i = 1, 2,…, n , имеется хотя бы один, длина которого равна нулю, то υK = 0;
если длины всех промежутков , i = 1, 2,…, n больше нуля, причём среди них имеется хотя бы один неограниченный промежуток, то υK =
 ;
;
если все , i = 1,2,…, n – ограниченные промежутки положительной длины, то υK
 ;
т.е., в этом случае обьём клетки равен
произведе- нию её измерений.
;
т.е., в этом случае обьём клетки равен
произведе- нию её измерений.
При
n
= 1 К
есть промежуток
![]() , а υK
=
, а υK
=
![]() - длина этого промежутка; при n=2
К
представдяет собою прямоугольник:
- длина этого промежутка; при n=2
К
представдяет собою прямоугольник:
![]() ,
а υK
=
,
а υK
=
![]() есть его площадь; при
n
= 3
есть его площадь; при
n
= 3
![]()
![]() - прямоугольный параллелепипед, а
υK
=
- прямоугольный параллелепипед, а
υK
=![]() - его обьём, см. рис. 1.
- его обьём, см. рис. 1.
Итак,
для всякой клетки К,
К
,
имеем: 0 ≤ υK
≤ + ∞, причём
возможен и случай υK
= 0, и случай υK
=![]() .
Отметим ещё, что υK
не зависит от того, промежутками какого
типа (открытыми, замкнутыми, полуоткрытыми)
являются
,
i
= 1,2,…,
n.
.
Отметим ещё, что υK
не зависит от того, промежутками какого
типа (открытыми, замкнутыми, полуоткрытыми)
являются
,
i
= 1,2,…,
n.
1.2. Верхняя мера множества.
Пусть
Х , Х![]() ,-
некоторое множество, и пусть
,-
некоторое множество, и пусть
![]() ,
Хi
,-
некоторая ко -нечная или счётная
последовательность (система) множеств
( т.е. s
– либо
натуральное число, либо
).
Систему
назовём покрытием
множества
Х, если
,
Хi
,-
некоторая ко -нечная или счётная
последовательность (система) множеств
( т.е. s
– либо
натуральное число, либо
).
Систему
назовём покрытием
множества
Х, если
![]() ,
т.е., если каждая точка множества Х
принадлежит
хотя бы одному из множеств Хi
, i
= =1,2,…, s.
,
т.е., если каждая точка множества Х
принадлежит
хотя бы одному из множеств Хi
, i
= =1,2,…, s.
Пусть
Х, Х
,
- некоторое множество, и пусть РХ
=![]() ,
Кi
,
- покрытие множества Х
, состоящее
из конечного или счётного количества
клеток. Обозначим:
,
Кi
,
- покрытие множества Х
, состоящее
из конечного или счётного количества
клеток. Обозначим:
![]() .
Если в покрытии РХ
=
имеется хотя
бы одна клетка, обьём которой равен
,
то и
.
Если в покрытии РХ
=
имеется хотя
бы одна клетка, обьём которой равен
,
то и
![]() =
.
Если же обьёмы всех клеток, составляющих
прокрытие РХ
,
меньше
,
то
=
.
Если же обьёмы всех клеток, составляющих
прокрытие РХ
,
меньше
,
то
![]() представляет собой либо сумму конечного
количества неотрица- тельных чисел
(если s
N
), либо
числовой ряд с неотрицательными членами
(если s
= =
).
Такой ряд может оказаться сходящимся
или расходящимся; в первом случае его
сумма есть неотрицательное число, во
втором она равна
.
представляет собой либо сумму конечного
количества неотрица- тельных чисел
(если s
N
), либо
числовой ряд с неотрицательными членами
(если s
= =
).
Такой ряд может оказаться сходящимся
или расходящимся; в первом случае его
сумма есть неотрицательное число, во
втором она равна
.
Порядок, в котором занумерованы клетки, образующие покрытие РХ = , мо- жет быть изменен. Его изменение приводит к перестановке слагаемых в сумме . Напомним, что перестановка членов ряда с неотрицательными членами не влияет на его сумму; следовательно, в любом случае величина не зависит от того, в каком порядке занумерованы клетки, образующие покрытие РХ .
Заданное
множество Х
может быть
покрыто различными системами клеток.
Обо- значим через![]() совокупность всевозможных покрытий
множества Х
конечными или счётными системи клеток.
Всякому
покрытию РХ
, принадлежащему
совокупности
,
соответствует величина
- это либо некоторое неотрицательное
число, либо
.
Точную нижнюю грань величин
на совокупности
всевозможных
покрытий множества Х
конечными или счётными системи клеток,
назовём верхней
мерой множест- ва Х
и обозначим через
совокупность всевозможных покрытий
множества Х
конечными или счётными системи клеток.
Всякому
покрытию РХ
, принадлежащему
совокупности
,
соответствует величина
- это либо некоторое неотрицательное
число, либо
.
Точную нижнюю грань величин
на совокупности
всевозможных
покрытий множества Х
конечными или счётными системи клеток,
назовём верхней
мерой множест- ва Х
и обозначим через
![]() :
:
![]()
![]()
Так
как
≥
0 для любого РХ
, то![]() ,
причём возможны оба крайних значения
=
0 ( например, если Х
содержит
только одну точку) и
=
(
например, если Х
=
)
.
,
причём возможны оба крайних значения
=
0 ( например, если Х
содержит
только одну точку) и
=
(
например, если Х
=
)
.
Пусть
![]() ;
тогда
;
тогда
![]() .
Действительно, всякое покрытие множества
Х2
является
также и покрытием множества Х1;
значит,
.
Действительно, всякое покрытие множества
Х2
является
также и покрытием множества Х1;
значит,
![]() .
.
Можно
доказать, что для любых непересекающихся
множеств Х1
и
Х2
справедливо
неравенство
![]()
![]() ,
причём здесь возможен и случай равенства
,
причём здесь возможен и случай равенства
![]() ,
и случай строгого неравенства
,
и случай строгого неравенства
![]() .
.
С целью устранить из дальнейших рассмотрений множества, для которых имеет место записанное выше строгое неравенство, введем понятие об измеримых множествах.
1.3 Измеримые множества
Пусть
Х , Х
,=
некоторое множество. Введём обозначение:
![]()
 .
Множество
.
Множество
![]() называют дополнением множества Х.
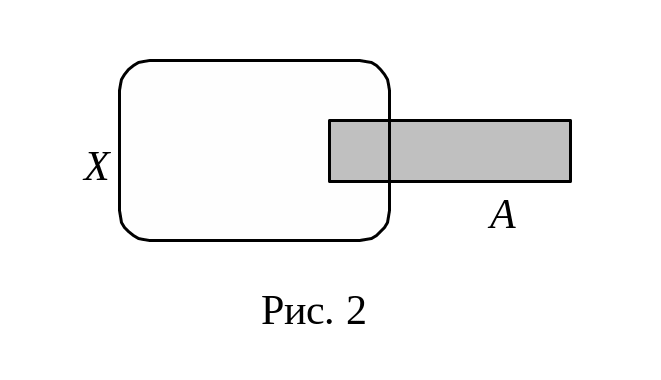
Всякое непустое множество А
можно представить как обьединение двух
непе- ресекающихся множеств - пересечения
А с
Х и
пересе- чения А
с дополнением
(см. рис. 2.):
называют дополнением множества Х.
Всякое непустое множество А
можно представить как обьединение двух
непе- ресекающихся множеств - пересечения
А с
Х и
пересе- чения А
с дополнением
(см. рис. 2.):
![]() (
пересечение
(
пересечение![]() или
или
![]() может
оказаться пустым множеством)
. В силу
отмечен- меченного в п.2 свойства верхней
меры для любого
множества
А
справедливо:
может
оказаться пустым множеством)
. В силу
отмечен- меченного в п.2 свойства верхней
меры для любого
множества
А
справедливо:
![]() .
.
Определение. Множество Х , Х , назовем измеримым, если для всякого А, А , имеет место равенство
![]() .
.
Справедливы следующие утверждения.
Всякая клетка К есть измеримое множество.
Всякое открытое множество Х измеримо.
Всякое замкнутое множество Х измеримо.
Если верхняя мера множества Х равна нулю, то множество Х измеримо.
Если верхняя мера границы
 множества
Х
равна
нулю, то множество Х
измеримо.
множества
Х
равна
нулю, то множество Х
измеримо.
Обозначим совокупность всевозможных измеримых множеств в через L n . Ввиду утверждений 1.- 5. понятно, что L n - весьма широкая совокупность, ведь ей при- надлежат любые открытые и любые замкнутые множества , и не только они. Практически всякое множество, с которым приходится иметь дело в прикладных областях математики измеримо. Множества, не входящие в L n , существуют, однако все они обладают столь сложной структурой, что мы уклонимся от построения какого–нибудь конкретного приме- ра неизмеримого множества из-за громоздкости такого построения. Примеры неизмери- мых множеств можно найти в руководствах по математическому анализу.
Добавим к утверждениям 1. – 5. свойства основных операций над измеримыми множествами.
6. Обьединение конечного или счётного количества измеримых множеств есть измеримое множество.
7. Пересечение конечного или счётного количества измеримых множеств есть измеримое множество.
Разность двух измеримых множеств есть измеримое множество.
Доказательства утверждений 1. – 8. можно найти в руководствах по математиче- скому анализу, см., например, [2] .
1.4. Монотонные последовательности множеств.
Пусть
![]() -
некоторая бесконечная последовательность
множеств в
.
-
некоторая бесконечная последовательность
множеств в
.
Определение.
Последовательность
назовём
возрастающей (убывающей)
, если при всяком натуральном k
выполняется
условие
![]() .
.
Возрастающие и убывающие последовательности называют монотонными после- довательностями.
Пусть
- возрастающая последовательность.
Обозначим:
![]() .
Множе- ство Х
будем называть
пределом
возрастающей последовательности
и будем за- писывать:
.
Множе- ство Х
будем называть
пределом
возрастающей последовательности
и будем за- писывать:
![]() .
Заметим: для всякой точки х0,
принадлежащей Х,
существует
натура- льное k0
такое, что при всех k
>
k0
выполняется
х0
.
Заметим: для всякой точки х0,
принадлежащей Х,
существует
натура- льное k0
такое, что при всех k
>
k0
выполняется
х0![]() .
.
Пусть
-убывающая последовательность. Обозначим:
![]() .
Множе- ство Х
будем называть
пределом
убывающей последовательности
и будем запи- сывать:
.
Множе- ство Х
будем называть
пределом
убывающей последовательности
и будем запи- сывать:
![]() .
Всякая точка множества Х
принадлежит
каждому из множеств
.
Всякая точка множества Х
принадлежит
каждому из множеств![]() ,
k
= 1,2, … ..
,
k
= 1,2, … ..
Пример.
Обозначим:![]() ,
,
![]() .
Последовательность замкнутых кругов
.
Последовательность замкнутых кругов
![]() -
возрастающая, её пределом является отк-
рытый круг
-
возрастающая, её пределом является отк-
рытый круг![]() .
Последовательность открытых кругов
.
Последовательность открытых кругов![]() -
убы- ващая, её пределом является замкнутый
круг
-
убы- ващая, её пределом является замкнутый
круг
![]() .
.
Из отмеченных в предыдущем пункте свойств операций над измеримыми множе- ствами следует, что предел монотонной последовательности измеримых множеств явля- ется измеримым множеством.
1.5. Мера измеримого множества.
Определение. Мерой ( n –мерной мерой ) измеримого множества Х L n называют его верхнюю меру.
Обозначать
n
–мерную
меру измеримого множества Х
будем символом
![]() .
Таким образом, если
.
Таким образом, если
![]() ,
то
,
то
![]() .
.
Справедливы следующие утверждения о свойствах меры измеримого множества.
.( неотрицательность ). Мера всякого неотрицательна, причём возможен и случай = 0, и случай = .
.(полная аддитивность). Пусть , Хi , - конечная или счётная система попарно непересекающихся измеримых множеств; тогда
![]() .
.
.( инвариантность). Если измеримые Х1 и Х2 конгруентны, то
 .
.
Замечание 1. Два множества, лежащие в , называют конгруентными, если су- ществует движение пространства ( т.е. преобразование , не меняющее расстояния меж- ду его точками), отображающее одно из этих множеств на другое.
4..(нормированность). n- мерная мера клетки К равна её n – мерному обьёму:
![]() =
υK.
Доказательства этих утверждений можно
найти, например, в [1].
=
υK.
Доказательства этих утверждений можно
найти, например, в [1].
Замечание
2.
В силу
сформулированного определения каждому
множеству Х
Ln
поставлено в соответствие число – его
мера
:
![]()
![]()
![]() .
Тем самым на совокупности измеримых
множеств Ln
задана функция, которую естественно
обозначить через
.
Тем самым на совокупности измеримых
множеств Ln
задана функция, которую естественно
обозначить через
![]() .
Эту функцию называют мерой ( n
–мерной
мерой Лебега) . Можно доказать, что среди
всевозможных функций, заданных на
совокупности Ln
, только
обладает
полным набором свойств 1) – 4) -
неотрицательностью, полной аддитивностью,
инвариантностью, нормированностью.
.
Эту функцию называют мерой ( n
–мерной
мерой Лебега) . Можно доказать, что среди
всевозможных функций, заданных на
совокупности Ln
, только
обладает
полным набором свойств 1) – 4) -
неотрицательностью, полной аддитивностью,
инвариантностью, нормированностью.
Сформулированные ниже утверждения 5) – 8) являются следствиями свойств 1) – - 4).
5.(монотонность).
Если Х1
и Х2
измеримы и Х1
Х2
, то
![]() .
.
6..(субаддитивность). Пусть , - конечная или счётная система измеримых множеств; тогда
а)
![]() ;
;
b)
если при всех k
≠ j
![]() ,
то
.
,
то
.
Замечание 3. Равенство справедливо не только тогда, когда множества Xi ,i= 1,2,…,s попарно не пересекаются; оно справедливо и в случае, когда по- парные пересечения хотя и не пусты, но мера каждого из них равна нулю .
7.(непрерывность
меры снизу).
Пусть
-
возрастающая последовательность
измеримых множеств, и пусть
![]() .
Тогда
.
Тогда
![]() .
.
8.(непрерывность меры сверху). Пусть - убывающая последовательность измеримых множеств, и пусть . Тогда .
Определение.
Множество
Х
назовём
множеством меры нуль,
если его верхняя мера равна нулю:
![]() =
0.
=
0.
Замечание
4.
Всякое
множество Х
меры нуль
измеримо, а его мера равна нулю:
![]() .
Всякое подмножество множества меры
нуль есть множество меры нуль.
.
Всякое подмножество множества меры
нуль есть множество меры нуль.
► Пусть
Х –
множество меры нуль. Его измеримость
вытекает непосредственно из утверждения
4, п. 1.3., а равенство
следует из определения меры
![]()
Пусть
Х –
множество меры нуль, а Y
– его
подмножество:
Y
X.
По свойству
верхней меры
![]()
![]() ;
значит,
;
значит,
![]() .◄
.◄
Двумерная
мера
![]() простейших плоских фигур – треугольника,
параллелограм- ма, трапеции, вообще
любой многоугольной фигуры, а также
круга, эллипса – есть пло- щадь этих
фигур. В дальнейшем функцию
мы будем наэывать площадью, а величину
простейших плоских фигур – треугольника,
параллелограм- ма, трапеции, вообще
любой многоугольной фигуры, а также
круга, эллипса – есть пло- щадь этих
фигур. В дальнейшем функцию
мы будем наэывать площадью, а величину
![]() ,
где
,
где
![]() ,
- площадью плоской измеримой фигуры Х.
,
- площадью плоской измеримой фигуры Х.
Трёхмерная
мера
![]() простейших
геометрических тел – призмы, пирамиды,
вообще любого многогранника, а также
шара, эллипсоида – равна обьёму этих
тел. В дальнейшем функцию
мы будем называть обьёмом (трёхмерным
обьёмом), а величину
простейших
геометрических тел – призмы, пирамиды,
вообще любого многогранника, а также
шара, эллипсоида – равна обьёму этих
тел. В дальнейшем функцию
мы будем называть обьёмом (трёхмерным
обьёмом), а величину
![]() ,
где
,
где
![]() ,
- обьёмом трёхмерного измеримого
множества (тела ) Х.
,
- обьёмом трёхмерного измеримого
множества (тела ) Х.
1.6. Цилиндрические множества в
Пусть Х - некоторое множество, а .h1 и h2 - заданные числа, h1 ≤ h2 . Обозначим:
![]()
![]()
![]()
Множество
С назовем
цилиндром,
число h
= h2
–h1
высотой
цилиндра С, множе-
ства![]() и
и
![]() -
нижним и верхним основаниями цилиндра
С соответственно.
На рис. 3 горизонтальная координатная
плоскость изображает пространство
.
-
нижним и верхним основаниями цилиндра
С соответственно.
На рис. 3 горизонтальная координатная
плоскость изображает пространство
.
Т еорема
. Пусть
Х
-
измеримое множество. Тогда :
еорема
. Пусть
Х
-
измеримое множество. Тогда :
1) цилиндр С – измеримое множество;
2)
![]()
Доказательства этих утверждений мож- но найти в руководствах по математическому анализу.
