Относительное положение прямой и плоскости, двух плоскостей

1. Прямая и плоскость могут быть: параллельными и пересекаться.

Признак параллельности прямой плоскости: Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей плоскости.

2. Плоскости в пространстве могут быть параллельными или пересекаться.

3. Признаком параллельности плоскостей общего положения является параллель­ность двух пересекающихся прямых одной плоскости соответственно двум пересекаю­щимся прямым другой плоскости. Признаком параллельности плоскостей частного по­ложения является параллельность их одноимённых следов-проекций.

4. У параллельных плоскостей одноимённые линии уровня параллельны.

Построение точки пересечения прямой и плоскости, а так же линии пересечения плоскостей рассматриваются в разделе главные позиционные задачи.

Перпендикулярность прямой и плоскости, двух плоскостей

Теорема об ортогональных проекциях прямых углов: Если одна сторона прямого угла параллельна плоскости проекций (является прямой уровня – горизонталью или фронталью), то на эту плоскость прямой угол проецируется без искажений (рис. 23).

Нормаль к проецирующей плоскости на чертеже является прямой уровня и одна из её проекций перпендикулярна к вырожденной проекции плоскости (рис. 24).

Нормаль к плоскости общего положения. На комплексном чертеже её горизонтальная и фронтальная проекции соответственно перпендикулярны к натуральным проекциям горизонтали и фронтали этой плоскости (рис. 25).

Если плоскость проходит через перпендикуляр к другой плоскости, то такие плоскости взаимно перпендикулярны.

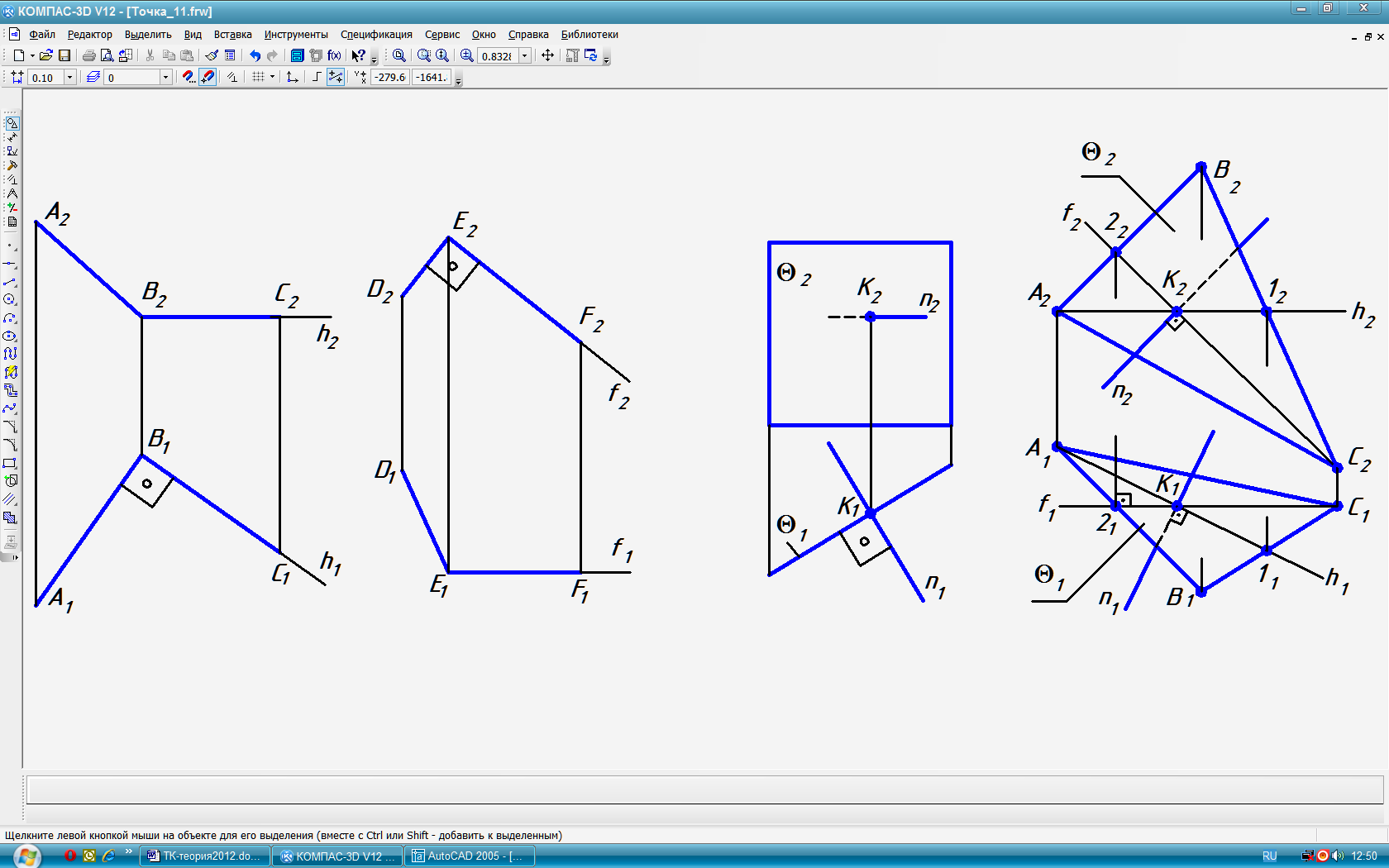
Рис. 23 Рис. 24 Рис. 25

Многогранники и тела вращения

Многогранником называется тело, ограниченное со всех сторон плоскостями. Элементы многогранника: грани, рёбра, вершины. Совокупность всех рёбер многогранника называется его сеткой. Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани; при этом его грани являются выпуклыми многоугольниками. Для выпуклых многогранников Леонардом Эйлером предложена формула:

Г+В-Р=2, где Г-число граней; В – число вершин; Р – число рёбер.

Среди множества выпуклых многогранников наибольший интерес представляют правильные многогранники (тела Платона), пирамиды и призмы. Многогранник называется правильным, если все его грани являются равными правильными многоугольниками. К ним относятся (рис. 26): а - тетраэдр; б - гексаэдр (куб); в - октаэдр; г - додекаэдр; д - икосаэдр.

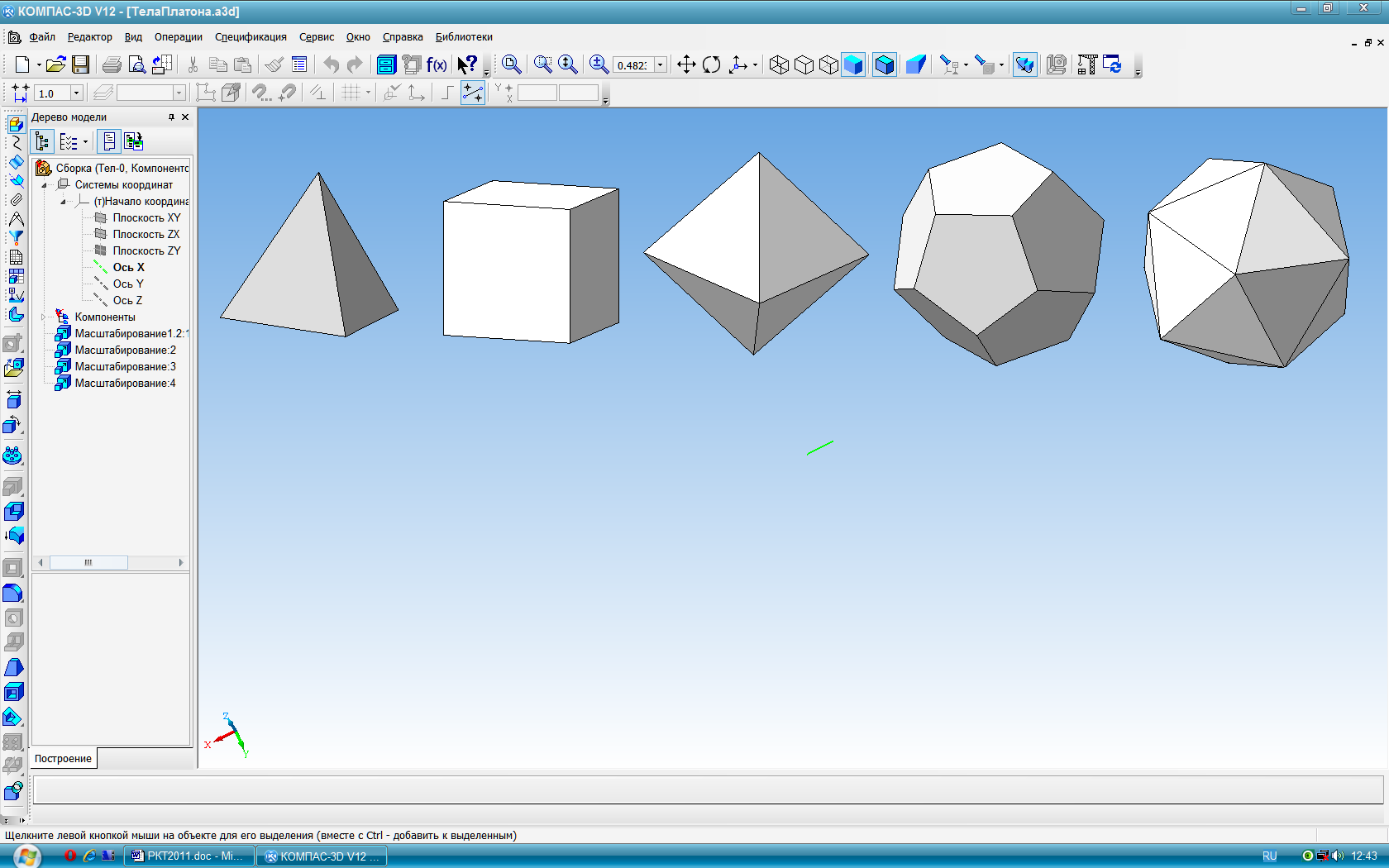
а) б) в) г) д)

Рис. 26

Параметры правильных многогранников (рис. 26)

Правильный многогранник (тело Платона)		Число								Угол между смежными рёбрами, град.
		граней		вершин		рёбер		сторон у каждой грани				Число рёбер у каждой вершины
Тетраэдр	4		4		6		3		60		3
Гексаэдр (куб)	6		8		12		4		90		3
Октаэдр	8		6		12		3		60		4
Додекаэдр	12		20		30		5		72		3
Икосаэдр	20		12		30		3		60		5

Из таблицы видно, что число граней и вершин у куба и октаэдра соответственно составляет 6, 8 и 8, 6. Это позволяет вписывать (описывать) их в друг друга до бесконечности (рис. 27).

Большую группу составляют, так называемые, полуправильные многогранники (тела Архимеда). Это выпуклые многогранники, у которых грани являются правильными многоугольниками разных типов. Тела Архимеда это усечённые тела Платона. Внешний вид некоторых из них представлены на рис. 28, а ниже их параметры в таблице.

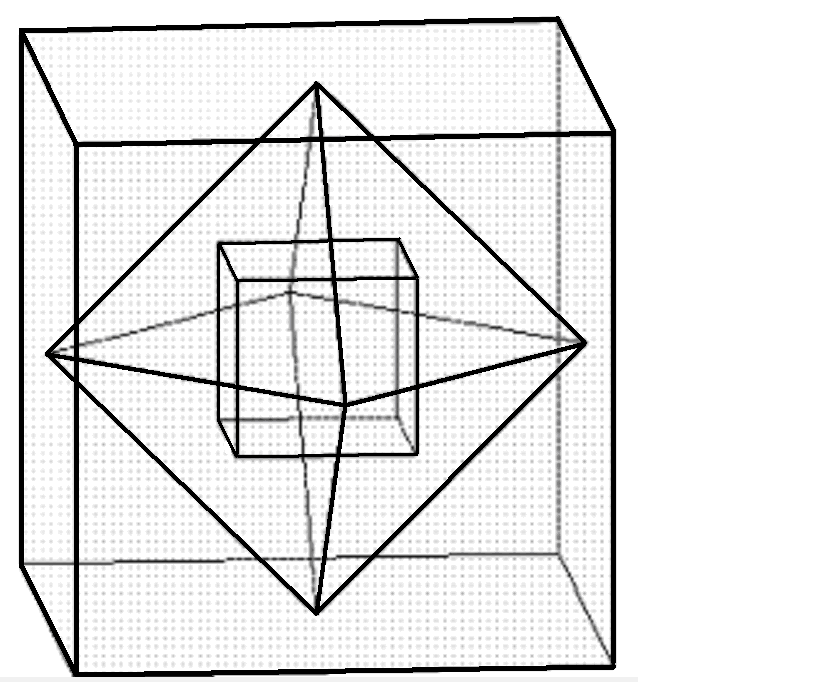
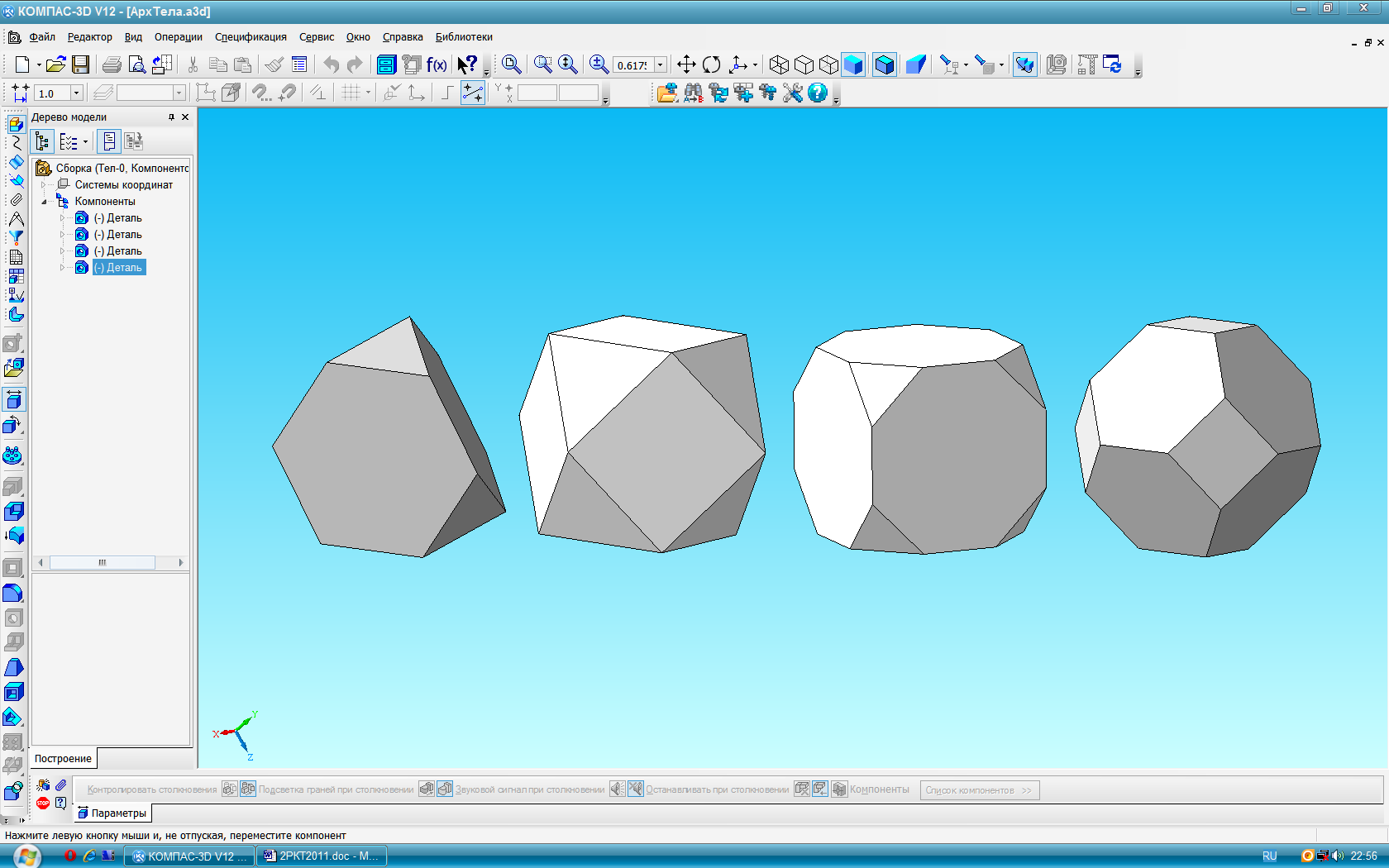
а) б) в) г)

Рис. 27 Рис. 28

Параметры полуправильных многогранников (рис. 28)

Обознач. (рис. 20)	Полуправильные многогранники (тела Архимеда)	Число вершин	Число рёбер	Число граней	Состав граней
а	Усечённый тетраэдр	12	18	8	4-треугольника + 4-шестиугольника
б	Кубооктаэдр	12	24	14	8-теугольников + 6-квадратов
в	Усечённый куб	24	36	14	8-треугольников + 6-восмиугольников
г	Усечённый октаэдр	24	36	14	6-квадратов + 8-шестиугольников

Многогранник может занимать общее положение в пространстве, или же его элементы могут быть параллельными и (или) перпендикулярными к плоскостям проекций. Исходными данными для построения многогранника в первом случае служат координаты вершин, во втором ─ его размеры. Построение проекций многогранника сводится к построению проекций его сетки. Наружный очерк проекции многогранника называют контуром тела.

Призма

─ выпуклый многогранник, боковые рёбра которого параллельны между собой. Нижняя и верхняя грани ─ равные многоугольники, определяющие количество боковых рёбер, называются основаниями призмы. Призма называется правильной, если в основании правильный многоугольник, и прямой, если боковые рёбра перпендикулярны к основанию. В противном случае призма наклонная. Боковые грани прямой призмы прямоугольники, а наклонной ─ параллелограммы. Боковая поверхность прямой призмы относится к проецирующим объектам и вырождается в многоугольник на перпендикулярную боковым рёбрам плоскость проекций. Проекции точек и линий, расположенных на боковой поверхности призмы, совпадают с её вырожденной проекцией.

Типовая задача 3 (рис. 29): Построить комплексный чертёж прямой призмы с размерами: l- сторона основания (длина призмы); b- высота равнобедренного треугольника основания (ширина призмы); h- высота призмы. Определить положение рёбер и граней относительно плоскостей проекций. На гранях ABB’A’ и ACC’A’ задать фронтальные проекции соответственно точки M и прямой n и построить их недостающие проекции.

1. Мысленно располагаем многогранник в системе плоскостей проекций так, чтобы его основание ABC║₁ ;а ребро АС║₃ (рис. 29, а).

2. Мысленно вводим базовые плоскости: ║₁ и совпадающую с основанием (ABC); ║₂ и совпадающую с задней гранью АСС’А’. Строим базовые линии ____ (рис. 29, б).

3. Строим горизонтальную, затем фронтальную и, наконец, профильную проекции призмы, используя базовые линии __ (рис. 29, в).

4. Анализируем положение рёбер и граней на комплексном чертеже пирамиды, учитывая исходные данные и классификаторы положения прямых и плоскостей (с. 11,14).

Рёбра: АВ, ВС ─ горизонтали; АС ─ профильно-проецирующая; AS, SC, SB ─ горизонтально-проецирующие. Грани: ABC A'B’C’ ─ горизонтальные уровня; ABВ’А’, BCС’В’ ─ горизонтально-проецирующие; ACC'А’ ─фронтальная уровня..

5. Построение горизонтальных проекций точек, лежащих на боковых гранях призмы, выполняем с использованием собирательного свойства проецирующего объекта: все проекции точек и линий, расположенных на боковой поверхности призмы, совпадают с её вырожденной (горизонтальной) проекцией. Профильные проекции точек (например М) строим откладывая по горизонтальным линиям связи их глубины (Y_M ) от _ , которые измеряются на горизонтальной проекции от ₁ (см. также с. 8, 17). На прямой n задаём точки 1, 2 и строим эти точки на поверхности призмы, аналогично точке М. Определяем видимость методом конкурирующих точек. Выполнение задания "Призма с вырезом" см. в [14].

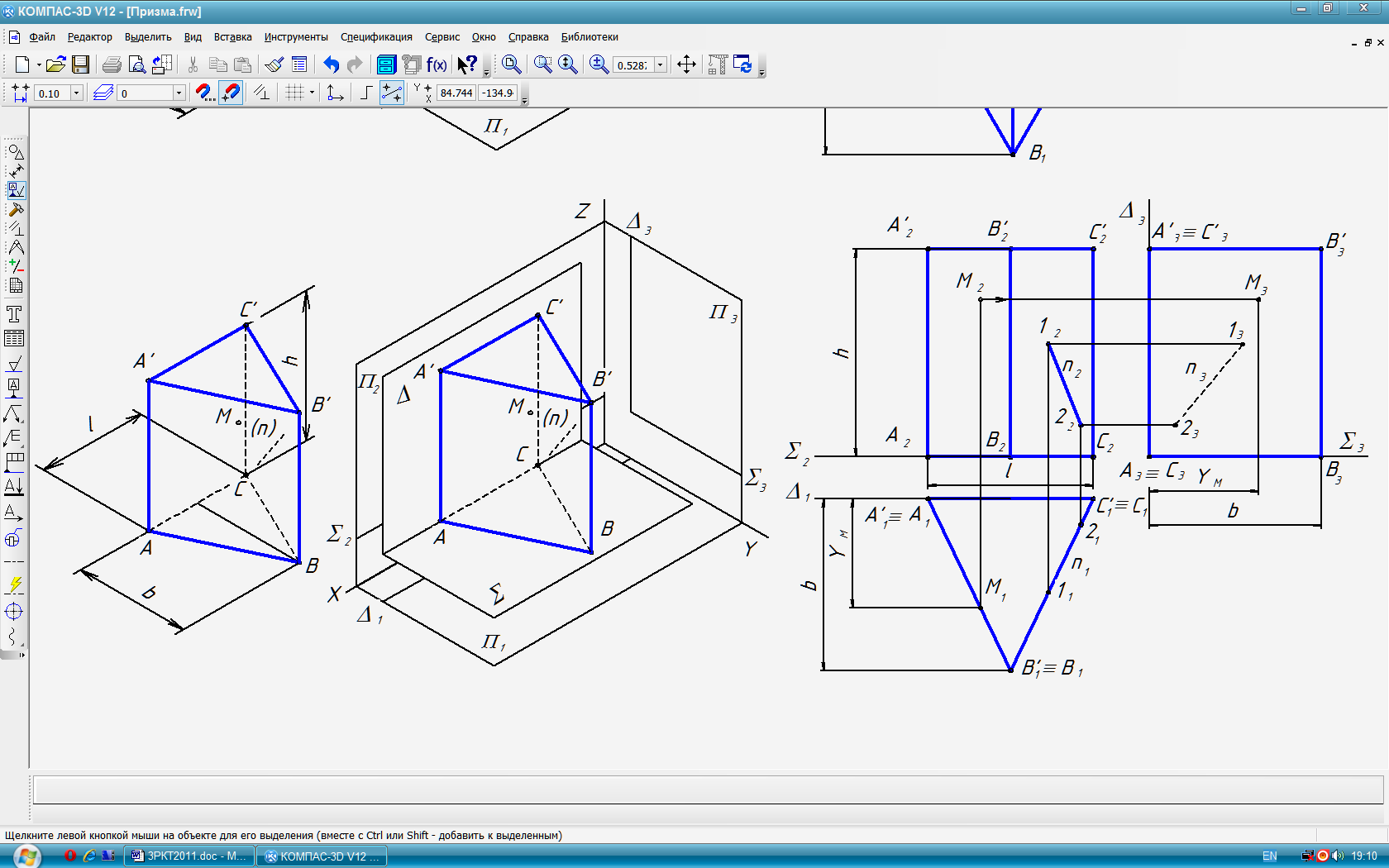
а) б) в)

Рис. 29