
- •Руководство к выполнению упражнений и заданий по начертательной геометрии
- •Ростов-на-дону
- •Введение
- •Литература
- •Основы начертательной геометрии
- •Основоположник начертательной геометрии
- •Основные понятия
- •Символы математической логики:
- •Требования, предъявляемые к чертежу
- •Получение изображений на плоскости
- •МетоДы проецирования (рис. 2)
- •Выбор направления проецирования на объект или ориентация объекта относительно плоскостей проекций
- •Комплексный чертЁж
- •Образование комплексного чертежа
- •Комплексный чертёж точки (рис. 4,5) Свойства ортогонального проецирования:
- •Построение точек на комплексном чертеже по координатам (рис. 6)
- •Взаимное расположение точек
- •Конкурирующие точки
- •Рекомендации по решению задач
- •Все задачи решать в два этапа:
- •Уметь выполнять типовые действия (построения), которые встречаются практически в каждой задаче по начертательной геометрии:
- •Свойства ортогонального проецирования (продолжение):
- •Относительное положение прямых Свойства ортогонального проецирования (продолжение):
- •Комплексный чертёж плоскости
- •Относительное положение прямой и плоскости, двух плоскостей
- •Многогранники и тела вращения
- •Пирамида
- •Тела вращения (элементарные) цилиндр
- •Преобразование комплексного чертежа
- •Способ замены плоскостей проекций
- •Способ плоскопараллельного перемещения (рис. 40-41)
- •Вращение вокруг проецирующей прямой
- •Разрез ─ ортогональная проекция предмета, мысленно рассечённого полностью или частично одной или несколькими плоскостями для выявления его невидимых поверхностей.
- •Поверхности
- •Поверхности линейчатые неразвёртываемые
- •Поверхности вращения
- •Позиционные задачи
- •Проецирующие объекты
- •Решение гпз-2, когда один из 2-х пересекающихся объектов занимает проецирующее положение
- •(Общий случай решения позиционных задач)
- •Метод вспомогательных секущих плоскостей
- •Метод вспомогательных секущих сфер
- •Частный случай пересечения поверхностей вращения
- •Аксонометрические проекции
- •Прямоугольная аксонометрия
- •Косоугольная аксонометрия
- •Алгоритм построения аксонометрической проекции
- •Развёртывание поверхностей
- •Графоаналитический способ построения разверток цилиндрических, конических поверхностей [4]
- •Приближённый и условный способы построения разверток поверхностей
- •Введение……………………………………………………………………………………………………………………………………………………………………………………………………………………………..……3 литература……………………………………………………………………………………………………………………………………………………………………………………………………………………..………3
- •Тела вращения (элементарные) ……………………………………………………………………………………………………………………………………………………………………………………21
- •Конус………………………………………………………………………………………………………………………………………………………………………………………………………………………….………22 преобразование комплексного чертежа…………………………………………………………………………………………………………………………………………………………………23
- •Позиционные задачи…………………………………………………………………………………………………………….………………………………………………………………………………………….37
- •Аксонометрические проекции………………………………………………………………..……………………………………………………………………………………………………….……………42
Относительное положение прямых Свойства ортогонального проецирования (продолжение):
Одноимённые проекции параллельных прямых – параллельны (рис. 10, а).
Одноимённые проекции, пересекающихся в пространстве прямых, пересекаются в точках, расположенных на одних и тех же линиях связи (рис. 10, б).
Одноимённые проекции, скрещивающихся в пространстве прямых, пересекаются в точках, расположенных на разных линиях связи (рис. 10, в).
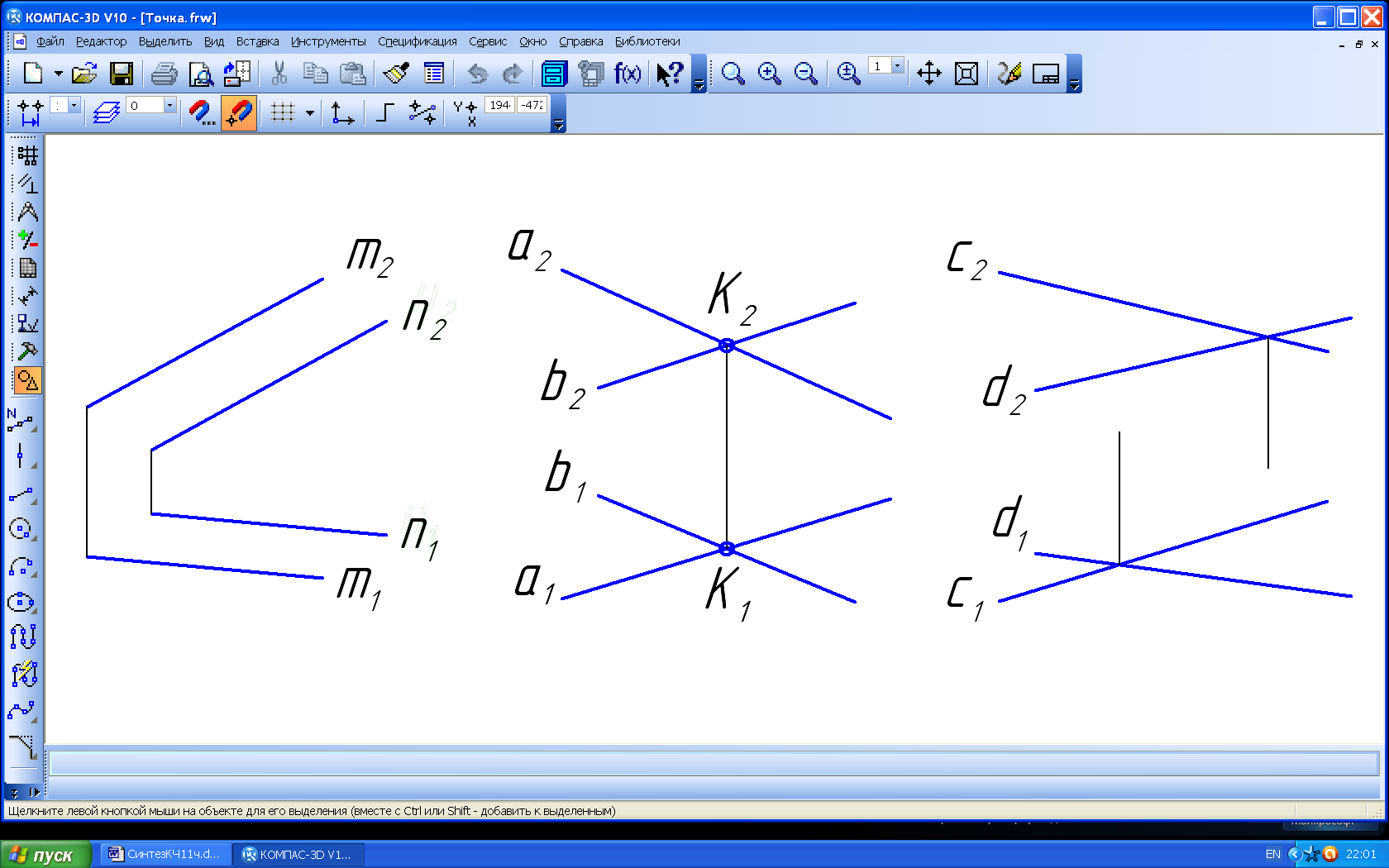
а) б) в)
Рис. 10
Комплексный чертёж плоскости
Плоскость в общем случае может быть задана шестью способами (рис. 11):
а) - тремя точками, не лежащими на одной прямой;
б) - прямой и точкой лежащей вне прямой;
в) - двумя параллельными прямыми;
г) - двумя пересекающимися прямыми;
д) - любой плоской фигурой;
е) - следами. Следы плоскости это линии пересечения плоскости с плоскостями проекций. На рис. 11, е) h1,f2следы, соответственно горизонтальный и фронтальный, плоскости

Рис. 11
2.. В зависимости от ориентации по отношению к плоскостям проекций различают
плоскости общего положения и плоскости частного положения (проецирующие и уровня).
Классификация плоскостей представлена на схеме:
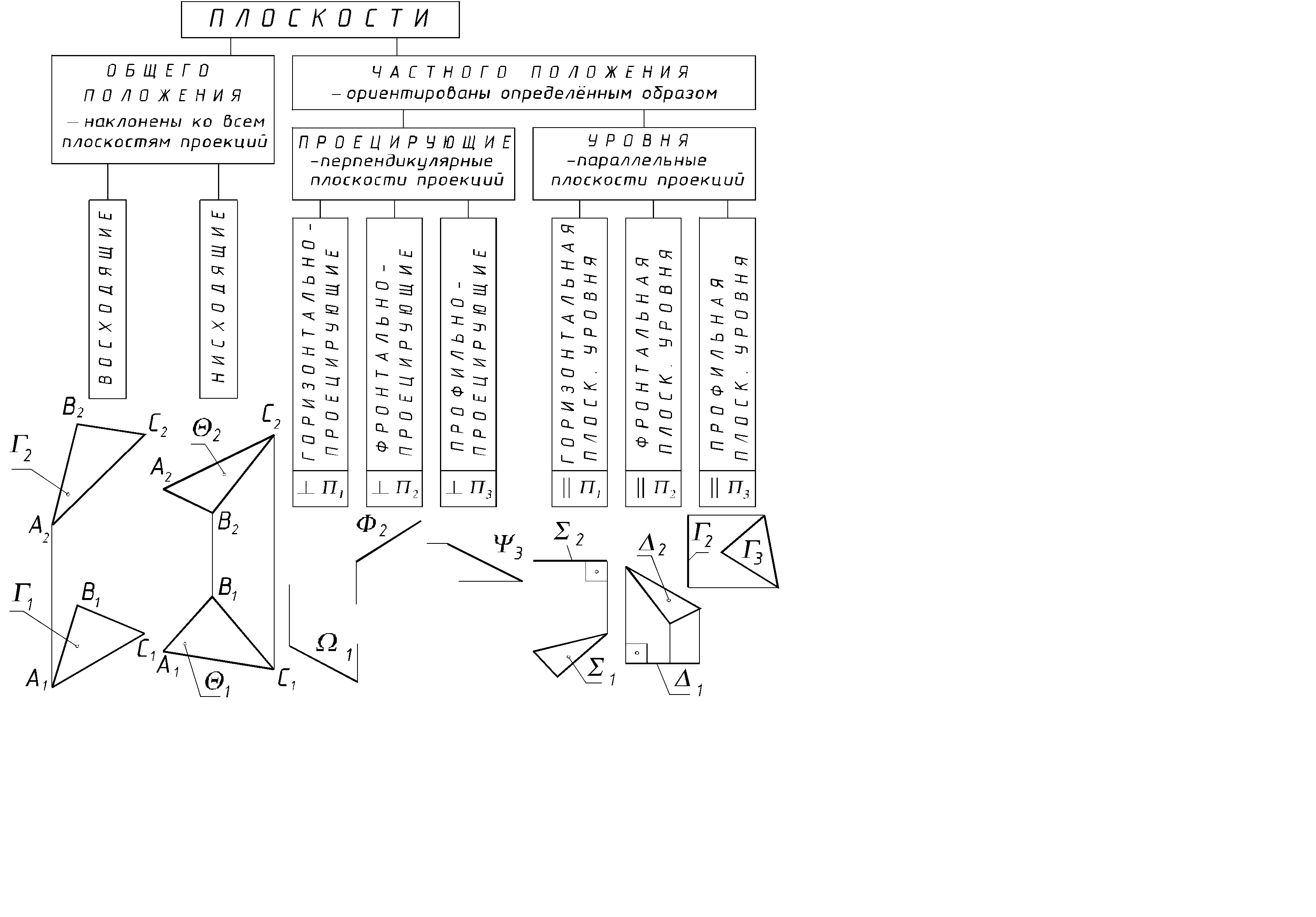
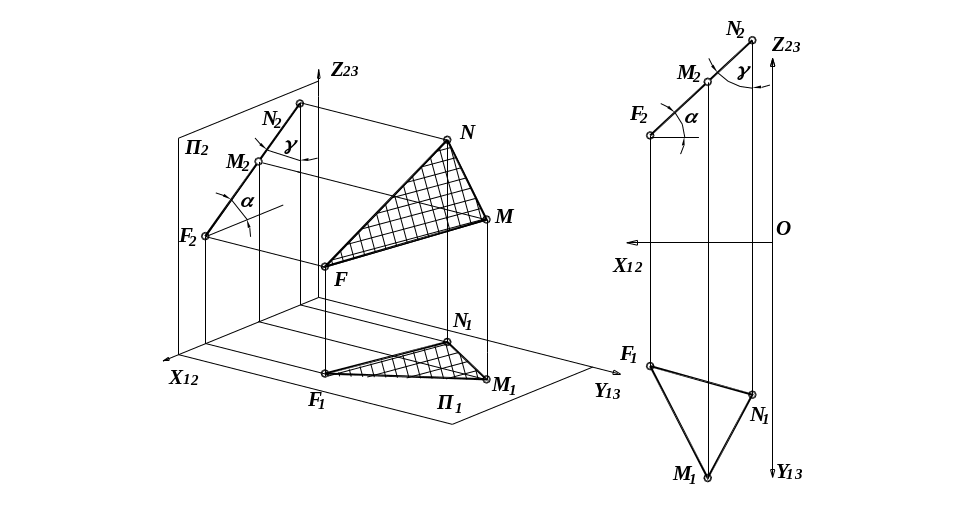
Плоскости общего положения наклонены ко всем плоскостям проекций. Они могут быть восходящими или нисходящими. Формальный признак: если направление обхода вершин треугольника (по часовой или против часовой стрелки) и на горизонтальной и фронтальной проекциях одинаковое, то плоскость восходящая, разное – нисходящая. |
|
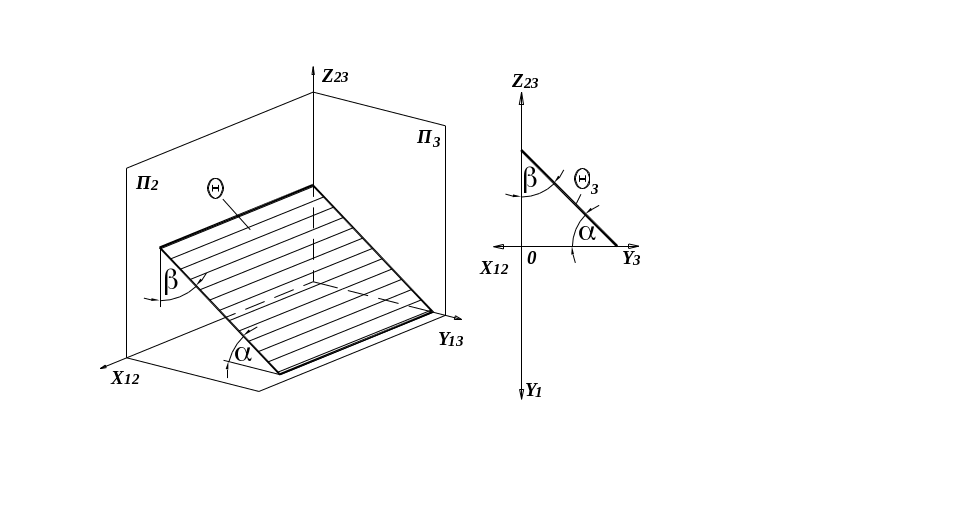
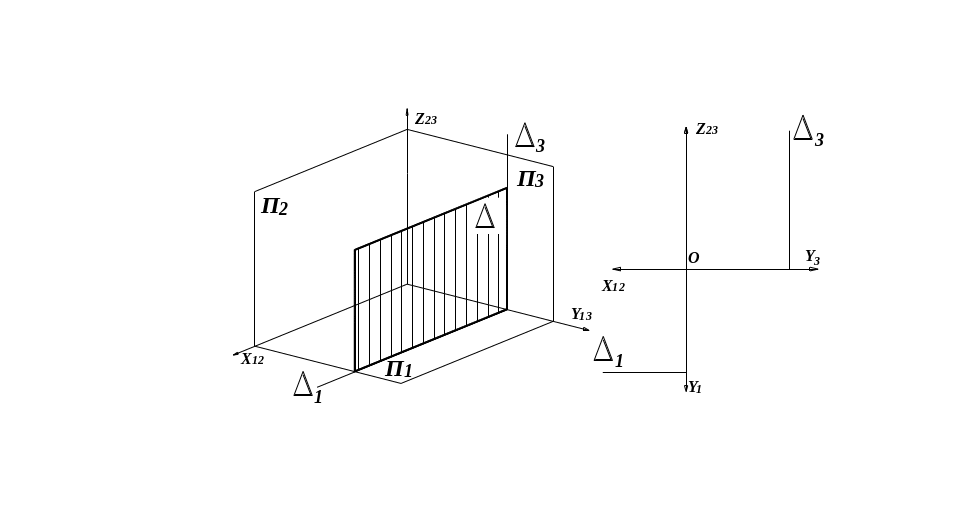
Проецирующие плоскости перпендикулярны к одной из плоскостей проекций. На эту плоскость проекций они (на чертеже) вырождаются в прямые, совпадающие со следами плоскости и определяющие углы её наклона к двум другим плоскостям проекций. След проецирующей плоскости обладает собирательным свойством: – проекции точек, линий и фигур, расположенных в проецирующей плоскости, совпадают со следом одноимённой проецирующей плоскости. Ниже представлены три проецирующие плоскости:
|
горизонтально-проецирующая, фронтально-проецирующая, профильно-проецирующая.
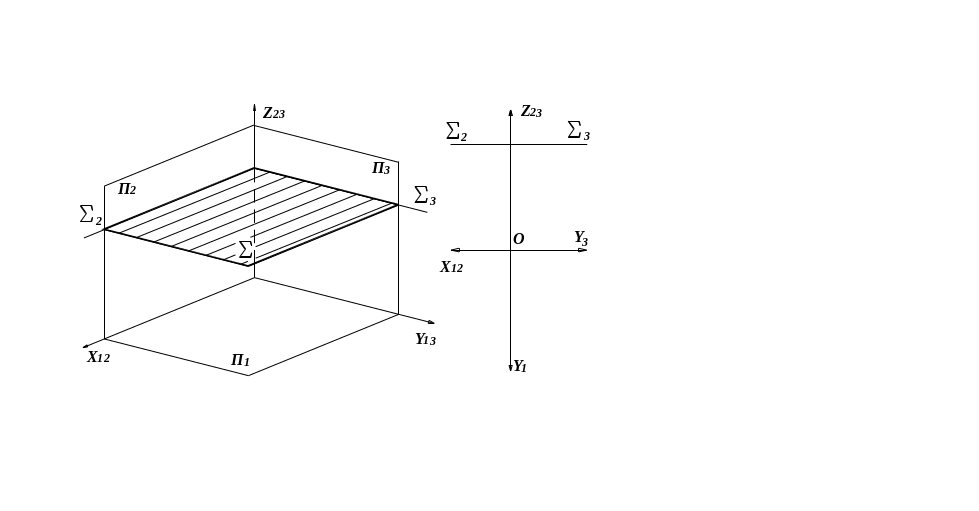
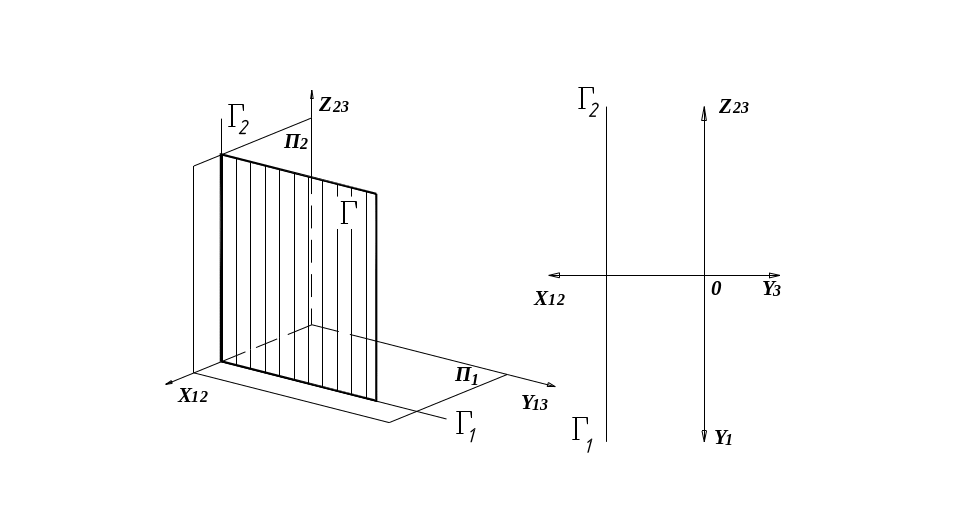
Плоскости уровня параллельны одной из плоскостей проекций и перпендикулярны к двум другим плоскостям проекций (являются дважды проецирующими). На комплексном чертеже их два следа располагаются перпендикулярно к одной и той же координатной оси. Плоская фигура, принадлежащая плоскости уровня, проецируется на параллельную ей плоскость проекций без искажений. Плоскости уровня обычно обозначаются см. ниже.
|
|
|
|
|
Горизонтальная плоскость уровня Фронтальная плоскость уровня Профильная плоскость уровня
Проецирующие плоскости и плоскости уровня можно задать одной вырожденной проекцией.
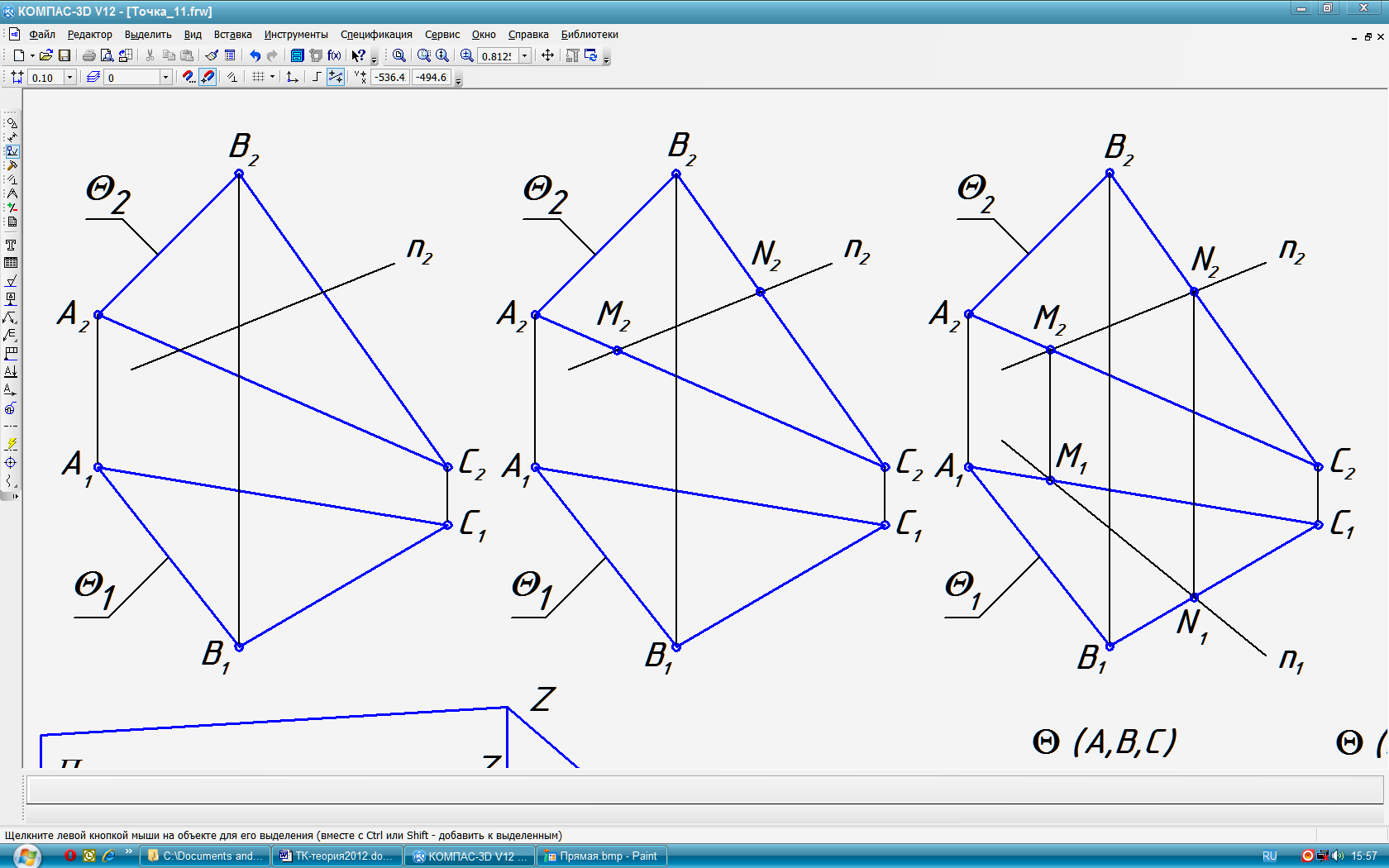
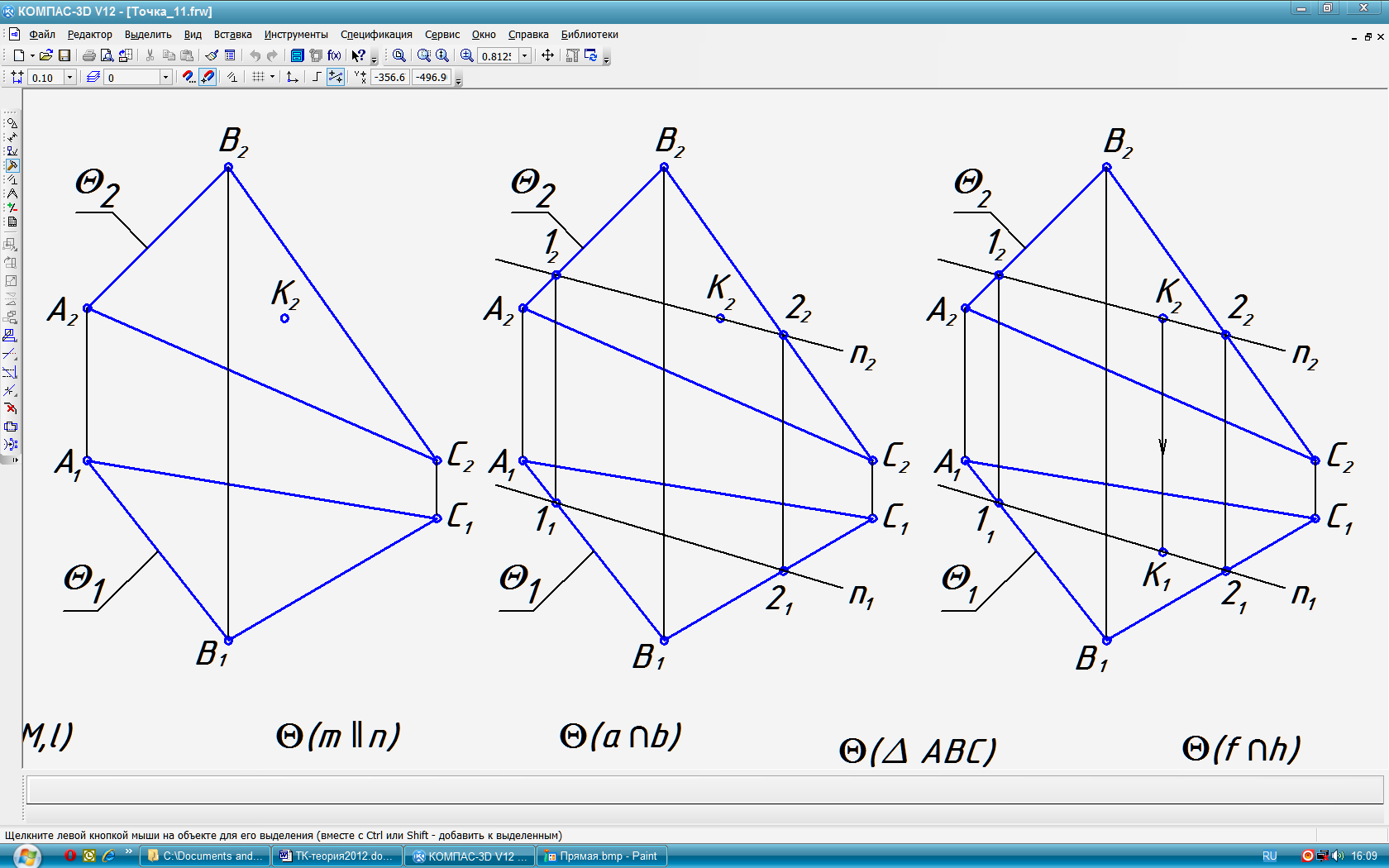
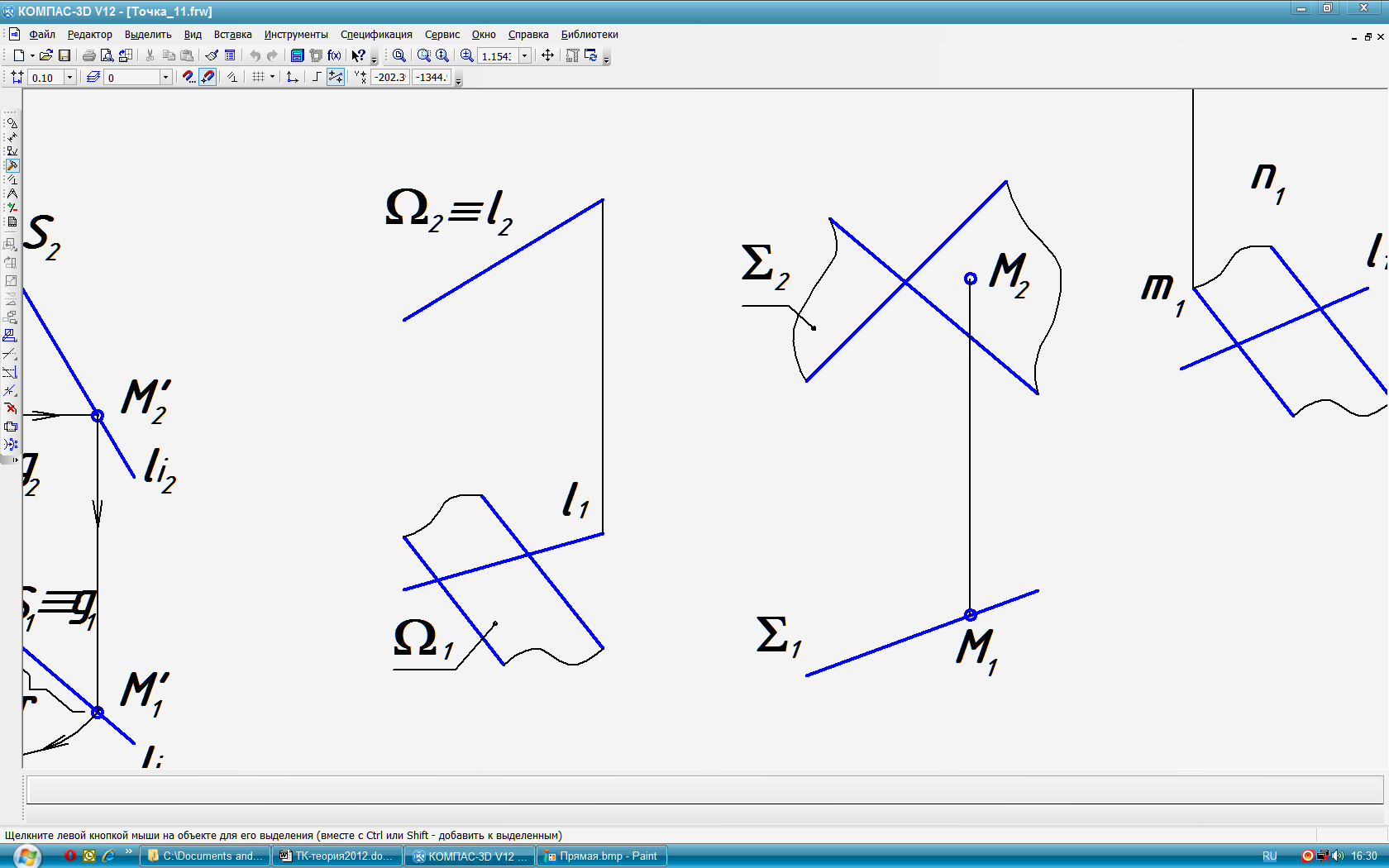
3. Признаки принадлежности прямой плоскости: прямая принадлежит плоскости, если 1) имеет две общие с ней точки. 2) имеет общую с ней точку и параллельна какой-либо прямой плоскости. Признак применяются для построения недостающих проекций прямой линии. Типовая задача 1 (рис. 12): По заданной фронтальной проекции n2 прямой n АВС, построить её горизонтальную проекцию n1. 1) В качестве общих точек берём точки пересечения M и N прямой n со сторонами АВС. 2) Отмечаем на фронтальной проекции общие точки M2 и N2 (рис. 13). 3) По свойству пересекающихся прямых находим горизонтальные проекции точек пересечения M1 и N1 и строим горизонтальную проекцию прямой n1 (рис. 14). 4. Признак принадлежности точки плоскости: точка принадлежит плоскости, если она располагается на прямой, принадлежащей плоскости. Этот признак позволяет строить недостающие проекции точек, принадлежащих плоскости. Типовая задача 2 (рис. 15): Задана фронтальная К2 проекция точки К АВС. Построить её горизонтальную проекцию. 1) Через ()К2 проводим произвольную прямую n2. Отмечаем на ней две общие с плоскостью АВС точки 12 и 22. 2) По линиям связи находим горизонтальные проекции этих точек 11 и 21. Строим горизонтальную проекцию прямой n1 (рис. 16). 3) По линии связи на n1 находим ()К1 (рис. 17). 5. Признаком принадлежности прямой l (рис. 18) и точки M (рис. 19) плоскостям частного положения и является совмещение на чертеже их проекций с одноимёнными следами – проекциями данной плоскости.
Рис. 12 Рис. 13 Рис. 14
Рис. 15 Рис. 16 Рис. 17
Рис. 18 Рис. 19 Рис. 20
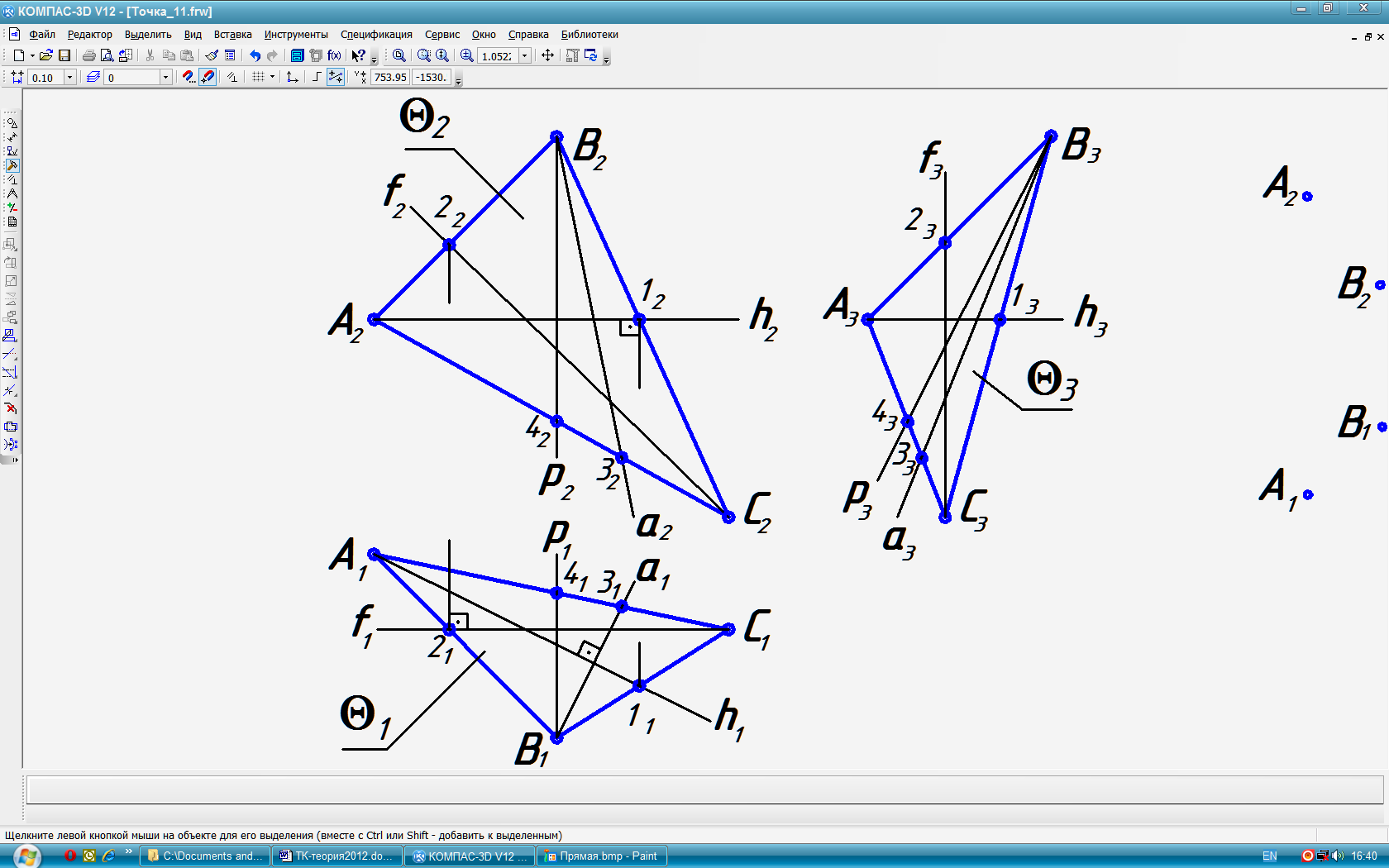
7. В плоскости общего положения можно построить особые прямые: прямые уровня – горизонталь, фронталь и профильную, а также линии наибольшего наклона плоскости к плоскостям проекций (рис. 20). h – горизонталь плоскости – прямая заданной плоскости и ║ плоскости 1.. Построение начинают с фронтальной проекции, которая вертикальной линии связи. f – фронталь плоскости – прямая заданной плоскости и ║ пл. 2. Построение начинают с горизонтальной проекции, которая вертикальной линии связи. p – профильная прямая уровня плоскости – прямая заданной плоскости и ║ пл. 3. Фронтальная и горизонтальная её проекции совпадают с вертикальной линией связи. а – линия ската или наибольшего наклона заданной плоскости к пл. 1. Построение линии начинают с горизонтальной проекции, которая горизонтальной проекции горизонтали. |
|
|
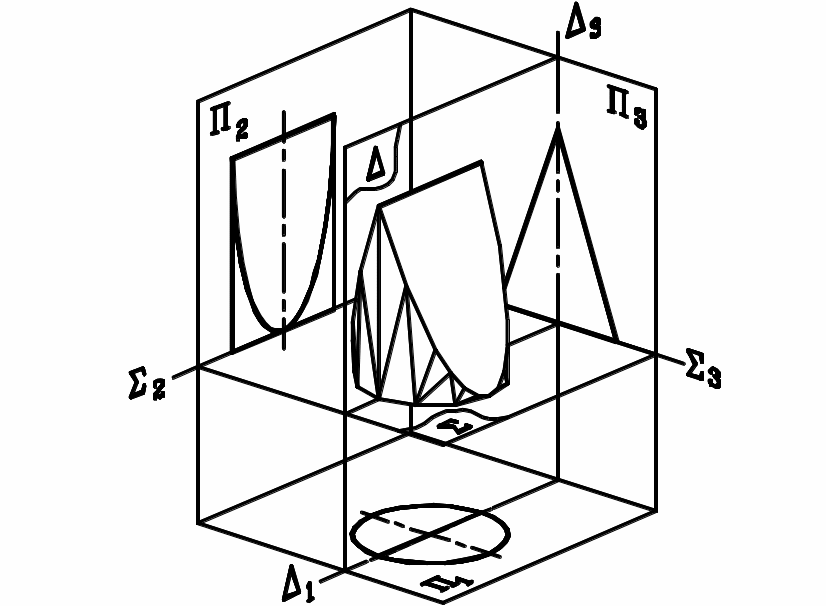
БАЗОВЫЕ ПЛОСКОСТИ (рис.21) это три прозрачные плоскости уровня ║1 , ║2 , ║3 , связанные с объектом или расположенные рядом с ним, и являющиеся базой для отсчёта размеров объекта при его построении (рис. 22, а). На комплексном чертеже каждая базовая плоскость изображается в виде двух базовых прямых линий 2, 3 или 1, 3 или 1,2 , от которых удобно откладывать размеры соответственно по высоте (h), ширине (b) и длине (l) объекта. В отличии от системы координат каждую базовую плоскость можно использовать в отдельности для построения профильных и дополнительных проекций объекта, сечений и видов. Так, например, применение базовой плоскости (1,3) обеспечивает более точное построение профильной проекции, чем постоянная прямая чертежа (рис. 22, б).
Рис. 21 |
|
|
|
|
|
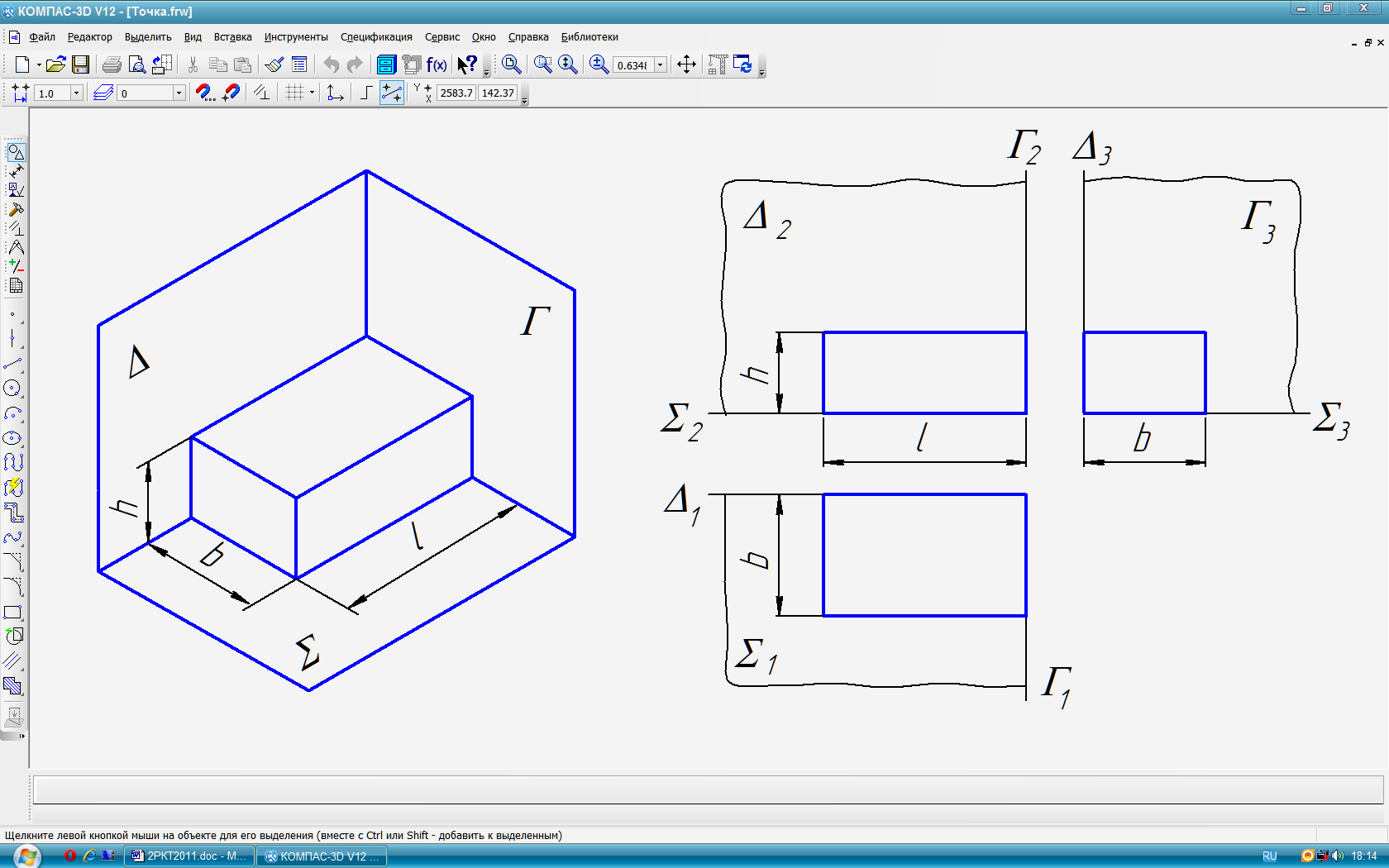
а) б)
Рис. 22

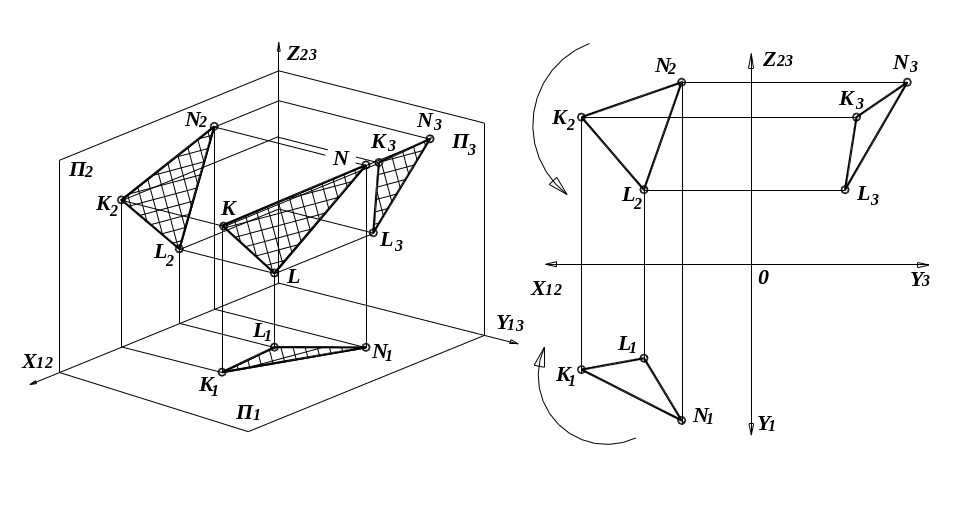 Нисходящая
плоскость
Нисходящая
плоскость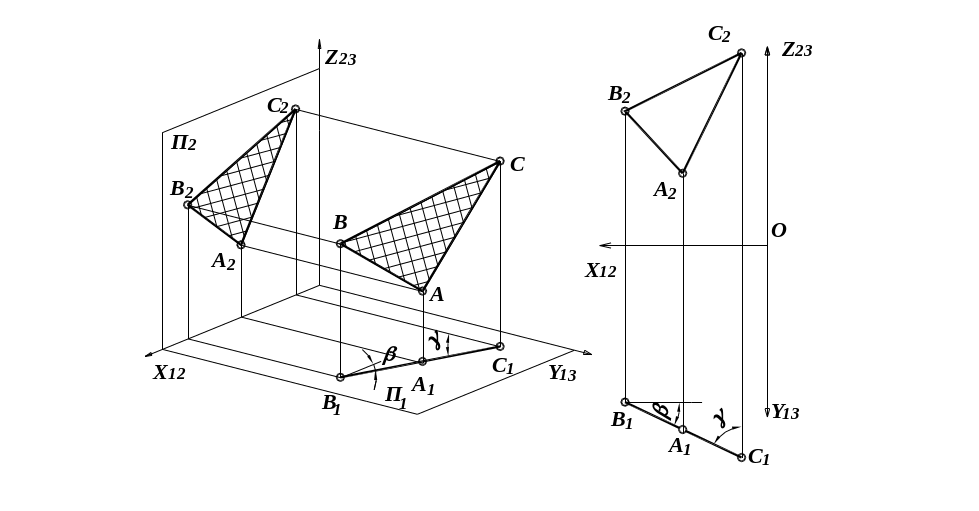
 §
§