Рекомендации по решению задач

1. Все задачи решать в два этапа:

I-й этап - в пространстве.

1) Создать наглядные модели объектов (из картона, пенопласта и др.) или виртуальные.

2) Придать моделям заданные положения в системе плоскостей проекций и выполнить (реально или мысленно) геометрическое действие (преобразование) в соответствии с условием задачи. (Для небольших объектов можно использовать модель плоскостей проекций представленную в приложении (с. 49)).

II-ой этап - на комплексном чертеже.

1) Построить исходные объекты, обозначить объекты и их элементы, .записать кратко условие задачи (Дано… Построить…).

2) На проекциях объектов выполнить геометрическое действие (преобразование) в соответствии с условием задачи.

3) Определить видимость элементов объектов.

Для сложных задач рекомендуется построения предварительно выполнять на черновике, чтобы рационально скомпоновать чистовой чертёж.

2. Уметь выполнять типовые действия (построения), которые встречаются практически в каждой задаче по начертательной геометрии:

1) построение 3-й проекции по двум остальным;

2) построение недостающих проекций точек, принадлежащих плоскости или поверхности;

3) определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций (разными способами);

4) определение расстояния от точки до плоскости;

5) определение натуральной величины плоской фигуры;

6) определение точки пересечения прямой с плоскостью;

7) определение видимости элементов объекта и др.

КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПРЯМОЙ ЛИНИИ (рис. 8)

Свойства ортогонального проецирования (продолжение):

1. Проекция прямой в общем случае – прямая линия.

2. Если прямая параллельна направлению проецирования, то она проецируется в точку. Такая проекция прямой обладает собирательным свойством: все точки прямой проеци­руются в одну точку.

3. Проекция точки, принадлежащей некоторой прямой, принадлежит проекции этой прямой. (Если ()Ка  К₁а₁ , К₂а₂ , К₃а₃ (См. рис. 8)).

4. Проекция точки на отрезке делит проекцию отрезка в том же отношении, в каком точка делит отрезок. (АК/КВ=А₁ К₁ /К₂ В₂=А₂ К₂ /К₂ В₂=А₃ К₃ /К₃ В₃.).

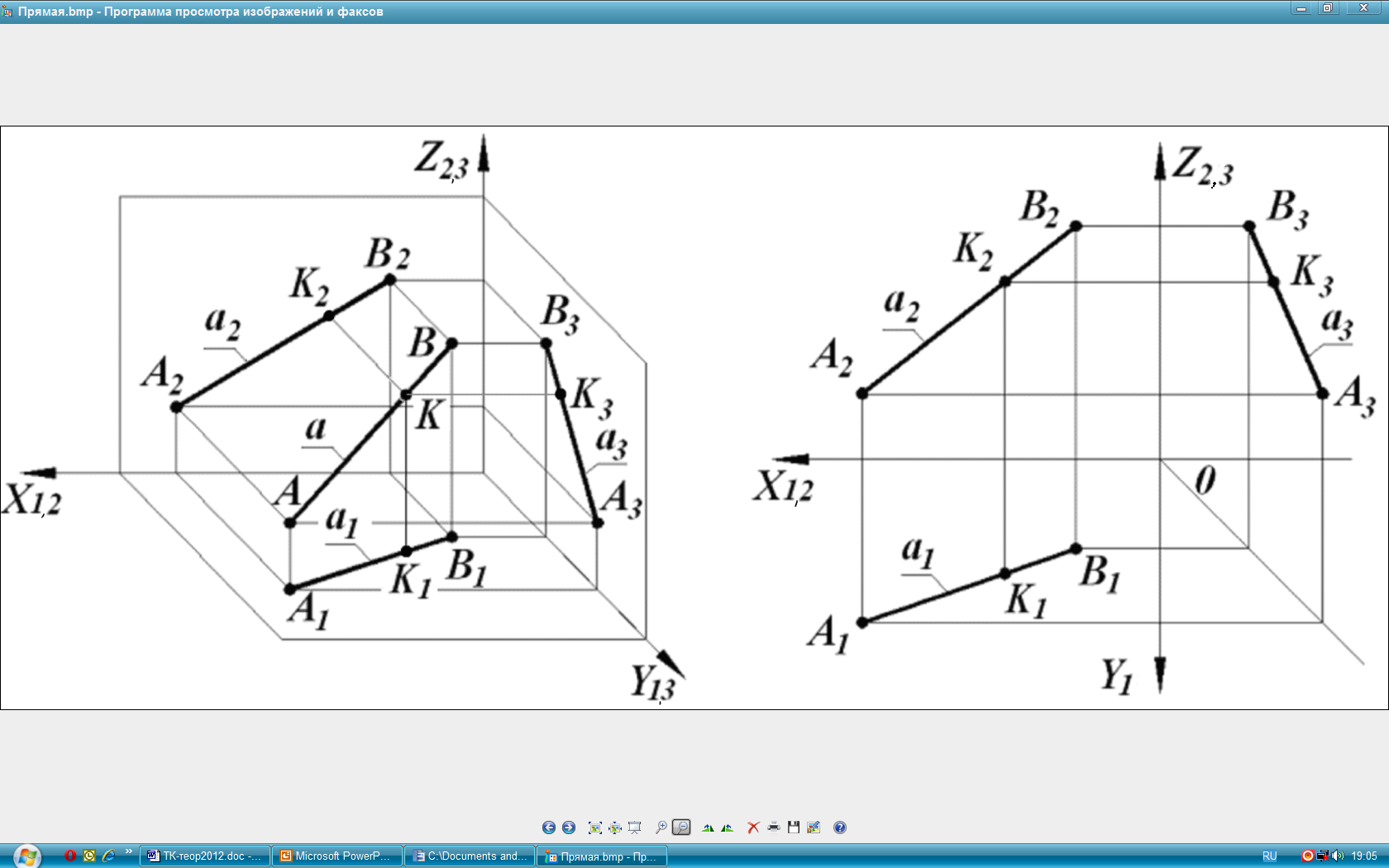
Рис. 8

5. Прямая общего положения может задаваться своими проекциями (рис. 8) или следами (рис. 9). Точки пересечения прямой с плоскостями проекций называются следами и определяются как особые точки прямой, одна из координат которых равна нулю (точки М₁ и N₂ ).

а) б)

Рис. 9

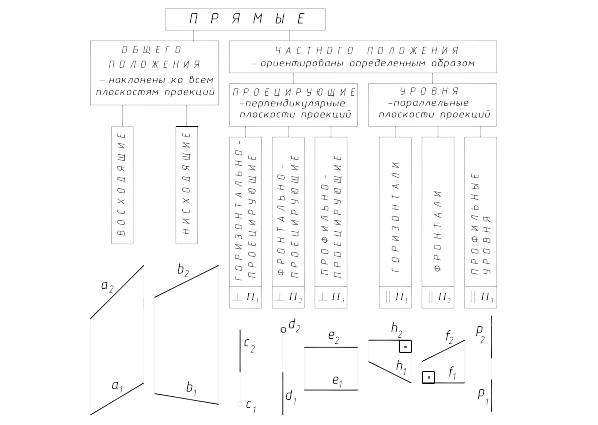
Классификация прямых в зависимости от их положения относительно плоскостей проекций представлена на схеме.

Определение натуральной величины отрезка прямой общего положения

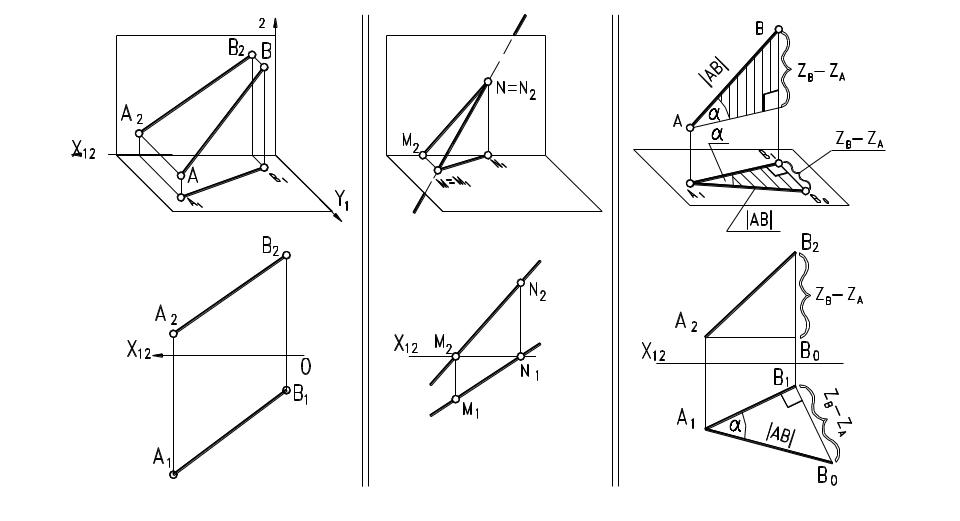
Натуральная величина отрезка прямой общего положения ∣АВ∣ определяется величиной гипотенузы прямоугольного треугольника, один катет которого – одна из проекций, а другой равен разности координат концов отрезка относительно плоскости проекций, на которой делается построение.  – угол наклона прямой АВ к П₁..

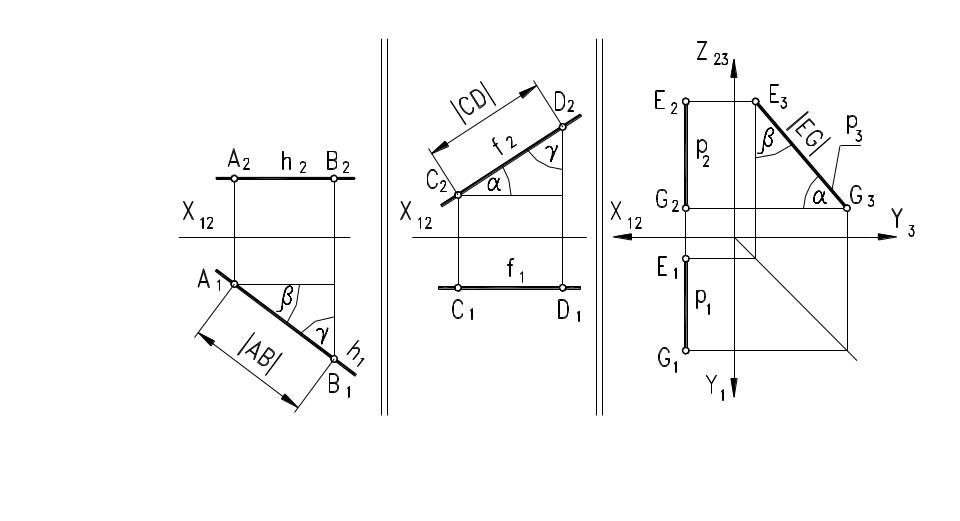
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ

Это прямые, совпадающие с направлением проецирования, а, следовательно, перпендикулярные к одной и параллельные двум другим плоскостям проекций. Одна её проекция вырождается в точку и обладает замечательным собирательным свойством. Две другие проекции равны натуральной её величине. Эти прямые одноимённы перпендикулярной к ним плоскости проекций и получили названия:.

Горизонтально- Фронтально- Профильно-

проецирующая проецирующая проецирующая

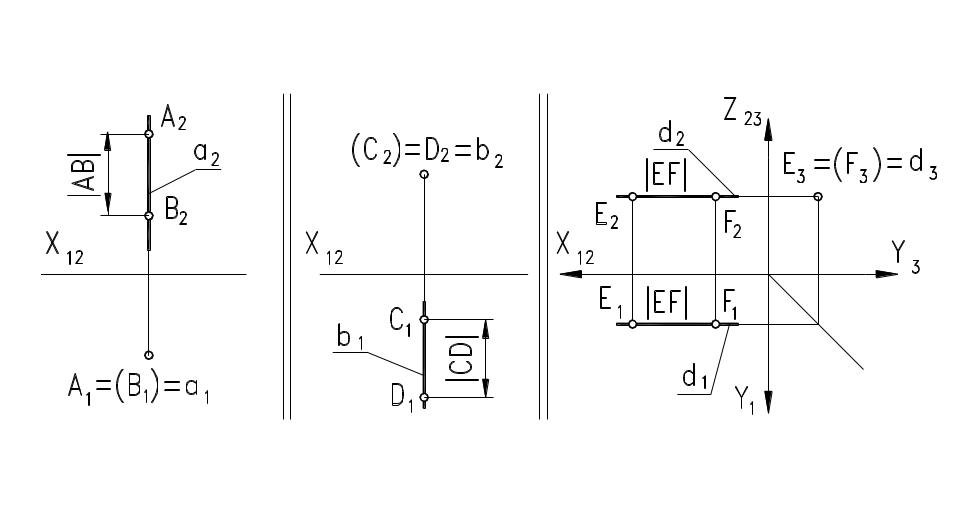
Точки, расположенные на одной проецирующей прямой называются конкурирующими.

ПРЯМЫЕ УРОВНЯ

Если прямая параллельна только одной из плоскостей проекций, то она называется прямой уровня. На параллельную ей плоскость проекций прямая уровня и углы её наклона к двум другим плоскостям проекций проецируются в натуральную величину. Две другие её проекции располагаются перпендикулярно к проекциям направлений проецирования (линиям связи)

h-горизонталь, h || П1, Z2=const

f-фронталь, f || П2, Y1= const

p-профильная, p || П3, X1= const