МетоДы проецирования (рис. 2)

классифицируют в зависимости от угла, наклона проецирующих лучей l к плоскости проекций .

Центральное проецирование (l ^  ─ var, рис. 2, а).

позволяет получить наглядные, но трудно обратимые чертежи. Используется для изображения крупных объектов и сооружений, например, в архитектурно-строительном деле (изображения в перспективе).

Параллельное проецирование (l   , рис. 2, б)

является частным случаем центрального, когда центр проекции (O) отнесён в бесконечность. Используется для построения наглядных чертежей (косоугольные аксонометрические проекции). При этом два измерения объекта располагаются параллельно аксонометрической плоскости и проецируются на неё без искажений.

Косоугольную аксонометрию удобно использовать для изображения тел вращения, так как окружности, расположенные параллельно аксонометрической плоскости в этом случае не искажаются.

Прямоугольное (ортогональное) проецирование (l  , рис. 1, 2, в, г)

 частный случай параллельного проецирования, когда направление проецирова­ния перпен­дикулярно плоскости проекций. Ортогональное или прямоугольное проецирование является основным методом построения изображений в технике и позволяет получать как двумерные (без искажений) проекции объекта, так и трехмер­ные наглядные (аксонометрические) проекции объекта.

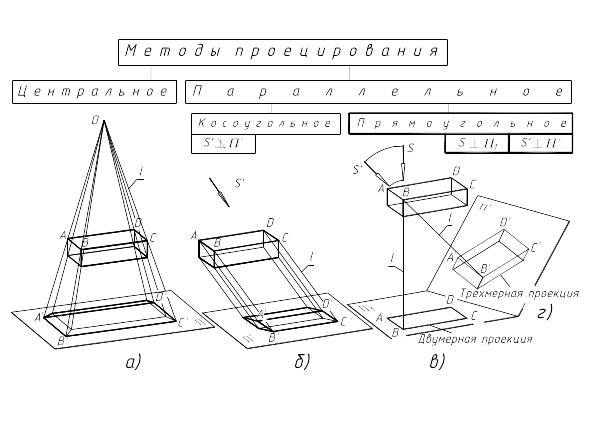
О - центр проецирования; S, S’ - направления проецирования (совпадающее с одним измерением объекта, не совпадающее ни с одним его измерением); l - проецирующие лучи; ₁ ,  ’ плоскости проекций (горизонтальная, аксонометрическая); объект - прямоугольный параллелепипед; A, B, C, D - характерные точки верхней грани параллелепипеда; A₁ , B₁ , C₁ , D₁ и A’, B’, C’, D’ - проекции характерных точек на плоскостях проекций (горизонтальной, аксонометрической)

Рис. 2

Выбор направления проецирования на объект или ориентация объекта относительно плоскостей проекций

существенно влияет на искажение его размеров на чертеже и его наглядность (кроме сферы). Так, например, для прямоугольного параллелепипеда при совпадении направления проецирования с одним его измерением (высотой), два других его измерения (длина и ширина) проецируются без искажений, образуя двумерное (плоское) адекватное объ­екту изображение, но недостаточно наглядное (рис. 2, в). Такие проекции объекта называют вырожденными (одно измерение равно нулю). Из таких изображений, как правило, формируются комплексный чертёж. Если же направление про­ецирования не совпадает ни с одним измерением объекта, то формируются его трехмерное (объемное) изображение, но с искажениями размеров. Такие изо­бражения объекта называются наглядными или аксонометрическими (рис. 2, г).

Комплексный чертЁж

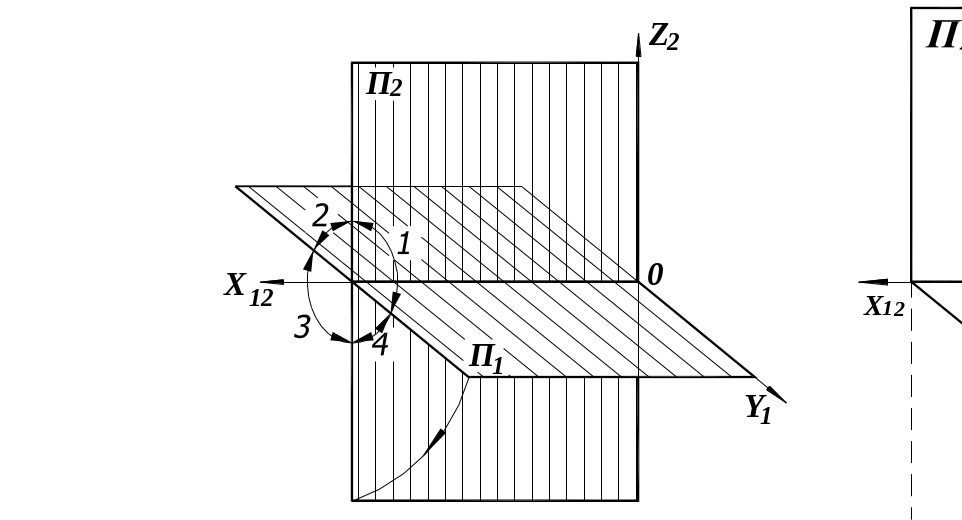
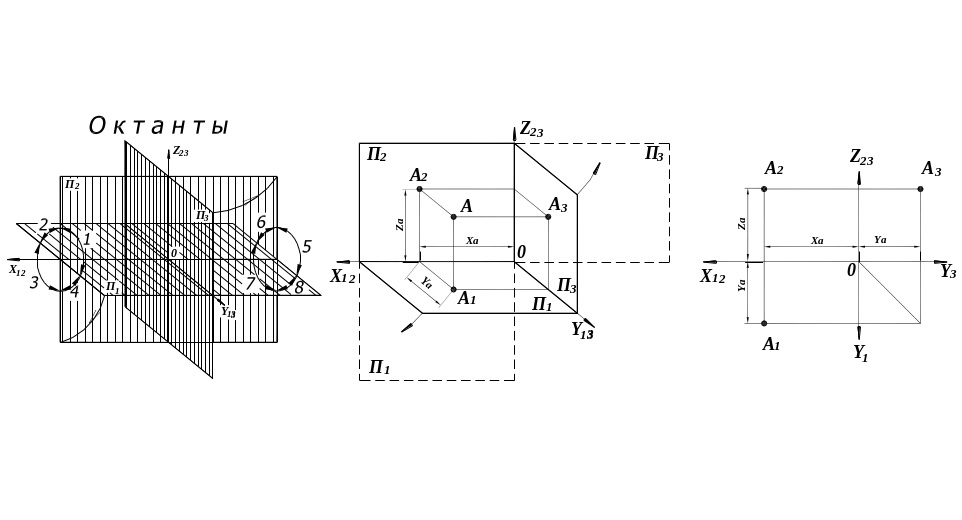
Чертёж, со­стоящий из одной двумерной проекции объекта, не явля­ется обратимым, так как отражает только два измерения объекта из трёх. Этот недос­таток можно устранить, если использовать чертежи с числовыми отметками (например, топографические), или проецировать объект на несколько плоскостей проекций, располагая его в квадранте или октанте (рис. 3). Две взаимно-перпендикулярные плоскости проекций П₁  горизонтальная и П₂  фронтальная де­лят пространство на четыре части, называемые квадрантами (рис. 3, а). Три взаимно-перпендикуляр­ные плоскости проекций (добавлена П₃  профильная) делят пространство на восемь час­тей  октантов (рис. 3, б).

Изображение объекта методом прямоугольного проецирования на две или более плоскости проекций называется комплексным чертежом (эпюр Монжа).

Для точного задания и построения точек на комплексном чертеже используется гло­бальная и локальная система координат. Начало глобальной системы координат сов­падает с точкой пересечения плоскостей проекций, а координатные оси с линиями пересе­чения плоскостей проекций (рис. 3). Локальная система координат связана с объектом (рис. 109).

Положение точки в пространстве характеризуется тремя координатами, которые получили в начертательной геометрии следующие названия: X  широта, Y  глубина, Z  высота.

	а) квадранты б) октанты Рис. 3