Приближённый и условный способы построения разверток поверхностей

Сущность способа заключается в том, что в трудно развёртываемую (как в данной задаче) или неразвёртываюемую поверхность (например, сферу) вписывают подходящую развёртываемую поверхность (гранную, цилиндрическую, коническую или их комбинацию) и строят её развёртку. Далее, через концы рёбер или образующих вписанной поверхности, проводят плавную кривую, завершающую контур развёртки: приближённой для трудно развёртываемой поверхности или условной для неразвёртываемой поверхности.

Типовая задача 20 (рис. 117 слева): Построить развёртку боковой поверхности наклонного эллиптического конуса. Решение (рис. 117 справа и внизу):

1. В конус вписываем пирамиду SABC (чем больше боковых граней, тем точнее развёртка конуса).

2. Строим развёртку пирамиды (см. рис. 114).

   0. Методом вращения вокруг проецирующей оси i определяем натуральные величины рёбер SB, SC – отрезки S’₂ B’₂ и S₂ C’₂. Рёбра SA, SD являются фронталями. S₂A₂, S₂D₂ – их натуральные величины.

   1. Задаём линию разрезки поверхности по ребру SD. Ось симметрии развёртки – ребро SA.

   2. Построение развёртки начинаем с оси симметрии, на которой откладываем натуральную величину ребра SA – S₀A₀ . Далее тонкими линиями последовательно строим треугольники A₀S₀B₀, S₀B₀C₀, S₀C₀D₀ (методом засечек по трём сторонам). Боковые рёбра пирамиды есть образующие конуса. Левую часть развёртки строим, используя её симметричность.

3. Строим развёртку конуса, соединяя концы боковых ребер D₀, C₀, B₀, A₀ и т.д. плавной кривой.

4. Перенос произвольной точки М с поверхности конуса на развёртку производим с помощью дополнительной образующей конуса SN и аналогичных действий (пункты 2.1, 2.3).

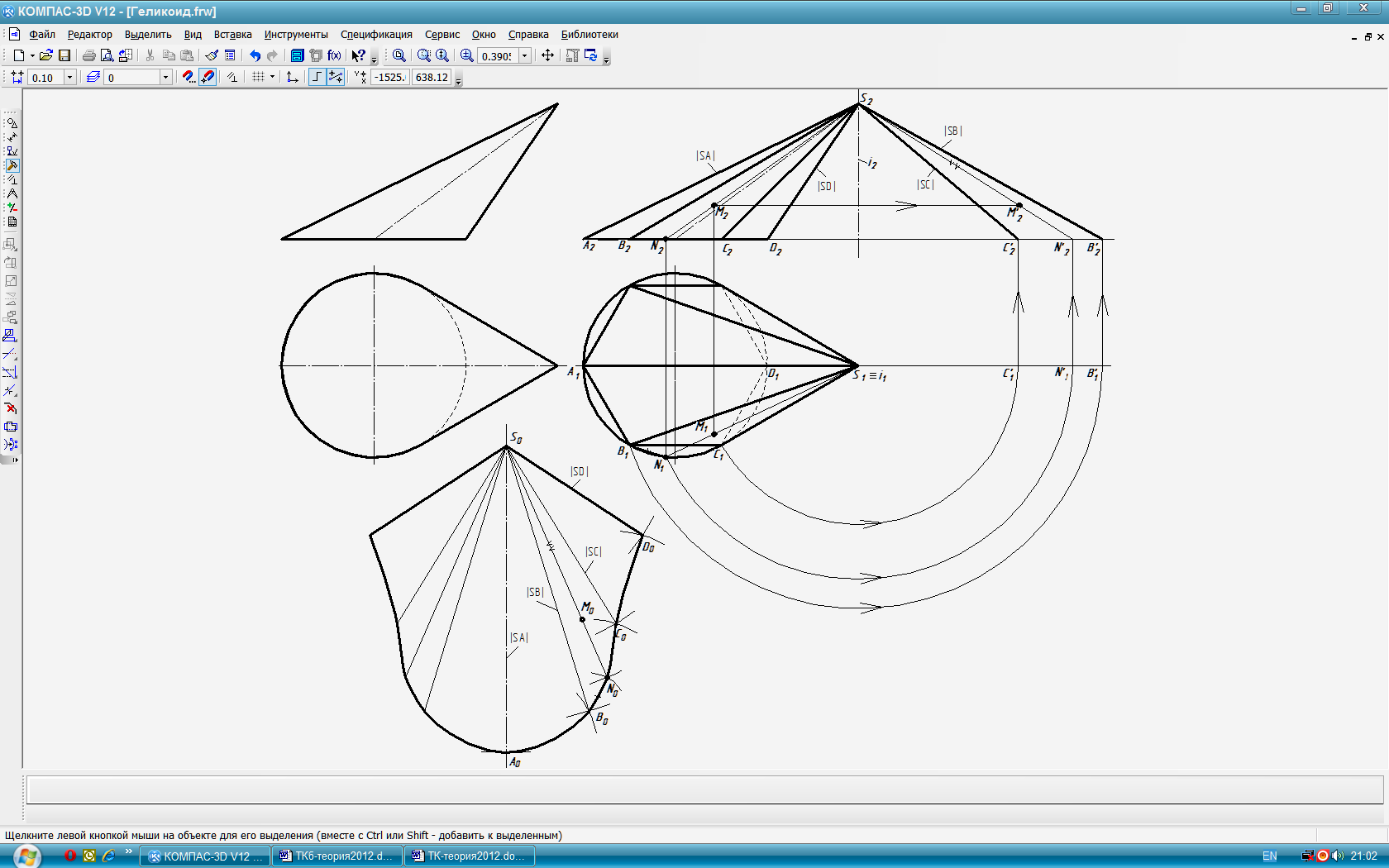Рис. 117

СОДЕРЖАНИЕ

Введение……………………………………………………………………………………………………………………………………………………………………………………………………………………………..……3 литература……………………………………………………………………………………………………………………………………………………………………………………………………………………..………3

Основы начертательной геометрии………………………………………………………………………………………………………………………………………………………………………….…4

Получение изображений на плоскости………………………………………………………………………………………………………………………………………………………………………5

МЕТОДы проецирования………………………………………………………………………………………………………………………………………………………………………………….…………………5

комплексный чертЁж……………………………………………………………………………………………………………………………………………………………………………………………..…….……..7

КОМПЛЕКСНЫЙ ЧЕРТЁЖ ТОЧКИ………………………………………………………………………………………………………………………………………………………………..……………………….….7

Построение точек на комплексном чертеже по координатам…………………………………………….………………………………………………………………………..8

Конкурирующие точки……………………………………………………………………………………………………………………………………………………………………………….…………………9

РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ……………………………………………………………………………………………………………………………………………………………..…………………9

КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПРЯМОЙ ЛИНИИ…………………………………………………………………………………………………………………………………..…………………………………….…10

Определение натуральной величины отрезка прямой общего положения…………………………………………………………………………………………………..……11

ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ…………………………………………………………………………………………………………………………………………………….……………………..…..…12

ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ…………………………………………………………………………………………………………………………………………………………………………………….…….……12

ПРЯМЫЕ УРОВНЯ………………………………………………………………………………………………………………………………………………………………………………………………………….……12

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ………………………………………………………………………………………………………………..………………………………………….…..…13

КОМПЛЕКСНЫЙ ЧЕРТЁЖ плоскости…………………………………………………………………………………………………………………………………………………………….……………………13

БАЗОВЫЕ ПЛОСКОСТИ……………………………………………………………………………………………………………………………………………………………………………………………………17

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ……………………………………………………………………………………………………………17

Перпендикулярность прямой и плоскости, двух плоскостей..………………………………………………………………………………………………………………………………17

МНОГОГРАННИКИ И ТЕЛА ВРАЩЕНИЯ………………………………………………………………………………………………………………………………………………………………………………18

Призма…………………………………………………………………………………………………………………………………………………………………………………………………………………………………19

Пирамида……………………………………………………………………………………………………………………………………………………………………………………………….……………………………20