Развёртывание поверхностей

Если рассматривать поверхность как тонкую, гибкую, нерастяжимую плёнку, то, неко­торые из поверхностей можно путём изгибания совместить с плоскостью развёртки без раз­рывов и складок. Поверхности, обладающие этим свойством, называют развёртывающимися (по­верхности многогранников, цилиндрические, конические и торсовые), а фигуру, полученную в ре­зультате совмещения поверхности с плоскостью, - развёрткой. Поверхности, не обладающие этим свойством, называют неразвёртывающимися (сферические, торовые, поверхности с плоскостью параллелизма и др.).

Строить развёртку поверхностей можно графическим, графо-аналитическим и приближённым способами. В общем случае построение развёртки начинают с определения натуральной величины рёбер многогранника или образующих поверхности.

Графические способы построения развёрток гранных поверхностей.

Развёртка призмы способами нормального сечения (рис.112) и раскатки (рис. 113).

Способ нормального сечения (боковые рёбра являются прямыми уровня) основан на том, что задают нормальное сечение призмы (1,2,3), перпендикулярное боковым рёбрам, определяют его натуральная величину, развёртывают его в прямую линию (1₀ ,2₀ ,3_0, ,1₀ ) и перпендикулярно к ней строят боковые рёбра призмы.

Способ раскатки (рёбра боковые и оснований являются прямыми уровня) состоит в последовательном совмещении граней призмы с плоскостью развёртки, проходящей через одно из боковых рёбер, путём вращения каждой грани вокруг ребра уже совмещённого с плоскостью развёртки.

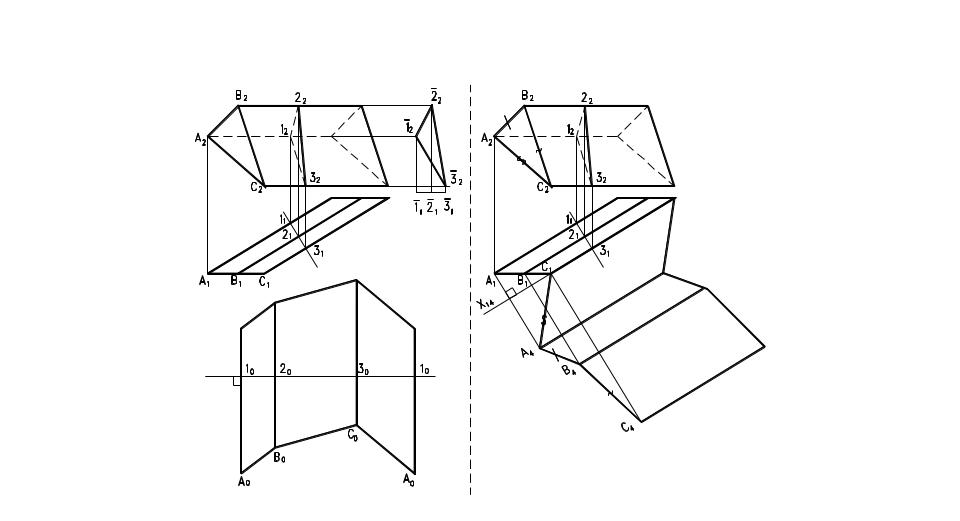
Рис. 112 Рис. 113

Развёртка пирамиды (рис. 114) выполняется путём последовательного построения треугольных боковых граней в натуральную величину (способ триангуляции). Для определения натуральной величины боковых рёбер применяют способ вращения вокруг проецирующей прямой.

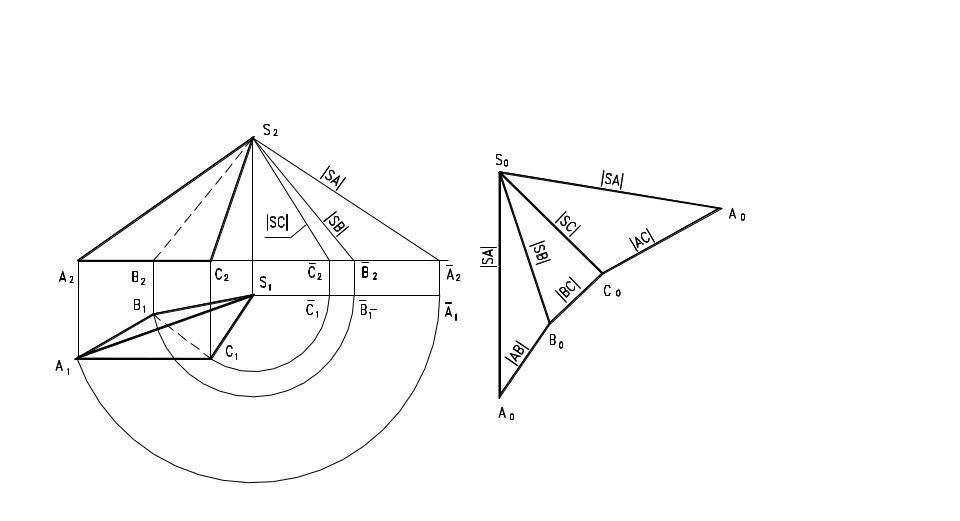
Рис. 114

Графоаналитический способ построения разверток цилиндрических, конических поверхностей [4]

Развертка цилиндра вращения диаметра d и высотой h представляет собой прямоугольник длиной pd и высотой h (рис. 115).

Для построения на развертке линии пересечения цилиндра с фронтально-проецирующей

плоскостью S (S₂), на поверхности цилиндра задается каркас образующих линий.

Рис. 115

Для этого окружность основания цилиндра разбивается на равное число частей (12). На столько же частей делится на развертке отрезок L, равный длине окружности основания цилиндра (L= pd). Через точки деления проводятся совмещенные с плоскостью развертки образующие цилиндра, на которых откладываются их натуральные величины. Полученные точки соединяют плавной кривой n.

При определении на развертке положения произвольной точки поверхности К (К₂,К₁) использован метод аппроксимаций — дуга 4К(4₁ К₁ ) заменена стягивающей ее хордой.

Построение развертки поверхности прямого кругового конуса Ф (S,m) показано на рис. 116.

Развертка представляет собой круговой сектор с углом при вершине, определяемым из условия равенства длины окружности основания конуса длине окружности сектора круга развертки:

где d – диаметр основания конуса;

– длина образующей конуса.

.

Рис. 116

Произвольная точка , принадлежащая поверхности конуса построена на развертке в следующей последовательности:

1) Через заданную точку проведена образующая ;

2) Способом вращения вокруг оси конуса определено натуральное удаление точки M от вершины конуса ;

3) Образующая построена на развертке путем аппроксимации дуги хордой ;

4) Определено положения точки на образующей развертки —