Прямоугольная аксонометрия

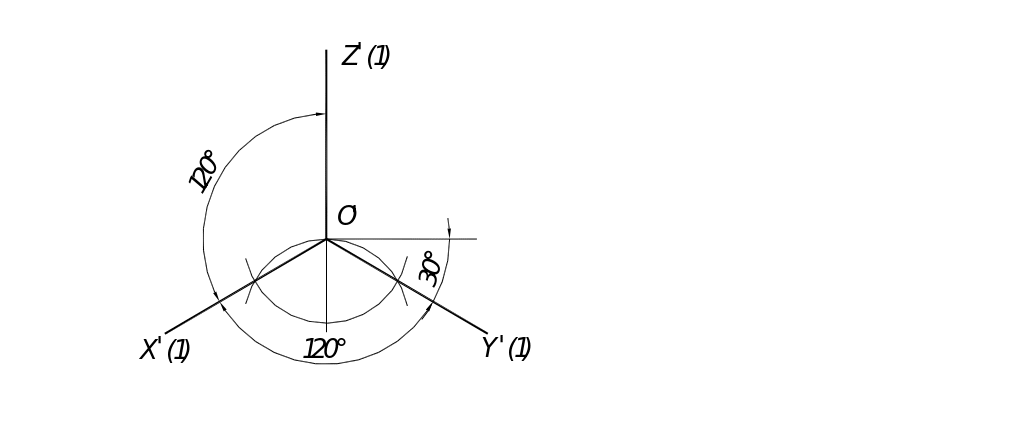
Изометрическая проекция. Аксонометрические плоскости равно наклонены к координатным осям и являются гранями октаэдра. Положение аксономет­рических осей на рис. 100. Углы между аксоно­метрии-ческими осями равны, со­ставляют 120 и строятся с по­мощью циркуля. Приведенные ко­эффициенты ис­кажения: k_x= k_y= k_z=1. Масштаб изображения— 1,22:1.

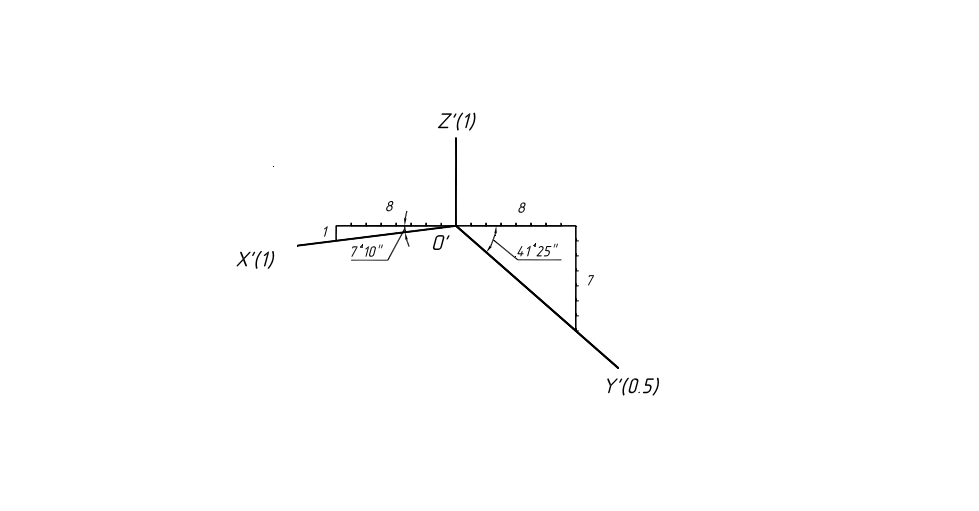
Диметрическая проекция. Положение аксономет­рических осей приве­дено на рис. 101. Оси и строят как гипоте­нузы прямо­уголь­ных треугольников с от­но­шением кате­тов соот­ветственно 1:8 и 7:8. Приведенные коэффи­ци­енты искажения: k_x=k_z=1; k_y=0,5k_x=0,5. Масштаб изобра­же­ния при этом — 1,06:1.

Примечание. В скобках даны значения коэффициентов искажения.

Рис. 100 Рис. 101

Окружности, расположенные в координатных и им па­раллельных плоскостях, изображаются в прямоугольной аксонометрии в виде эллипсов, большие оси которых располагаются перпендикулярно оси, отсутствующей в плоскости окружности.

Размеры эллипсов и расположение осей: в изометрии (рис. 102), в диметрии (рис. 103).

Эллипс в изометрии можно приближенно заменить четырёхцен­тровым овалом.

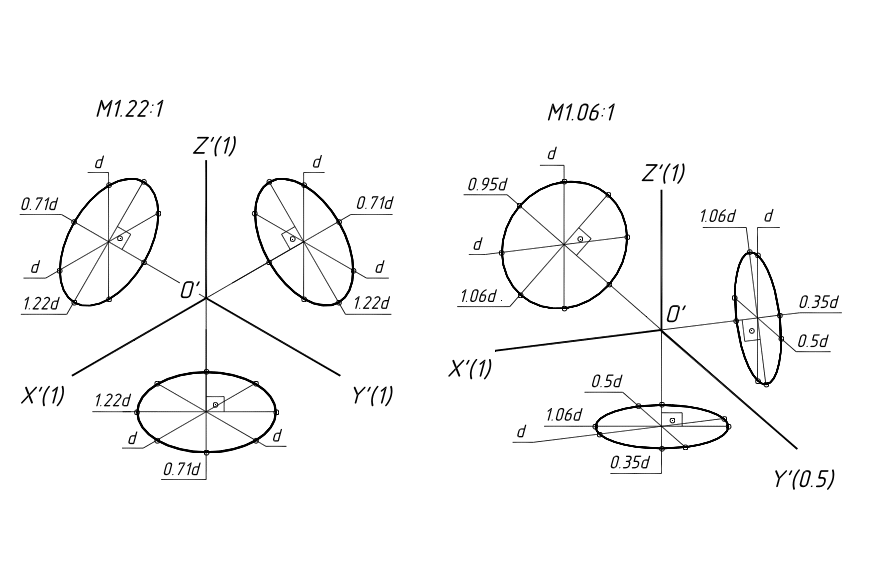
Рис. 102 Рис. 103

Косоугольная аксонометрия

Направление проецирования не пер­пендикулярно аксонометрической плоскости, которая располагается параллельно одной из основных плоскостей проекций, определяющее её название. Элементы объекта, расположенные парал­лельно этой плоскости проекций, не искажаются. Если аксонометрическая плоскость параллельна фрон­тальной плоскости проекций, то имеет место косоугольная фронтальная изометрия или диметрия, если параллельна го­ризонтальной плоскости проекций то — горизонтальная изометрия.

Фронтальная изометрическая проекция (рис. 104): k_x=k_y=k_z=1.

Горизонтальная изометрическая проекция (рис. 105): k_x=k_y=k_z=1.

Фронтальная диметрическая проекция (рис.106): k_x=k_z=1; k_y=0,5k_x=0,5 (строит. чертежи).

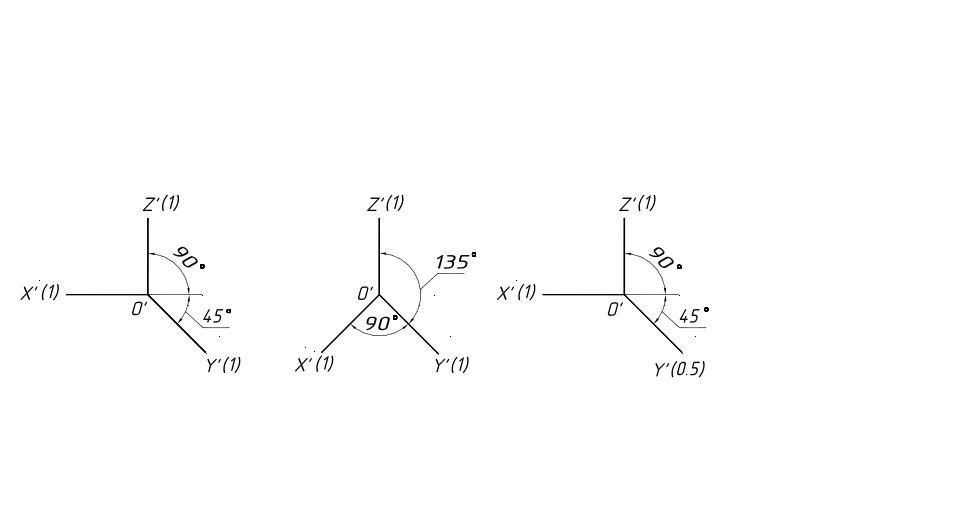
Рис. 104 Рис. 105 Рис. 106

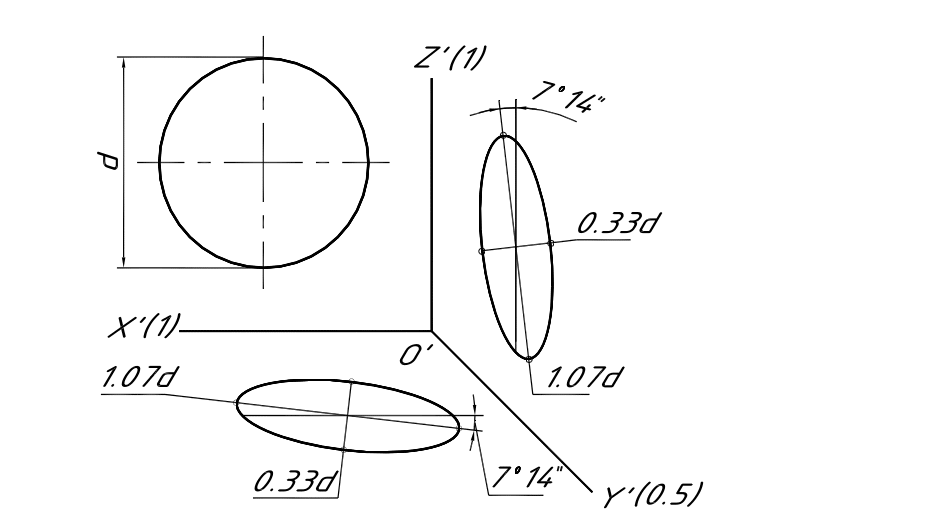
Фронтальную изометрию и диметрию используют для построения тел вращения (коротких и удлинённых), так как окружность и другие элементы, располо­женные в плоскости или ей параллельных, изображаются в ко­соугольной аксонометрии без искажений. Изображения окружностей в косоугольной диметрии, расположенных в координатных плоскостях, представлены на рис. 107.

Горизонтальную изометрию применяют для планировок строительных объектов.

Рис. 107

Алгоритм построения аксонометрической проекции

Исходными данными для аксонометрического чертежа является комплексный чертёж.

1. На комплексном чертеже вводят оси локальной системы координат, совмещая их с ребрами, гранями объекта или осями, плоскостями симметрии;

2. Выбирают вид аксонометрии. Изображают аксонометрические оси – проекции локальных осей на картинную плоскость.

3. Определяют координаты опорных и промежуточных точек.

4. Строят, с учетом коэффициентов искажений, вторичную (плоскую) аксонометриче­скую проекцию объекта (в тонких линиях) по одной из его ортогональных проекций и в дальнейшем сохраняют ее.

5. Строят аксонометрическую проекцию объекта по его вторичной, добавляя третье измерение (координаты Z). Определяют видимость его элементов.

6. Выполняют (при необходимости) разрез объекта, рассекая его двумя или тремя плоскостями, параллельными координатным плоскостям.

Типовая задача 19 (рис. 108 -111): Построить изометрическую проекцию конуса с линией пересечения (рис. 108). Решение (рис. 109 -111):

1. Начало локальной системы координат XOYZ – в центре основания конуса (рис. 109).

2. Изображаем изометрические оси X’O’Y’Z’, указываем в скобках значения коэффициентов искажений, масштаб изображения (рис. 110).

3. Строим эллипс основания конуса одним из способов (например, по 8-и точкам, используя соотношения на рис. 102). Определяем на горизонтальной проекции координаты X,Y опорных и промежуточных точек линии пересечения (см., например, точку 5 на рис. 109) и строим её вторичную (плоскую) проекцию в тонких линиях на пл. X’O’Y’ (рис. 110).

4. Через точки на вторичной (плоской) проекции проводим прямые параллельные оси Z' и отклады­ваем на них высоты точек объекта (см. точку 5), которые берём с фронтальной про­екции (рис. 109). Очерковые образующие конуса касаются эллипса основания. Пространствен­ная линия пересечения не должна выходить за очерк конуса; обводим их основной линией. Вспомогательные построения оставляем в тонких линиях (рис. 111).

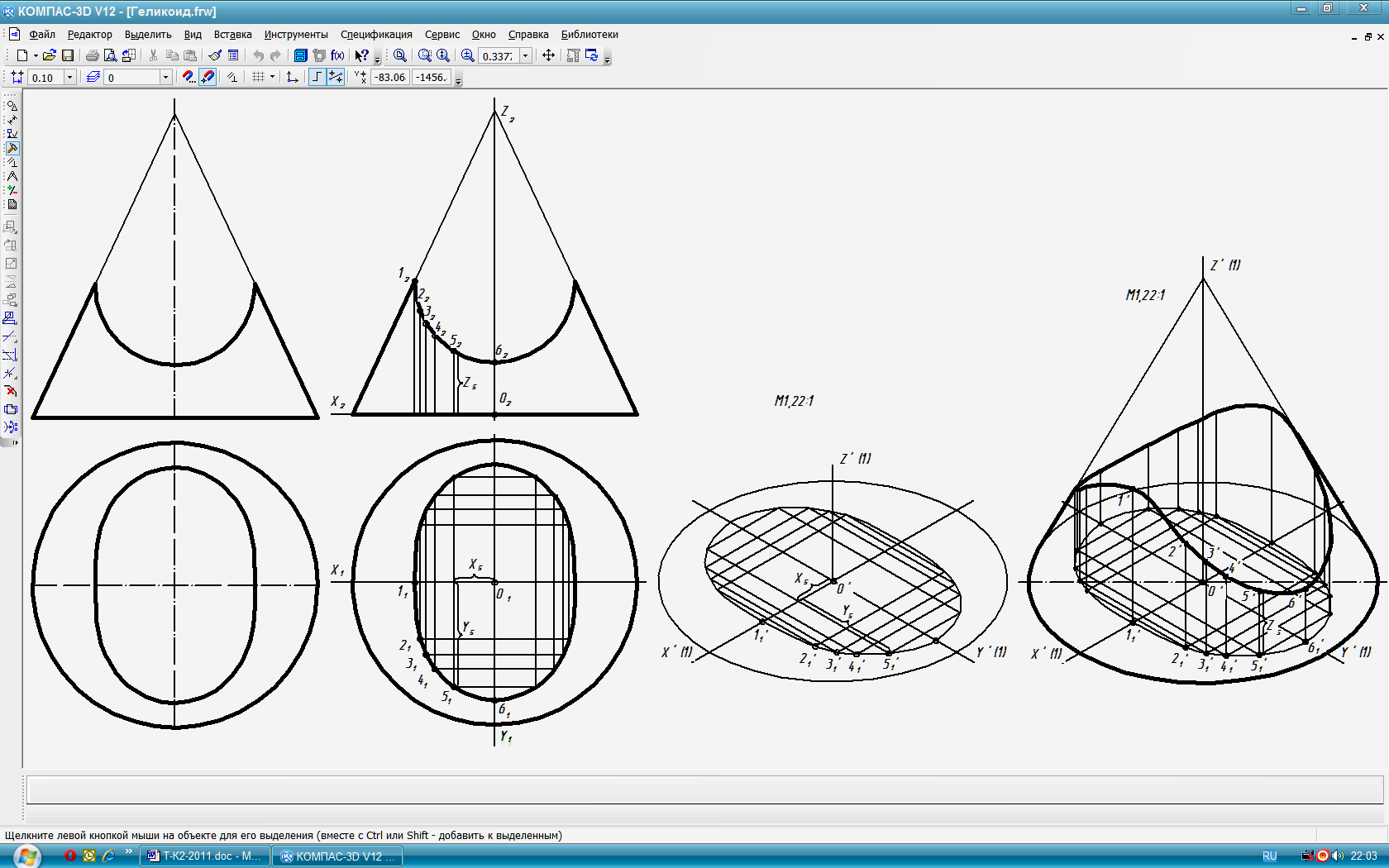
Рис. 108 Рис. 109 Рис. 110 Рис. 111