Метод вспомогательных секущих сфер

применяется для построения линий пересечения поверхностей вращения, оси которых пе-

ресекаются и лежат в плоскостях уровня.

Метод очень эффективен т.к. позволяет за одно построение сферы R_min определить положение линии пересечения, но требует точности в исполнении. Этот метод основан на свойстве сферы, пересекаться с любой поверхностью вращения, ось которой проходит через Рис. 90

центр сферы, по окружностям, перпендикулярным

оси вращения (рис. 91). Эти окружности на одной из проекций вырождаются в прямые линии, а на другой могут изображаться в натуральную величину (рис. 92).

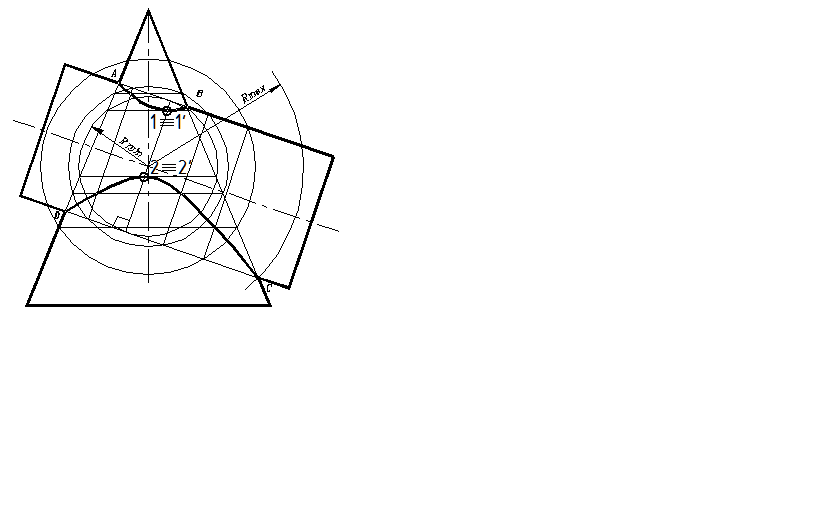
Рассмотрим последовательность построения линии пересечения конуса вращения и цилиндра вращения методом сфер (рис. 97).

1. Анализ: две поверхности вращения, их оси пересекаются и ‖П₂ . Используем метод сфер.

2. Опорные точки A,B,C,D определяем на пересечении главных меридианов.

3. Центр концентрических сфер располагаем в точке пересечения осей.

4. Строим наименьшую сферу, вписывая её в

наибольшую из поверхностей (цилиндр).

5. Изображаем прямыми линиями проекции окружнос-

тей, по которым сфера касается цилин­дра (рис. 93) и

пересекается с конусом (рис. 94) и отмечаем кружками Рис. 91 Рис. 92

двойные точки пересе­чения окружностей, принадлежащие линии пересечения объектов 1,1', 2, 2’ (рис. 95,96).

Рис. 93 Рис. 94 Рис. 95 Рис. 96

Рис. 97

6. Увеличиваем радиус сферы и, выполняя действия по пункту 4, строим промежуточ­ные точки. Наибольшая сфера имеет радиус равный расстоянию от центра сфер до наи­более удалённой опорной точки С.

7. Плавно соединяя полученные точки, имеем двойную линию пересечения объектов, проек­ция которой на чертеже представляет ги­перболу.

Частный случай пересечения поверхностей вращения

Форма линии пересечения и её распо­ложение зависят от соотношения размеров поверхностей. Для сравнения: если наиболь­шей поверхностью, в которую вписывается минимальная сфера, будет конус, то линия пересечения, расположится иначе (рис. 98).

Частный случай: Если обе поверхности вращения описаны вокруг общей для них сферы, то пространствен­ная линия пересечения распадается на две пло­ские кривые – эл­липсы 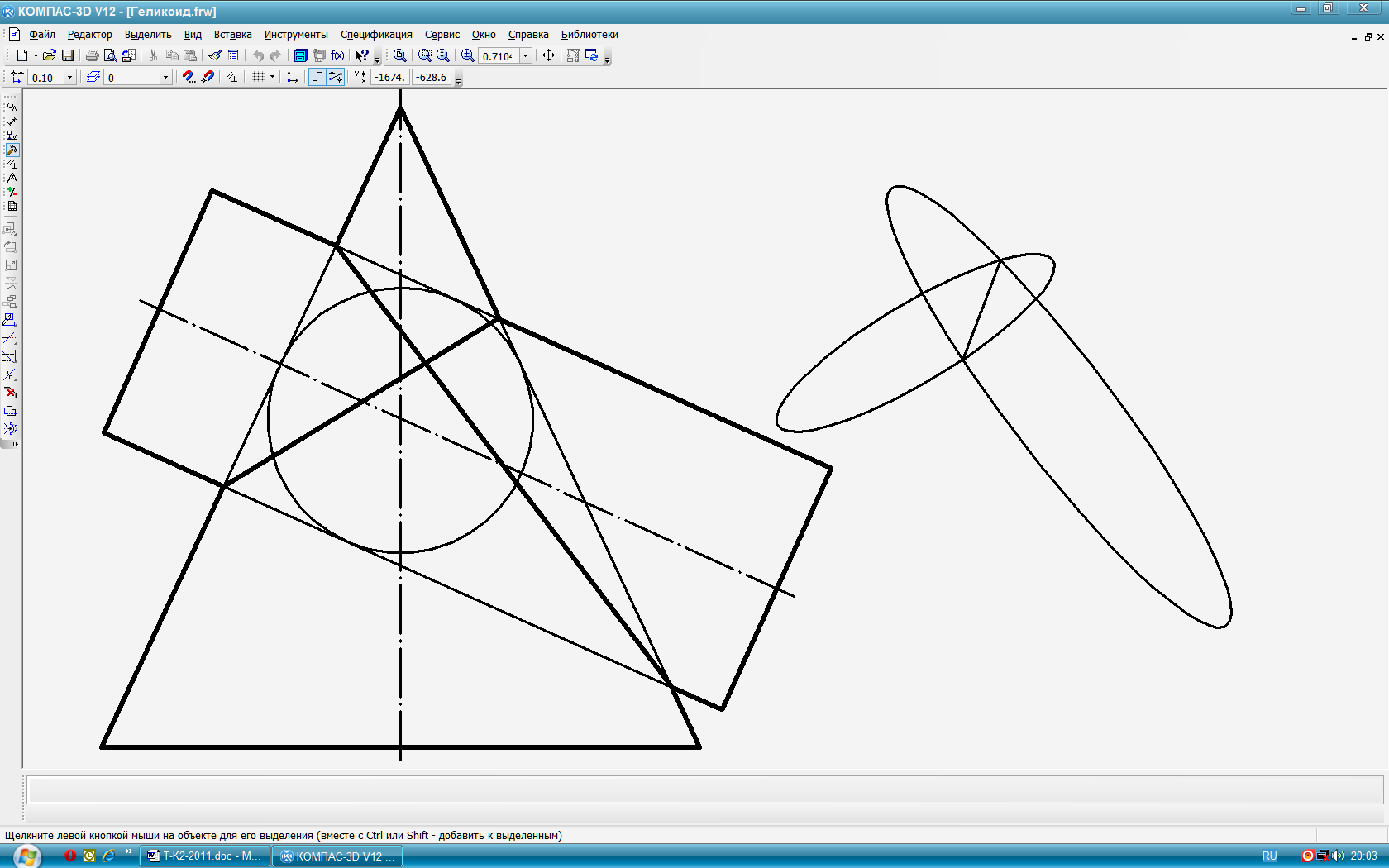(рис. 99).

Рис. 98 Рис. 99

Аксонометрические проекции

применяют для получения наглядных изображений.

Сущность аксонометрического проецирования заключается в том, что задают направление проецирования на объект, не совпадающее ни с одним из его измерений и проецируют его вместе с осями локальной системы координат на одну плоскость, называемую аксонометрической или картинной.

Направление проецирования с аксонометрической плоскостью проекций может составлять прямой или острый углы, что соответствует названиям: прямоугольная или косоугольная аксонометрия. Элементы объекта при аксонометрическом проецировании искажаются. Мерой таких искажений являются коэффициенты искажения, которые всегда меньше единицы. На практике используют приведенные коэффициенты искажения, равные 1 или 0,5 (в зависимости от вида аксонометрии и направления осей). При этом размеры аксонометрических изображений будут несколько больше размеров объекта.

Параллельность, существующая между различными элементами объекта, например, ребрами, ребрами и осями локальной системы координат сохраняется в аксонометрии.

ГОСТ 2.317—69 рекомендует к применению пять видов аксонометрий: две прямоугольные (изометрическую и диметрическую) и три косоугольных (фронтальную и горизонтальную изометрические и фронтальную диметрическую).