Позиционные задачи

- это задачи на определение взаимного положения геометрических объектов. Их 3 группы:

1. Задачи на взаимный порядок (размещение объектов в ограниченном пространстве (в ракетах, подводных лодках), определение видимости конкурирующих элементов).

2. Задачи на взаимную принадлежность (точек и линий плоскости или поверхности).

3. Главные позиционные задачи (ГПЗ) – задачи на построение точек пересечения линий с поверхностями или линий пересечения поверхностей.

В зависимости от вида объектов и их положения различают 3 случая ГПЗ.

1-й случай (ГПЗ-1) – оба пересекающихся объекта занимают проецирующее положение (,).

Возможны 2 варианта: ГПЗ-1а – объекты перпендикулярны одной и той же пл. проекций;

ГПЗ-1б - объекты перпендикулярны разным плоскостям проекций;

2-й случай (ГПЗ-2) – один из 2-х пересекающихся объектов занимает проецирующее

положение (,).

3-й случай (ГПЗ-3) – оба пересекающихся объекта не занимают проецирующее положение

(общий случай решения позиционных задач) (,).

Проецирующие объекты

- это объекты, перпендикулярные к одной из плоскостей проекций и одноимённые ей.

Существует 4 вида проецирующих объектов:

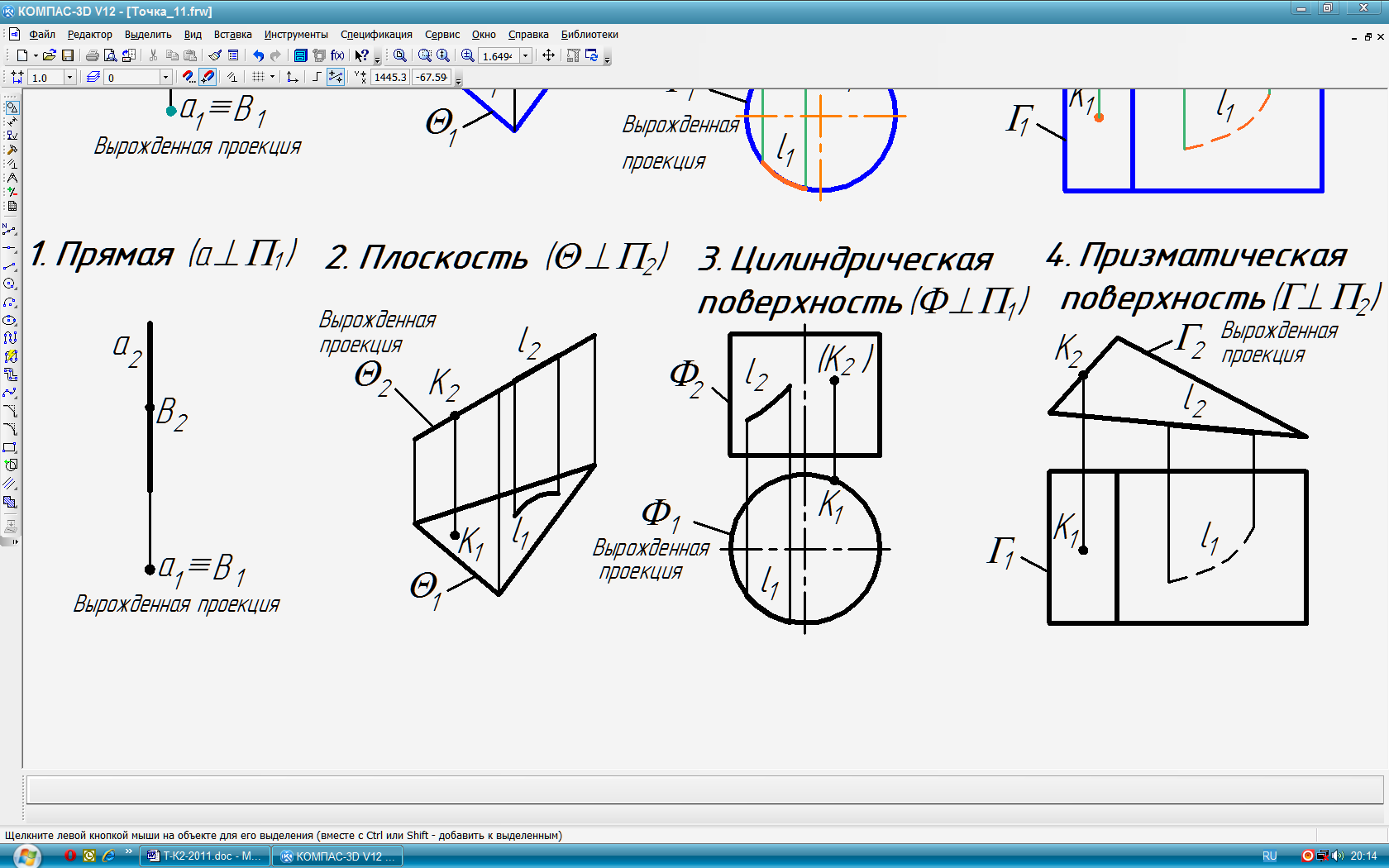
Свойства проецирующих объектов:

1. Одна из проекций этих объектов вырождается в точку или линию.

2. Одна из проекций точек или линий, принадлежащих проецирующему объекту, совпадает с его вырожденной проекцией.

Решение ГПЗ-1, когда оба пересекающихся объекта занимают проецирующее положение

Алгоритм ГПЗ-1а: Если оба объекта перпендикулярны к одной и той же плоскости проекций, то они пересекаются по прямой (прямым), перпендикулярной к этой же плоскости проекций.

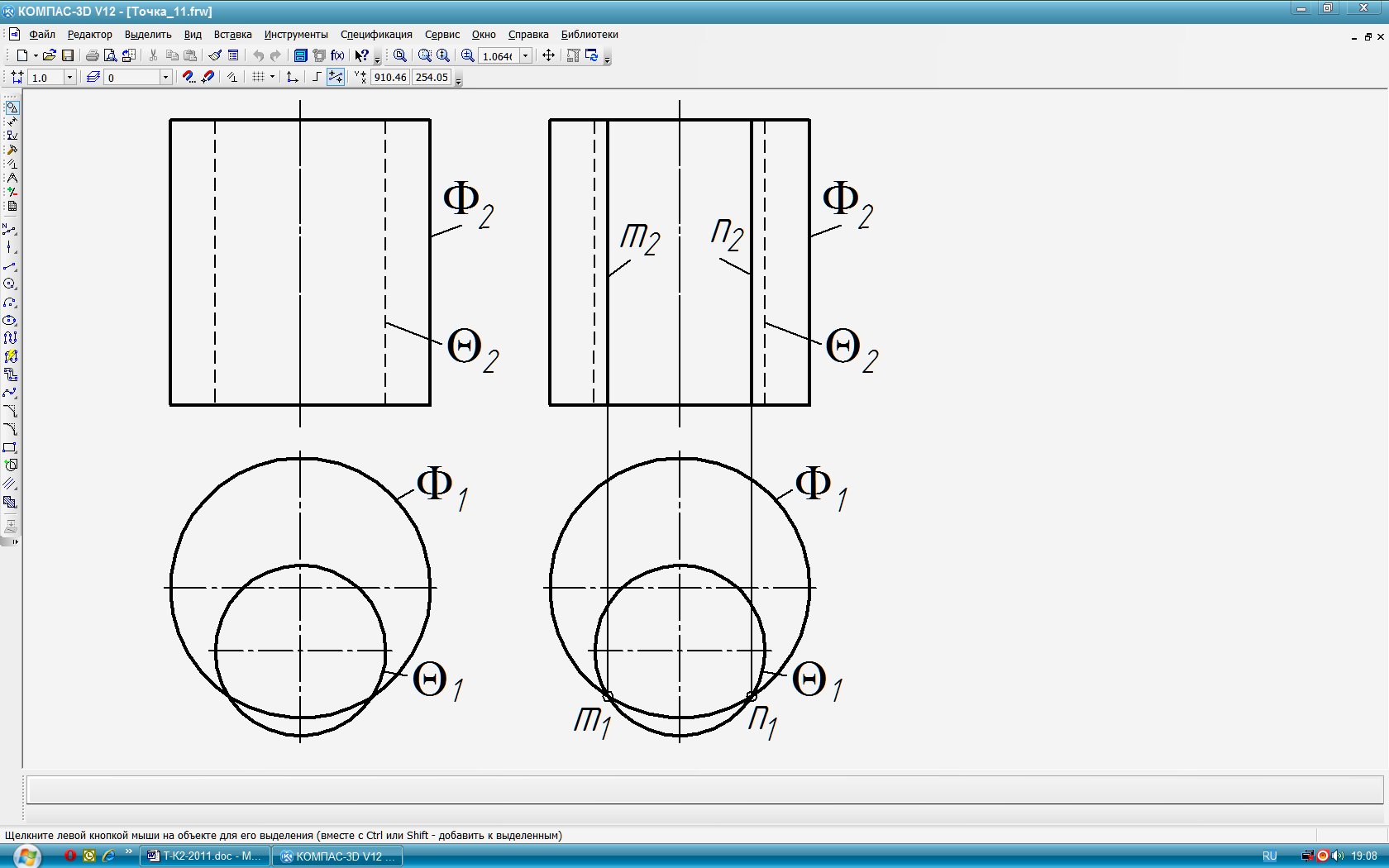
Типовая задача 14 (рис. 81): Построить линии пересечения двух цилиндрических поверхностей.

Кратко запишем условие задачи.

Дано: поверхности  и .

Построить: m,n=∩

Решение (рис. 82)

1. Анализ пересекающихся объектов и их расположение.

П₁ ; П₁  ГПЗ-1а; ₁ и ₁ – вырожденные проекции.

2. Находим на горизонтальной проекции точки пересечения вырожденных проекций поверхностей, которые по алгоритму являются горизонтально-проецирующими прямыми m₁, n₁ = ₁ ∩ ₁ .

m₂, n₂ строим из условия принадлежности поверхностям  и .

Рис. 81 Рис. 82

Алгоритм ГПЗ-1б: Если объекты перпендикулярны к разным плоскостям проекций, то две проекции искомой точки или линии пересечения уже есть на чертеже, т.к. они совпадают с вырожденными проекциями этих объектов (их надо только обозначить). Задача сводится к построению третьей проекции точки или линии пересечения (если необходимо).

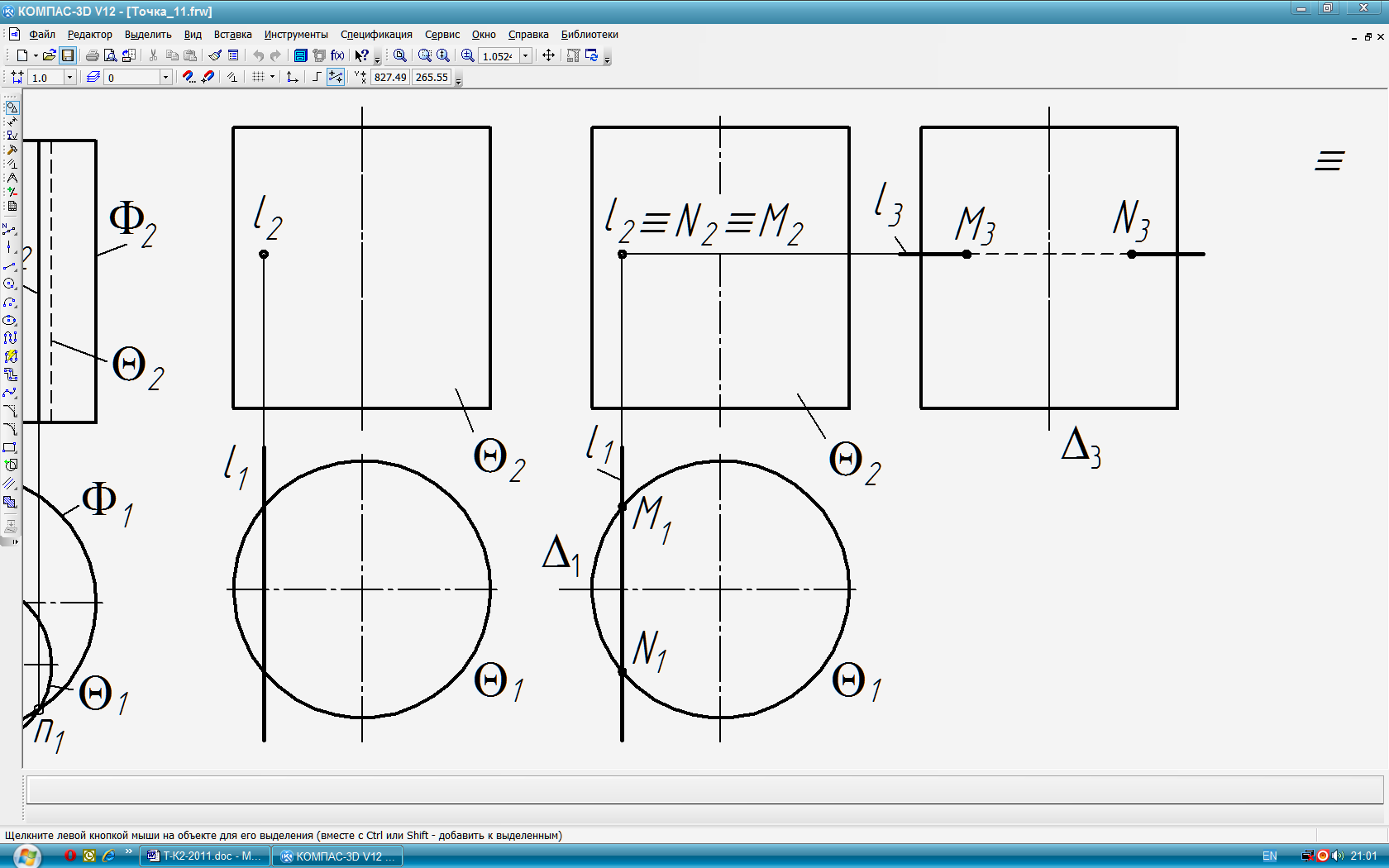
Типовая задача 15 (рис. 83): Построить точки пересечения фронтально-проецирующей прямой с горизонтально-проецирующим цилиндром на трёхкартинном чертеже.

Рис. 83

Кратко запишем условие задачи. Дано: поверхность  и прямая l. Построить: M,N=l∩ Решение (рис. 84) 1. Анализ пересекающихся объектов и их расположение. П1; lП2  ГПЗ-1б; 1 и l 2 – вырож­денные проекции объектов. 2. По алгоритму: M1,N1 = 1∩ l 1; M2,N2 = l 2 . 3. Для построения профильных проекций точек вво­дим базовую плоскость (1,3)‖П2 . Измеряя удаления то­чек M1 и N1 от 1 на горизонтальной проекции и отклады­вая их от 3 на профильной проекции, получим M3 и N3. 4.Определяем видимость прямой методом конкурирующих точек (на прямой и поверхности).

Рис. 84