- •Руководство к выполнению упражнений и заданий по начертательной геометрии
- •Ростов-на-дону
- •Введение
- •Литература
- •Основы начертательной геометрии
- •Основоположник начертательной геометрии
- •Основные понятия
- •Символы математической логики:
- •Требования, предъявляемые к чертежу
- •Получение изображений на плоскости
- •МетоДы проецирования (рис. 2)
- •Выбор направления проецирования на объект или ориентация объекта относительно плоскостей проекций
- •Комплексный чертЁж
- •Образование комплексного чертежа
- •Комплексный чертёж точки (рис. 4,5) Свойства ортогонального проецирования:
- •Построение точек на комплексном чертеже по координатам (рис. 6)
- •Взаимное расположение точек
- •Конкурирующие точки
- •Рекомендации по решению задач
- •Все задачи решать в два этапа:
- •Уметь выполнять типовые действия (построения), которые встречаются практически в каждой задаче по начертательной геометрии:
- •Свойства ортогонального проецирования (продолжение):
- •Относительное положение прямых Свойства ортогонального проецирования (продолжение):
- •Комплексный чертёж плоскости
- •Относительное положение прямой и плоскости, двух плоскостей
- •Многогранники и тела вращения
- •Пирамида
- •Тела вращения (элементарные) цилиндр
- •Преобразование комплексного чертежа
- •Способ замены плоскостей проекций
- •Способ плоскопараллельного перемещения (рис. 40-41)
- •Вращение вокруг проецирующей прямой
- •Разрез ─ ортогональная проекция предмета, мысленно рассечённого полностью или частично одной или несколькими плоскостями для выявления его невидимых поверхностей.
- •Поверхности
- •Поверхности линейчатые неразвёртываемые
- •Поверхности вращения
- •Позиционные задачи
- •Проецирующие объекты
- •Решение гпз-2, когда один из 2-х пересекающихся объектов занимает проецирующее положение
- •(Общий случай решения позиционных задач)
- •Метод вспомогательных секущих плоскостей
- •Метод вспомогательных секущих сфер
- •Частный случай пересечения поверхностей вращения
- •Аксонометрические проекции
- •Прямоугольная аксонометрия
- •Косоугольная аксонометрия
- •Алгоритм построения аксонометрической проекции
- •Развёртывание поверхностей
- •Графоаналитический способ построения разверток цилиндрических, конических поверхностей [4]
- •Приближённый и условный способы построения разверток поверхностей
- •Введение……………………………………………………………………………………………………………………………………………………………………………………………………………………………..……3 литература……………………………………………………………………………………………………………………………………………………………………………………………………………………..………3
- •Тела вращения (элементарные) ……………………………………………………………………………………………………………………………………………………………………………………21
- •Конус………………………………………………………………………………………………………………………………………………………………………………………………………………………….………22 преобразование комплексного чертежа…………………………………………………………………………………………………………………………………………………………………23
- •Позиционные задачи…………………………………………………………………………………………………………….………………………………………………………………………………………….37
- •Аксонометрические проекции………………………………………………………………..……………………………………………………………………………………………………….……………42
Поверхности линейчатые неразвёртываемые
Поверхности с плоскостью параллелизма (Каталана): цилиндроиды, коноиды, косая плоскость.
Рис. 60
Рис. 62 |
Эти поверхности образуются при перемещении прямой линии l, во всех своих положениях сохраняющей параллельность некоторой заданной плоскости (плоскости параллелизма), и пересекающей две направляющие скрещивающиеся линии m и n. Получаемая поверхность с плоскостью параллелизма определяется конфигурацией двух направляющих скрещивающихся линий. Если они обе (m и n) кривые линии, то образующаяся поверхность - цилиндроид (рис 60), если одна из них кривая, а другая прямая, то – коноид (рис 61), а если обе направляющие – прямые линии, то – косая плоскость или гиперболический параболоид (рис. 62). Коноид, у которого одна направляющая - винтовая линия (гелиса) m, а вторая направляющая – её ось g, называется винтовым. Другое название этой винтовой поверхности – прямой геликоид (рис 63). |
Рис. 61
Рис. 63 |
Поверхности вращения
Рис. 64
Рис. 66
Рис. 70
Рис. 72
Рис. 74 |
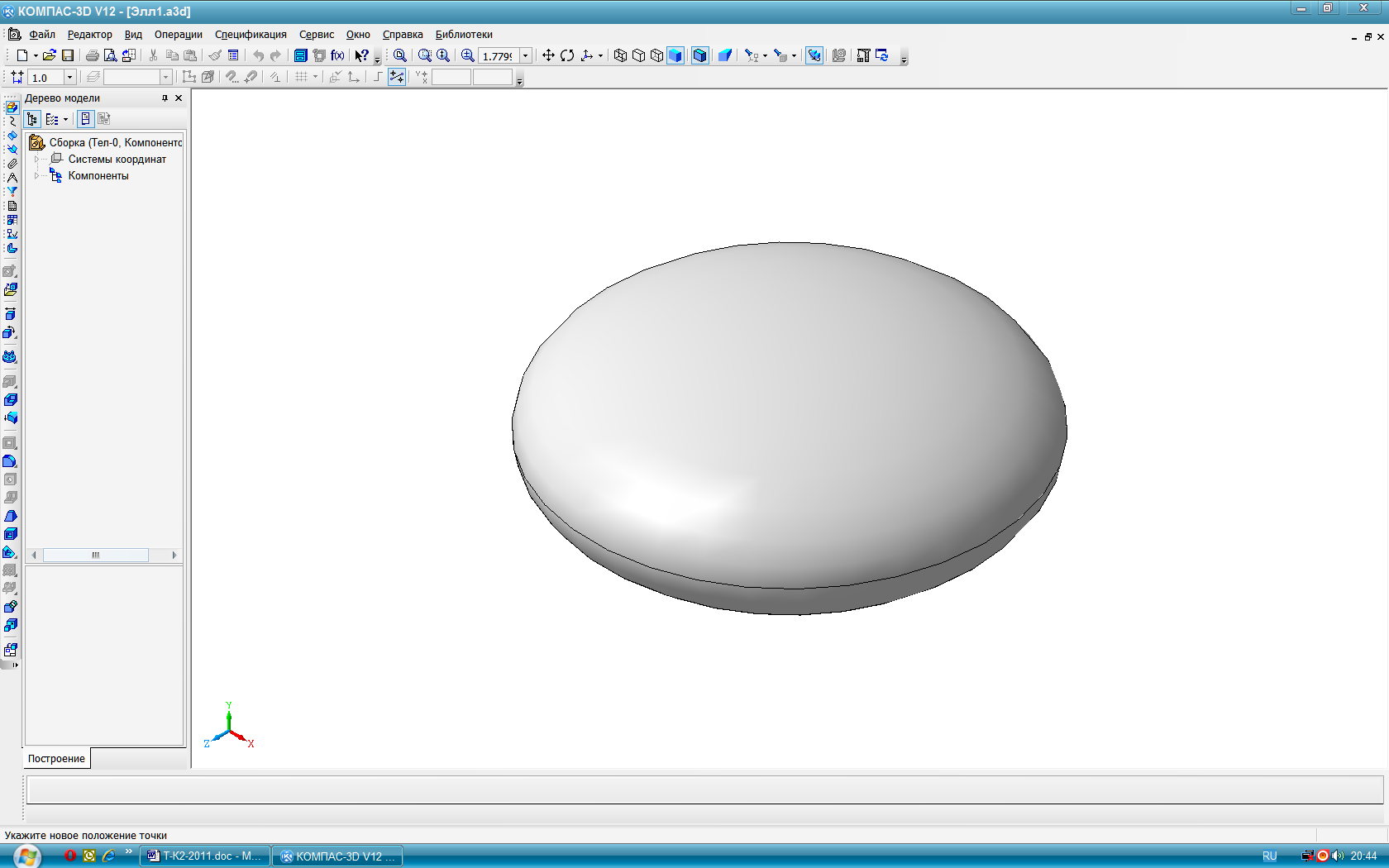
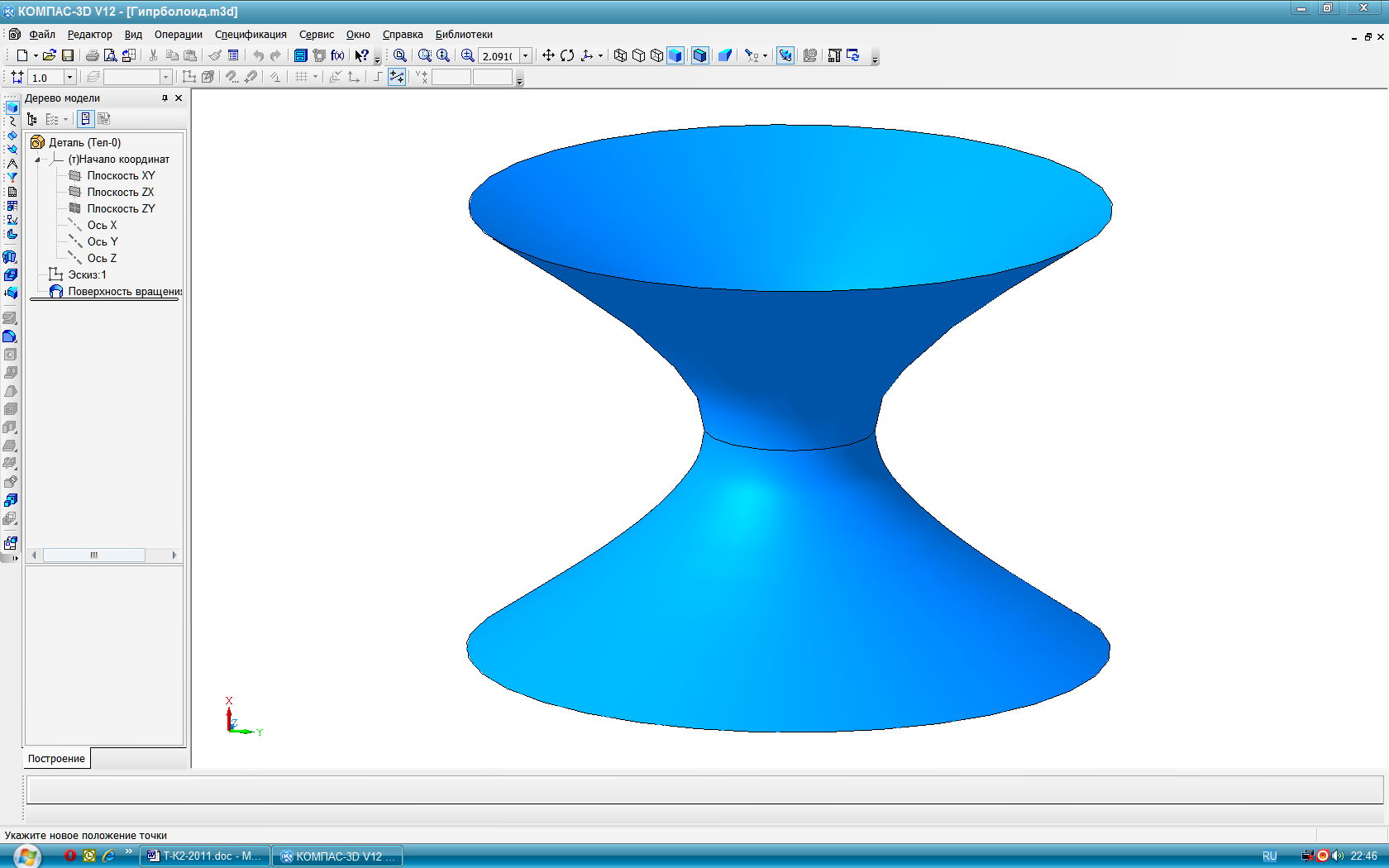
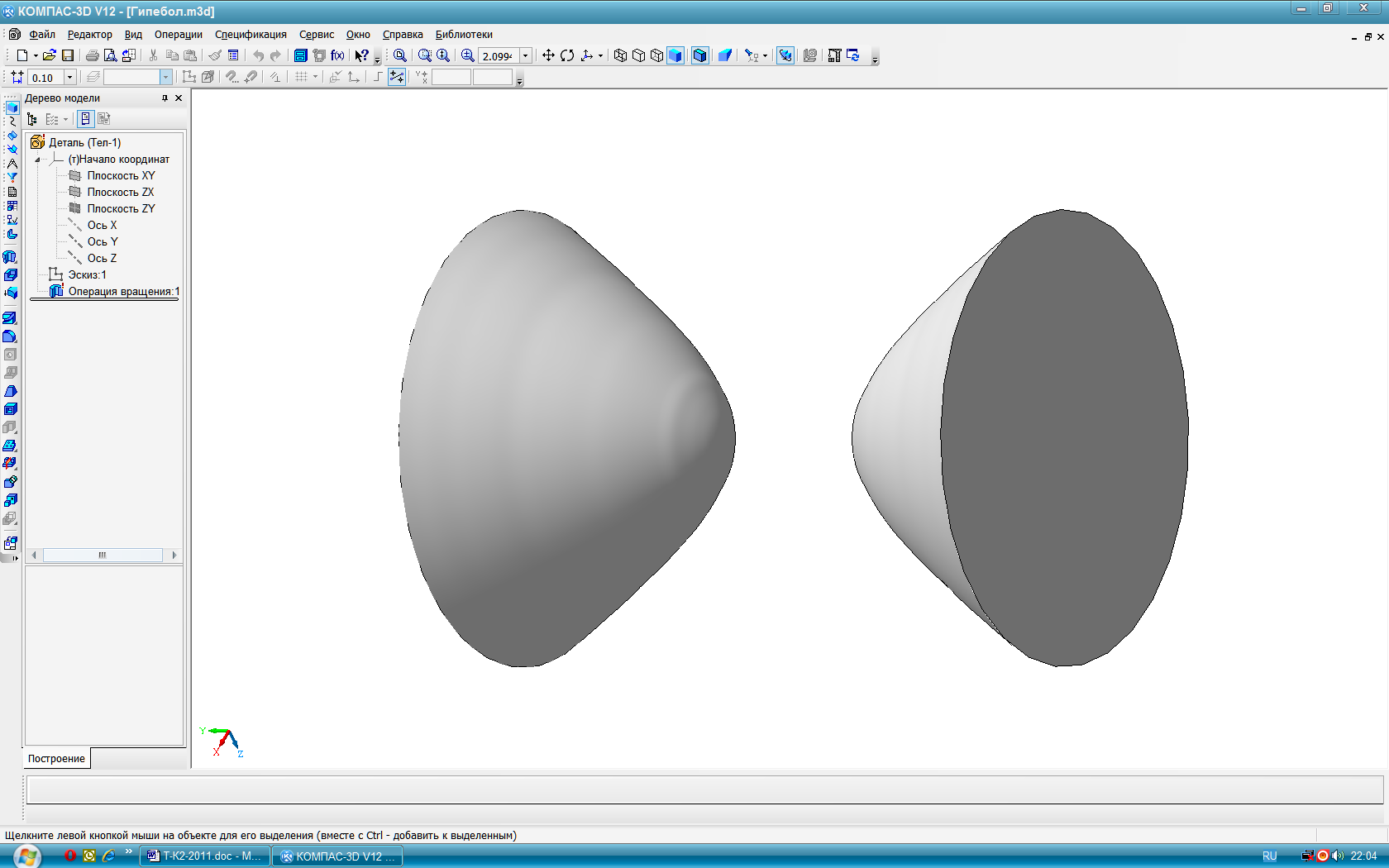
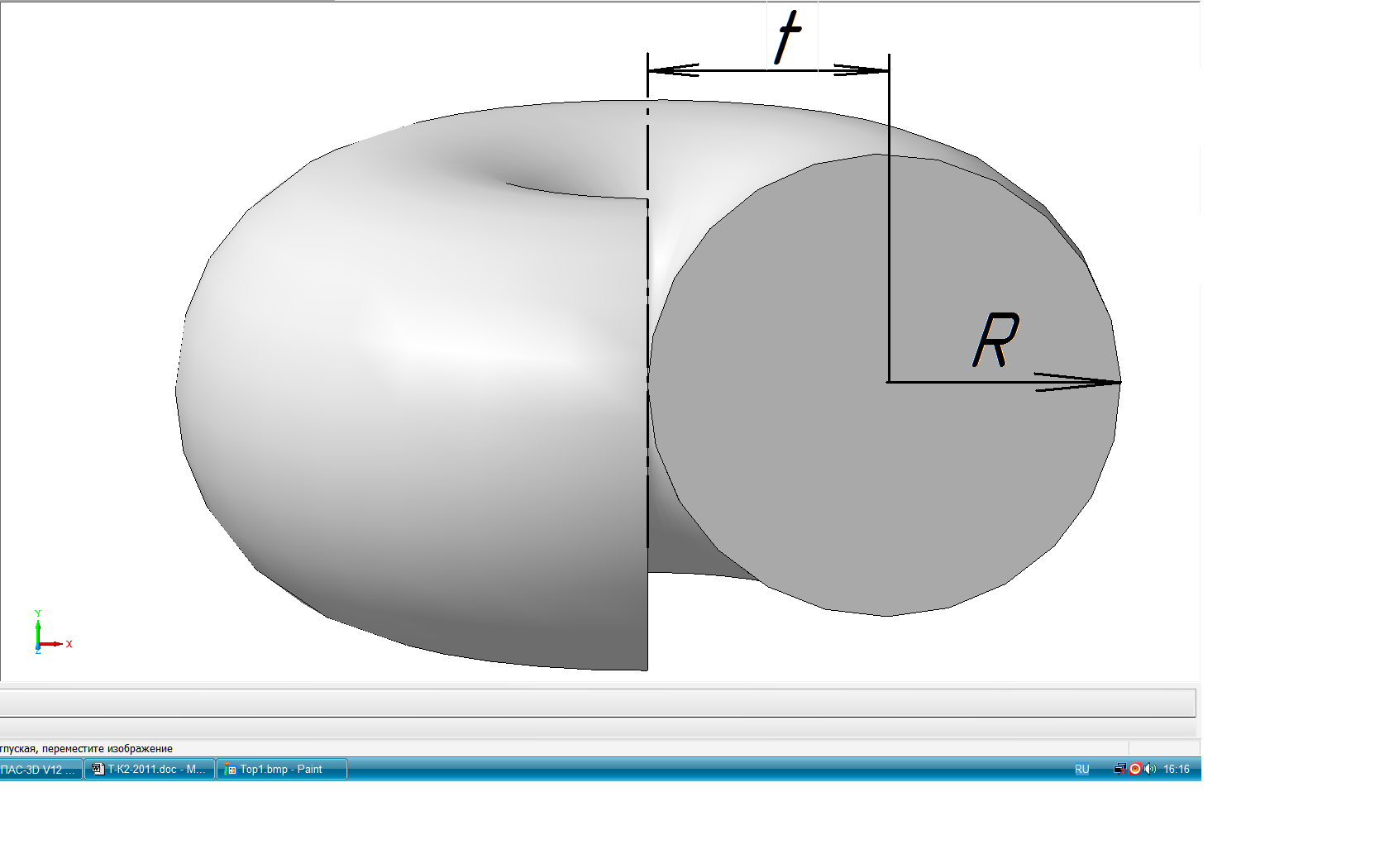
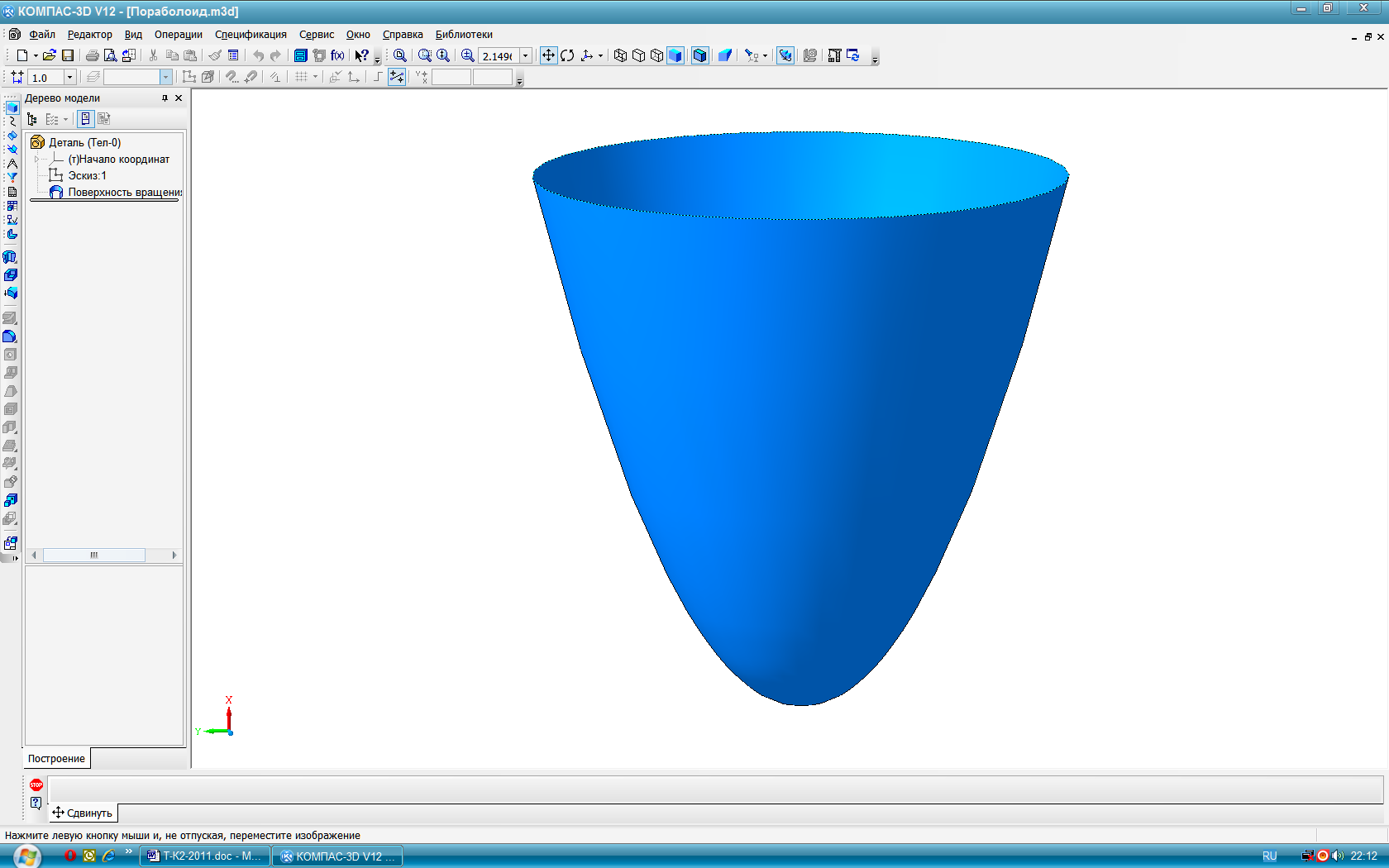
образуются в общем случае вращением некоторой образующей l вокруг оси g (рис. 64). Все точки образующей описывают в пространстве окружности с центром на оси вращения – параллели. Наибольшая и наименьшая параллель называются соответственно экватор и горло. Плоскости, проходящие через ось поверхности вращения, называются меридиональными, а линии, по которым они пересекают поверхность – меридианами. Меридиональная плоскость, параллельная плоскости проекций, даёт в сечении главный меридиан. Прямолинейная образующая l, в зависимости от её положения относительно оси вращения g, может образовывать линейчатые поверхности: 1) цилиндрическую если l∥g (рис. 65); 2) коническую если l∩g (рис.66); 3) однополостного гиперболоида если l∸g (рис. 67). Эта поверхность может быть также образована вращением гиперболы вокруг мнимой оси g. Эта поверхность, в отличии от цилиндрической и конической, - неразвёртываемая. В качестве криволинейных образующих для получения поверхностей вращения часто используют кривые 2-го порядка: окружность, эллипс, параболу, гиперболу и др. Окружность и её части, в зависимости от расположения оси вращения, образуют следующие поверхности: Тор открытый (кольцо) при R<t (рис. 68). Тор закрытый замкнутый при R=t (рис.69). Тор закрытый самопересекающийся при R>t (рис. 70). Сфера при t=0 (рис. 71). Поверхности, образованные вращением кривых 2-го порядка вокруг их осей симметрии: эллипсоид сжатый (рис. 72), эллипсоид вытянутый (рис. 73), гиперболоид однополостный (рис. 74), гиперболоид двуполостный (рис. 75) параболоид (рис. 76).
Р |
Рис. 65
Рис. 67 Р
Рис. 71
Рис. 73
Рис. 76 |
Циклические поверхности
Рис. 77 |
образуются перемещением окружности, центр которой перемещается по заданной направляющей линии. Если образующая окружность постоянного радиуса, то формируются трубчатые циклические поверхности (рис. 77), если окружности переменного радиуса, то – каналовые циклические поверхности (рис. 78). |
Рис. 78 |
Топографические поверхности
- поверхности не подчиняющиеся какому-либо геометрическому закону. Это поверхности земной коры, корпуса судов, обшивка самолётов, автомобилей. Они задаются на чертежах с помощью простого каркаса (географическая карта) или сетчатого каркаса (корпуса судов). |
||
Р |
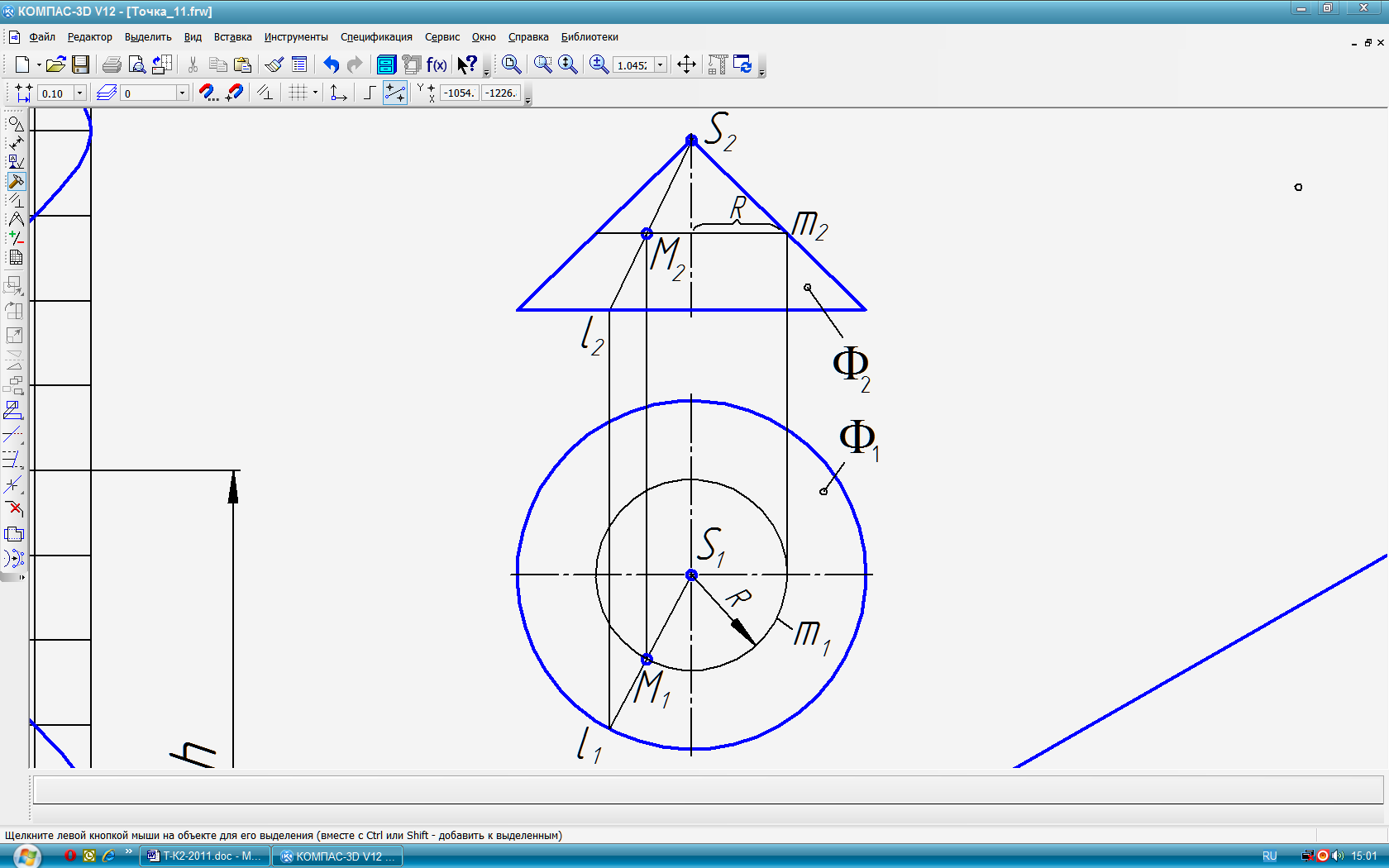
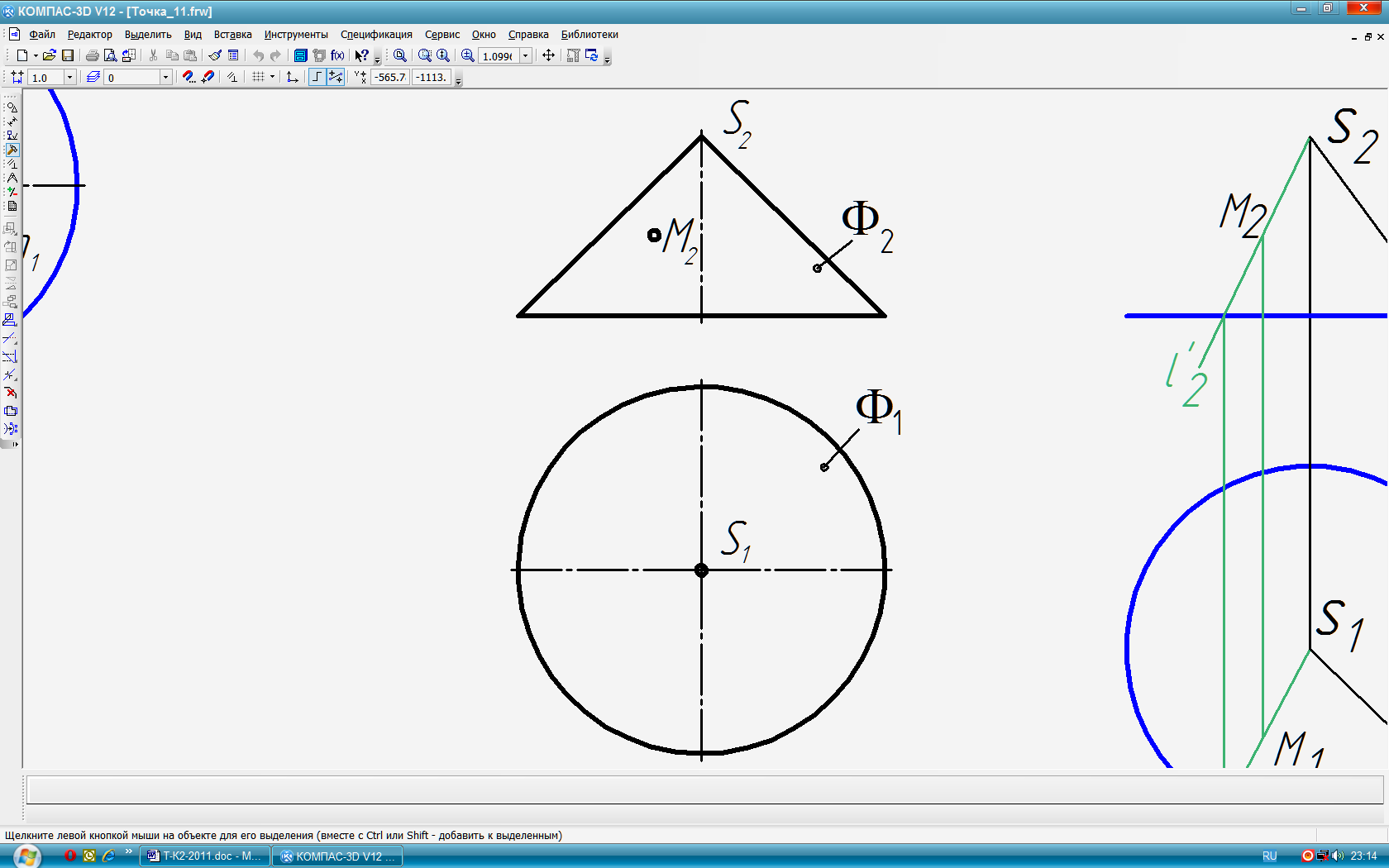
Типовая задача 13 (рис. 79): По заданной проекции точки М(М2 )Î построить её другую проекцию — М1. Используется признак: Точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности. Алгоритм: 1) Анализ поверхности; 2) Через заданную проекцию точки провести вспомогательную для построения линию (образующую, направляющую (окружность для тел вращения)); 3) Построить другую проекцию вспомогательной линии; 4) Проведя линию связи через заданную проекцию точки до пересечения с проекцией вспомогательной линии, найти искомую проекцию точки. Алгоритм подходит для построения точек на всех поверхностях, в том числе и на плоскости. |
Рис. 80 |
Решение (рис. 80 ): 1) Поверхность Ф является конической вращения. Для привязки заданной точки к поверхности используем образующую или окружность; 2) Проводим через точку М2 образующую l2 или окружность m2. 3) Строим горизонтальную проекцию образующей l1 или окружности m1. 4) От точки М2 , проведя вертикальную линию связи до пересечения с горизонтальной проекцией образующей или окружности, получаем горизонтальную проекцию точки М1 Как видно из рис. 80, оба решения совпали.

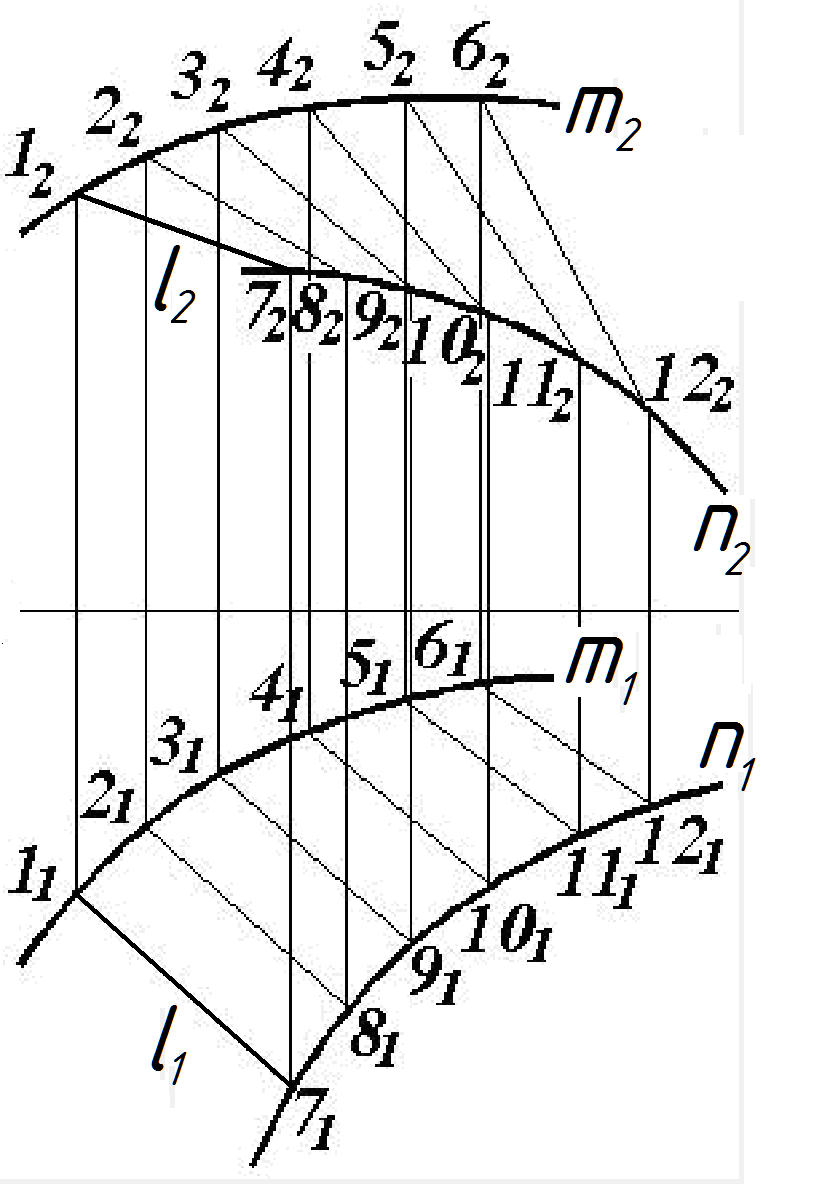
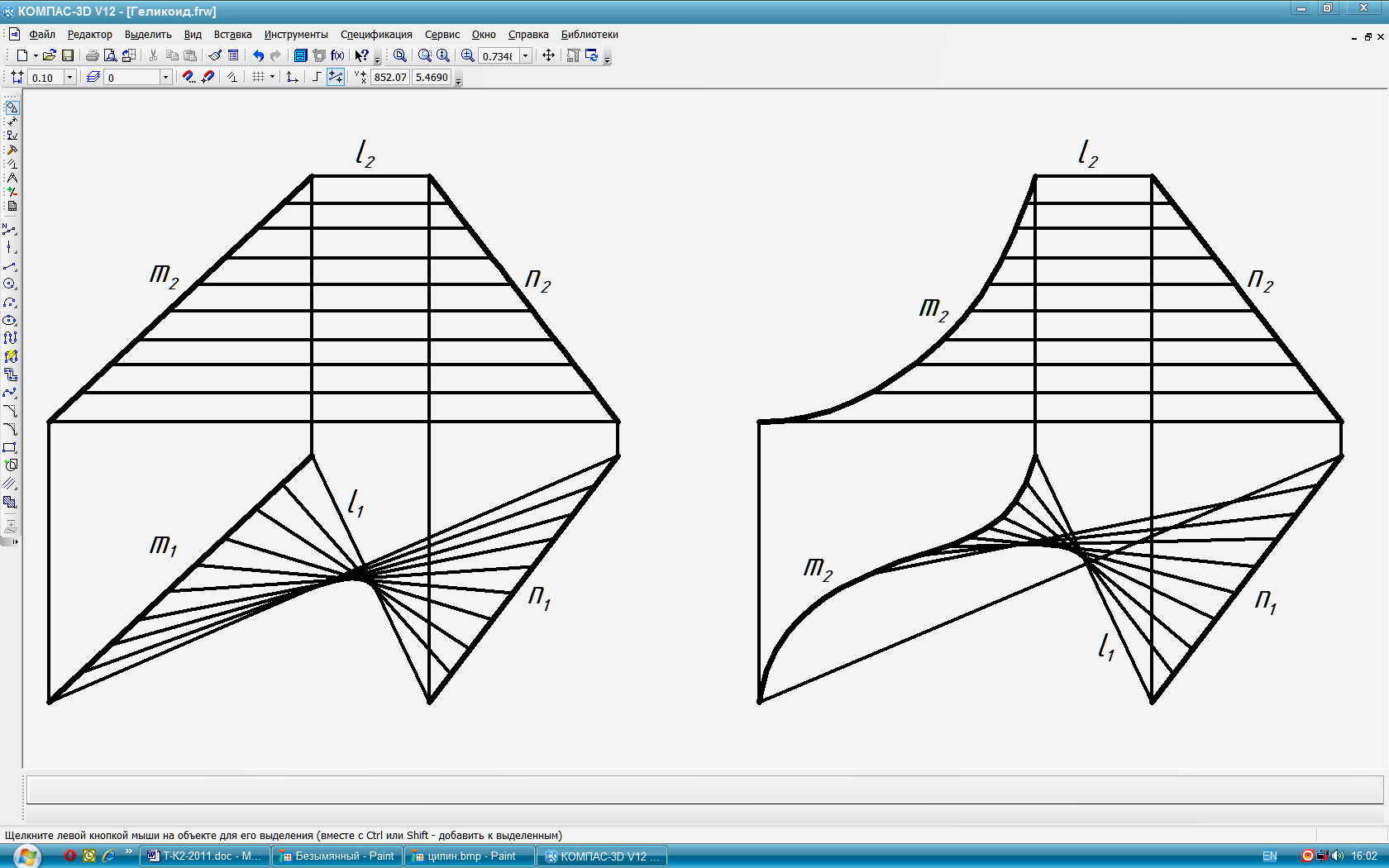
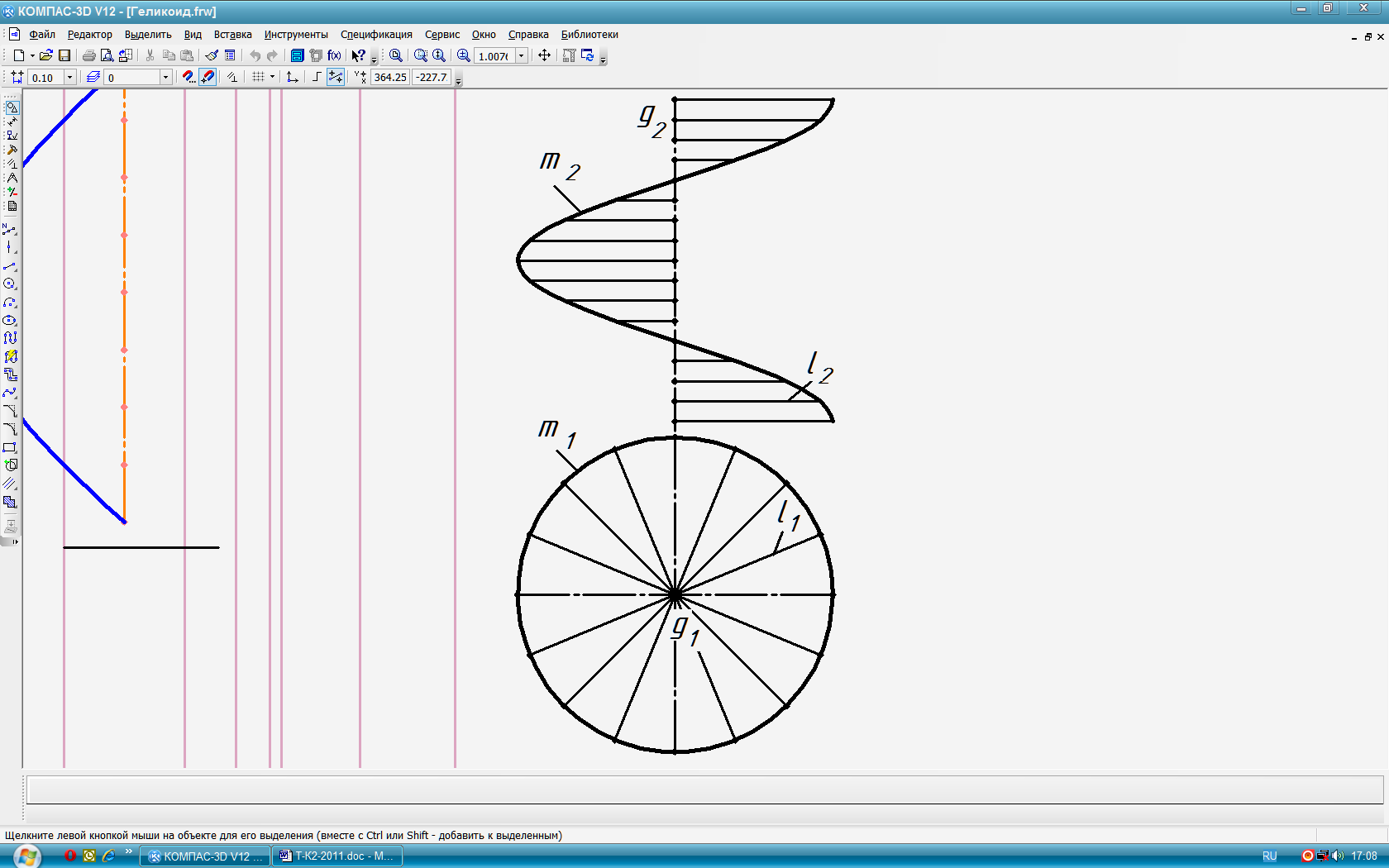

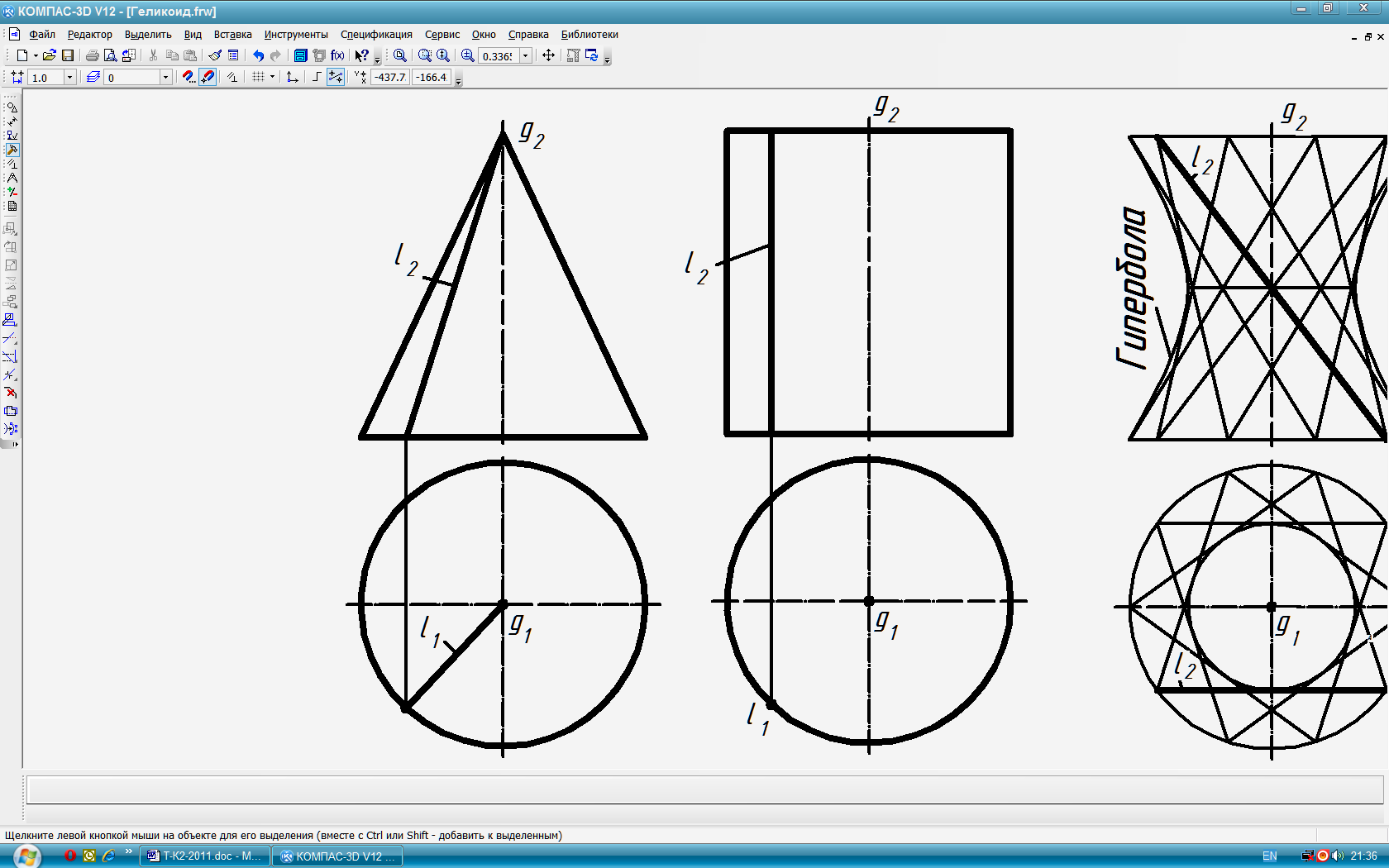
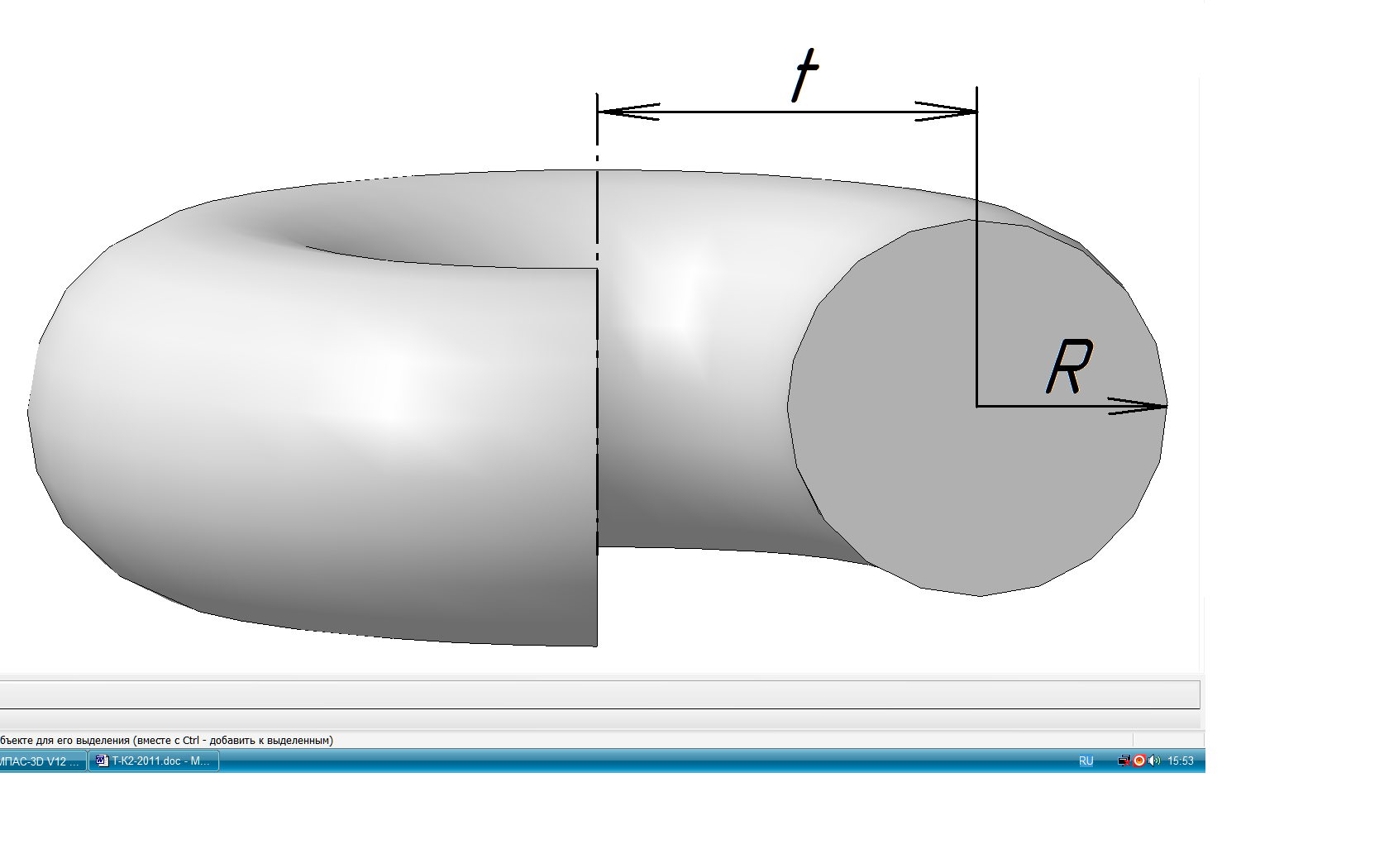 Рис.
68
Рис.
68
 ис.
75
ис.
75
 ис.
69
ис.
69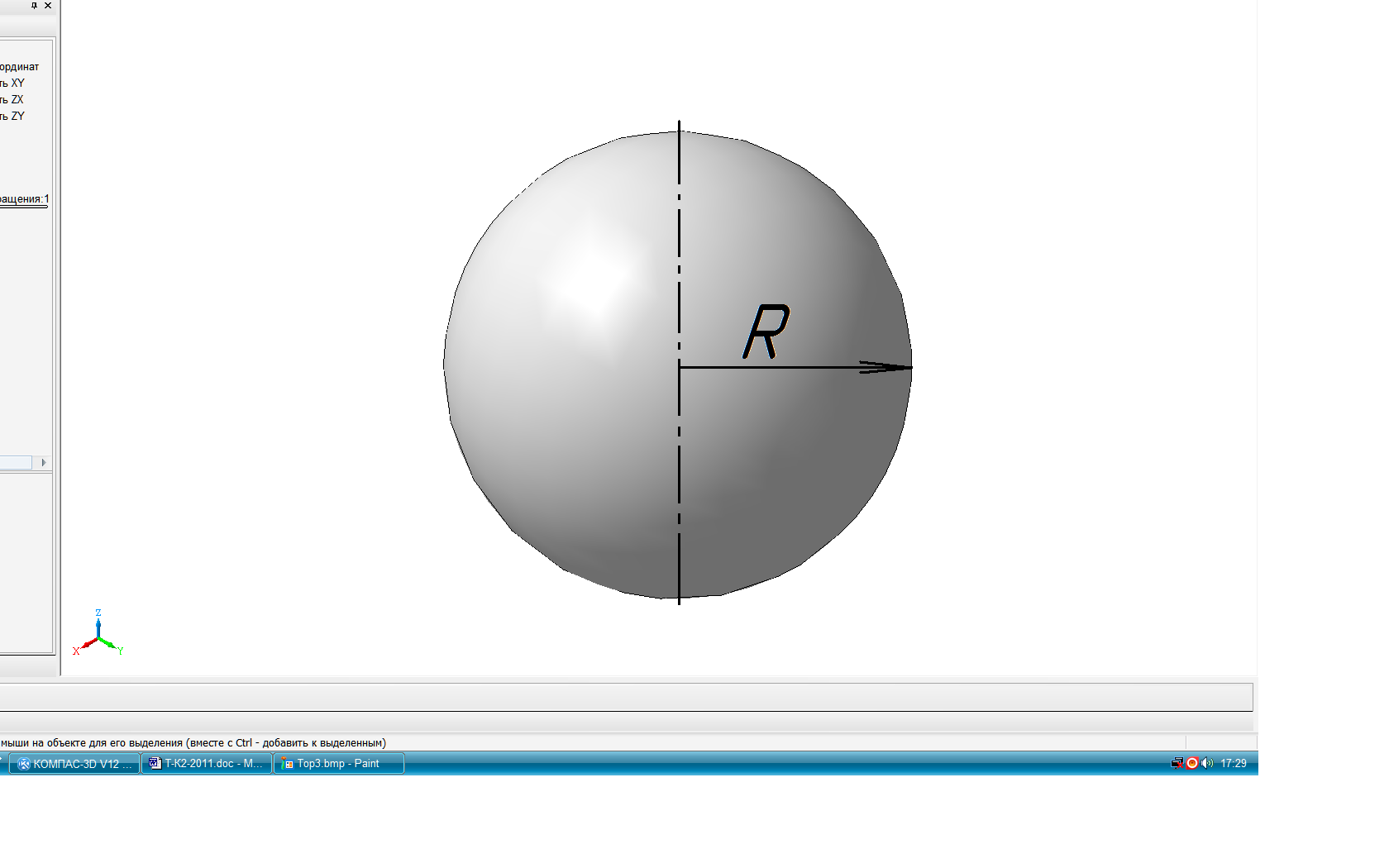

 ис.
79
ис.
79