- •Руководство к выполнению упражнений и заданий по начертательной геометрии
- •Ростов-на-дону
- •Введение
- •Литература
- •Основы начертательной геометрии
- •Основоположник начертательной геометрии
- •Основные понятия
- •Символы математической логики:
- •Требования, предъявляемые к чертежу
- •Получение изображений на плоскости
- •МетоДы проецирования (рис. 2)
- •Выбор направления проецирования на объект или ориентация объекта относительно плоскостей проекций
- •Комплексный чертЁж
- •Образование комплексного чертежа
- •Комплексный чертёж точки (рис. 4,5) Свойства ортогонального проецирования:
- •Построение точек на комплексном чертеже по координатам (рис. 6)
- •Взаимное расположение точек
- •Конкурирующие точки
- •Рекомендации по решению задач
- •Все задачи решать в два этапа:
- •Уметь выполнять типовые действия (построения), которые встречаются практически в каждой задаче по начертательной геометрии:
- •Свойства ортогонального проецирования (продолжение):
- •Относительное положение прямых Свойства ортогонального проецирования (продолжение):
- •Комплексный чертёж плоскости
- •Относительное положение прямой и плоскости, двух плоскостей
- •Многогранники и тела вращения
- •Пирамида
- •Тела вращения (элементарные) цилиндр
- •Преобразование комплексного чертежа
- •Способ замены плоскостей проекций
- •Способ плоскопараллельного перемещения (рис. 40-41)
- •Вращение вокруг проецирующей прямой
- •Разрез ─ ортогональная проекция предмета, мысленно рассечённого полностью или частично одной или несколькими плоскостями для выявления его невидимых поверхностей.
- •Поверхности
- •Поверхности линейчатые неразвёртываемые
- •Поверхности вращения
- •Позиционные задачи
- •Проецирующие объекты
- •Решение гпз-2, когда один из 2-х пересекающихся объектов занимает проецирующее положение
- •(Общий случай решения позиционных задач)
- •Метод вспомогательных секущих плоскостей
- •Метод вспомогательных секущих сфер
- •Частный случай пересечения поверхностей вращения
- •Аксонометрические проекции
- •Прямоугольная аксонометрия
- •Косоугольная аксонометрия
- •Алгоритм построения аксонометрической проекции
- •Развёртывание поверхностей
- •Графоаналитический способ построения разверток цилиндрических, конических поверхностей [4]
- •Приближённый и условный способы построения разверток поверхностей
- •Введение……………………………………………………………………………………………………………………………………………………………………………………………………………………………..……3 литература……………………………………………………………………………………………………………………………………………………………………………………………………………………..………3
- •Тела вращения (элементарные) ……………………………………………………………………………………………………………………………………………………………………………………21
- •Конус………………………………………………………………………………………………………………………………………………………………………………………………………………………….………22 преобразование комплексного чертежа…………………………………………………………………………………………………………………………………………………………………23
- •Позиционные задачи…………………………………………………………………………………………………………….………………………………………………………………………………………….37
- •Аксонометрические проекции………………………………………………………………..……………………………………………………………………………………………………….……………42
Поверхности

Поверхность - это двухпараметрическое множество точек. Поверхность можно представить как общую часть двух смежных пространств. Порядок графической поверхности определяется по числу точек пересечения её прямой линией.
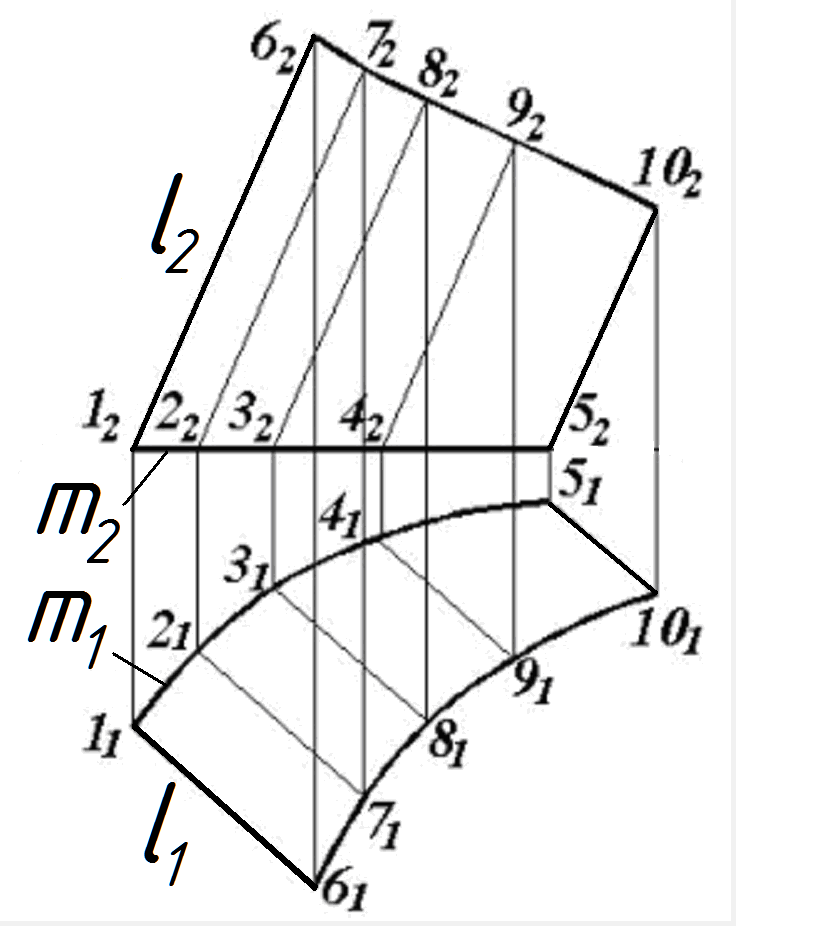
В начертательной геометрии используется кинематический принцип представления поверхности как совокупности всех последовательных положений некоторой перемещающейся в пространстве линии li , называемой образующей (рис. 52). Траектория m, по которой перемещается образующая линия, называется Рис. 52
направляющей линией. Образующие и направляющие линии одной поверхности можно менять местами. В качестве направляющей линии часто задают линию, по которой данная поверхность пересекает пл. П1 .
Способы задания поверхностей на чертеже
Поверхность на комплексном чертеже может быть задана: определителем поверхности, каркасом, условными проекциями. Поверхность считается заданной, если по известной проекции точки, принадлежащей данной поверхности, можно построить вторую её проекцию.
Определитель поверхности – задаваемая совокупность независимых условий, однозначно определяющих поверхность. Определитель состоит из двух частей: геометрической и алгоритмической. В геометрическую часть входит совокупность геометрических фигур.
В алгоритмическую часть — сведения о характере образующей и законе образования поверхности. Первую часть заключают в круглые скобки, вторую — в квадратные. Например: определитель конической поверхности вращения имеет вид (рис. 53):
 (l,
g,
S);
[li
∩g=S,
li
↺g],
где: S
-
вершина конуса, l
-
образующая, g
-
ось конуса.
(l,
g,
S);
[li
∩g=S,
li
↺g],
где: S
-
вершина конуса, l
-
образующая, g
-
ось конуса.
С помощью этого определителя по заданной фронтальной проекции точки М(М2 )Î , построена её горизонтальная проекция М1 . Графическая лаконичность определителя поверхности не отличается наглядностью.
Каркас – упорядоченное множество линий, принадлежащих поверхности. Он может быть простым - состоять из линий одного семейства (рис. 52), или сетчатым – из линий двух семейств (рис. 54). Линии, составляющие каркас, это последовательные положения образующей при её движении по направляющей, а также линии сечения поверхности пучками плоскостей: параллельных или проходящих через ось (для тел вращения). Например, сетчатый каркас конической поверхности вращения составляют два семейства линий (см. рис. 54):
|
|
|
1) li – образующие – прямые, проходящие через вершину S; 2) mi - окружности переменного радиуса с центром на оси конической поверхности. Плотность каркаса определяется дискретами: линейным или угловым у промежутками между смежными линиями каркаса. Каркасный способ отличается хорошей наглядностью, позволяет легко строить недостающие проекции точек, расположенных на его линиях, но достаточно трудоёмок в исполнении.
Рис. 53 Рис. 54 Рис. 55
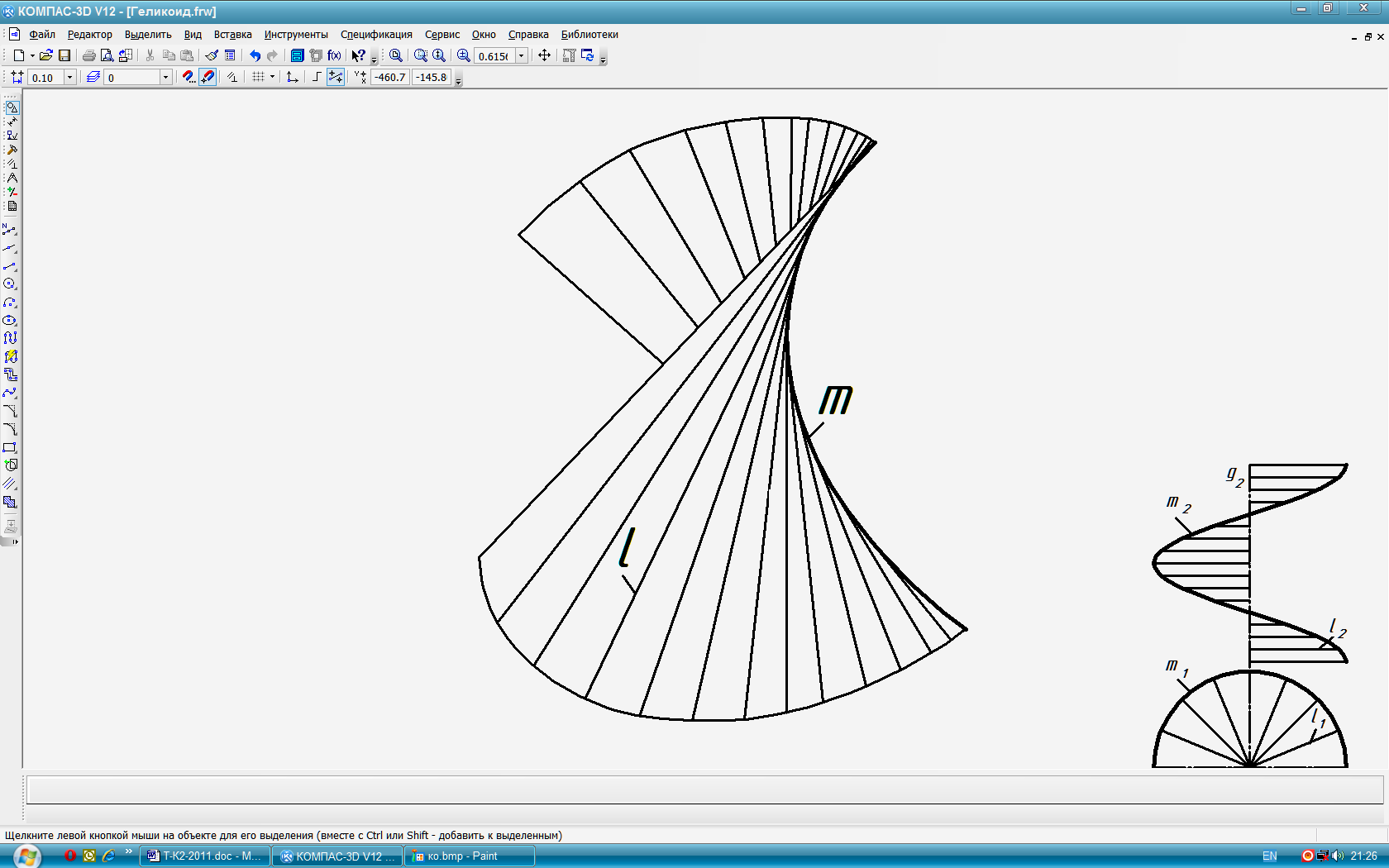
Условные проекции поверхности – проекции очерка отсека (части) поверхности, включающего в себя, кроме проекций линий контура (очертания), также проекции линий обреза (рис. 55). Очертания проекций поверхности изображают с отсечёнными частями, что позволяет увеличить масштаб её изображения и чёткость чертежа. Этот способ, ввиду простоты и наглядности задания поверхностей, применяется наиболее часто (рис. 66).
Поверхности различаются по: форме образующей, закону её движения, признаку развёртываемости, закону изменения формы образующей, закону образования поверхности и др. признакам. Любую поверхность можно получить разными способами. На практике выбирают самый простой.
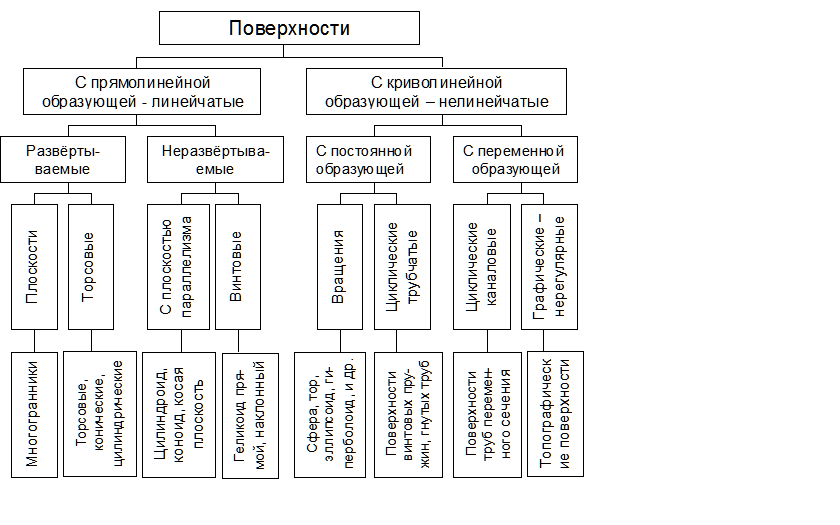
Поверхности линейчатые развертываемые: гранные, цилиндрические, конические, торсовые.
Образующая линия – прямая.
Рис. 56
|
Гранная поверхность - это совокупность плоскостей. Такую поверхность имеют все многогранники. На рис. 56 представлена гранная призматическая поверхность. Цилиндрическая поверхность (рис. 57) образуется параллельным движением прямой линии l, проходящей последовательно через все точки некоторой кривой направляющей линии m. Коническая поверхность (рис. 58) образуется прямой линией l, проходящей последовательно через все точки кривой направляющей линии m и через неподвижную точку, называемой вершиной конической поверхности S. Торс (рис. 59) образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата, которое делит торс на две полости. Коническую и цилиндрическую поверхности можно рассматривать как частные случаи поверхности торса, когда её ребро возврата вырождается в точку (конечную или бесконечно удалённую). |
Рис. 57
Рис. 59 |

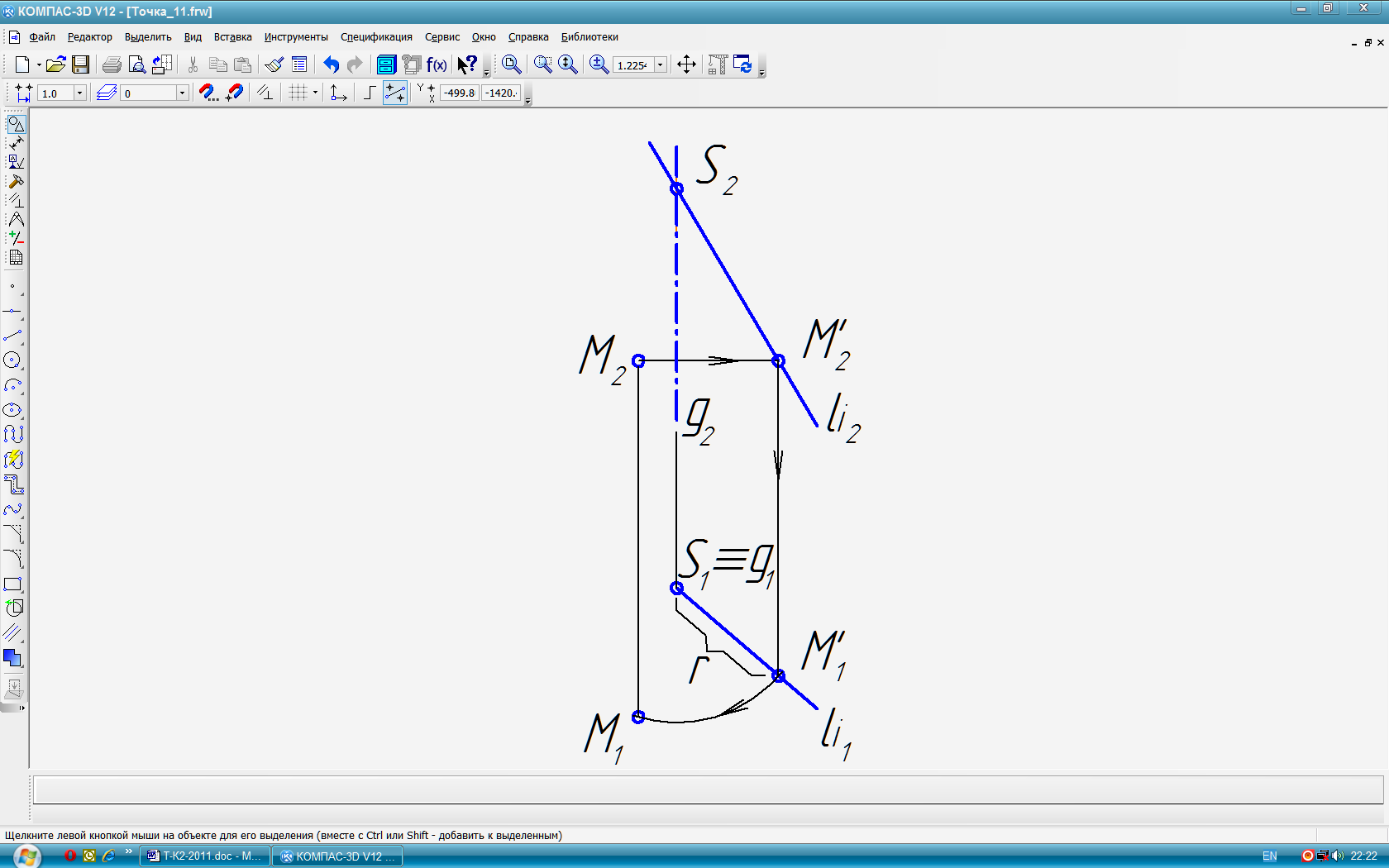
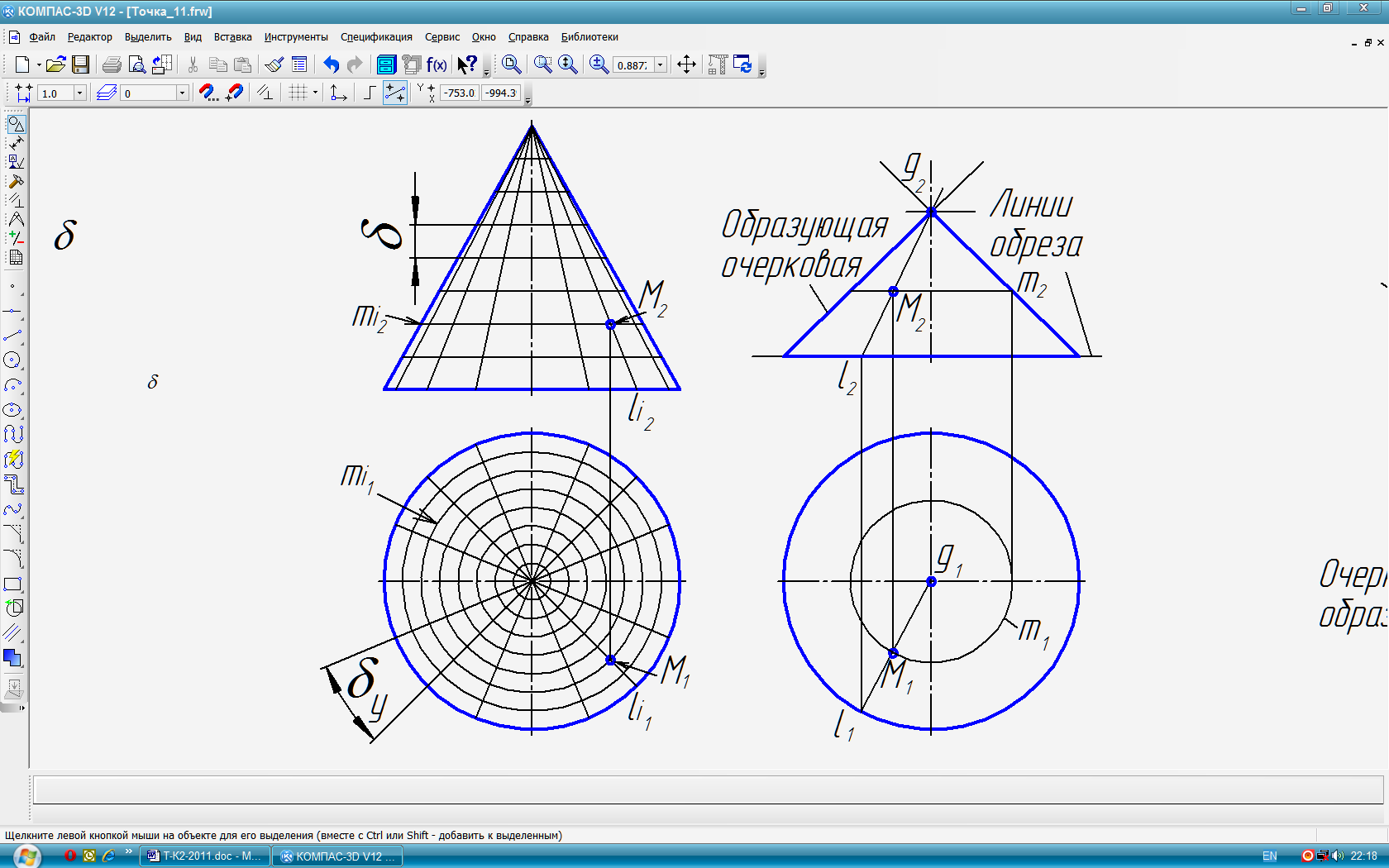
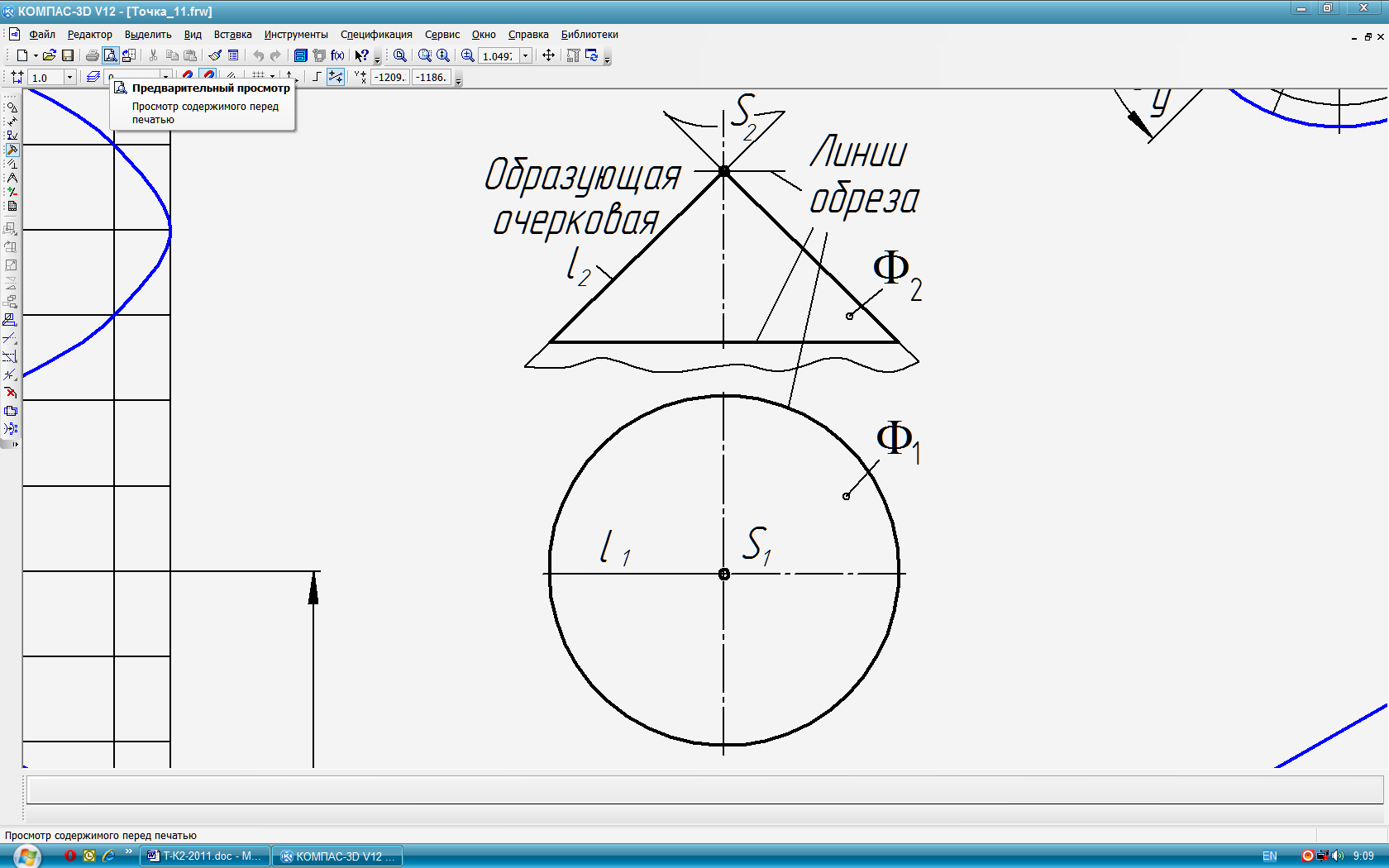
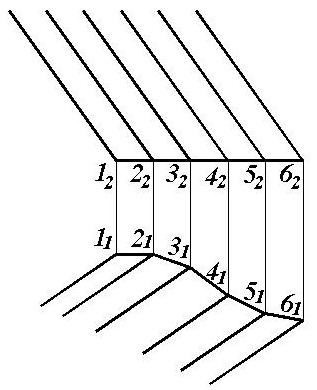
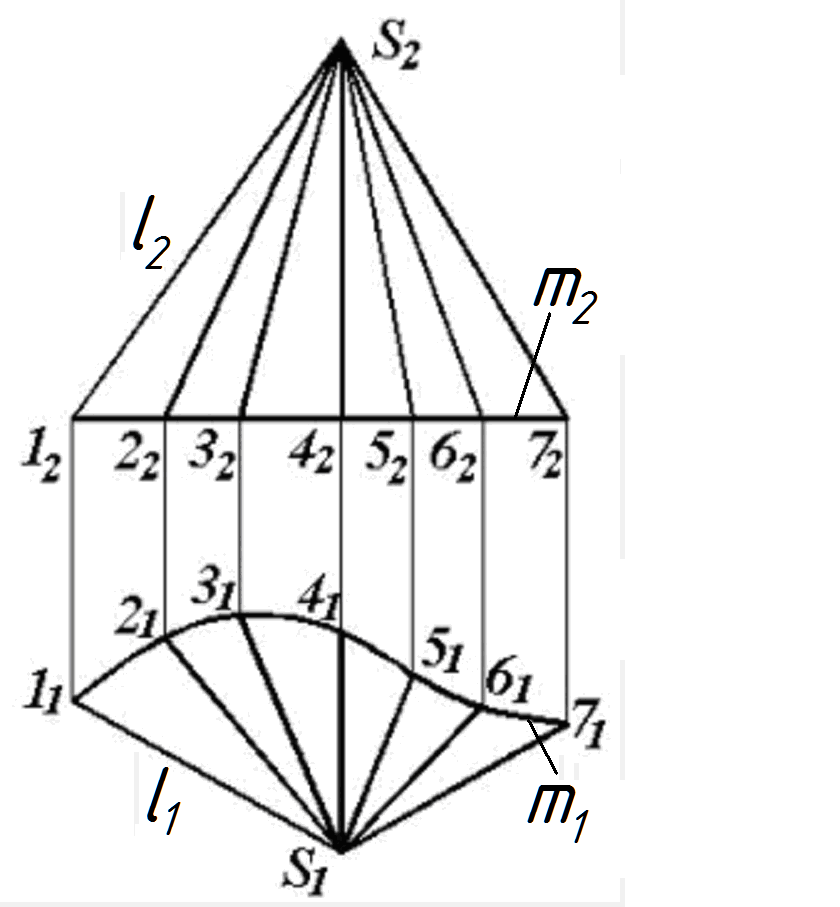 Рис.
58
Рис.
58