Разрез ─ ортогональная проекция предмета, мысленно рассечённого полностью или частично одной или несколькими плоскостями для выявления его невидимых поверхностей.

Ч асть предмета, ближайшую к наблюдателю и не позволяющую видеть внутренние формы объекта, мысленно отбрасывают (рис. 40).

На разрезе показывают то, что находится в секущей плоскости и за ней. Отверстия и полости, попадающие в разрез, становятся видимыми и их контуры изображают сплошной толстой основной линией. Элементы детали, расположенные на её наружной поверхности (ребра, выступы и др.), в разрезе становятся невидимыми. Тело предмета в секущей плоскости штрихуют, а отверстия, полости и рёбра жёсткости (продольно рассечённые), оставляют не за-

Рис. 40 штрихованными. Разрезы, как правило, выполняют в

проекционной связи с другими изображениями пред-

мета, на одном из которых разомкнутой линией показывают вырожденное положение секу

щей плоскости, а стрелками направление взгляда на предмет (рис. 41). Секущая плоскость и

разрез обозначают одной и той же парой заглавных букв кириллицы через тире.

Разрезы размещают на свободном поле чертежа или на месте соответствующих видов, если плоскость сечения параллельна основной плоскости проекций. На рис. 41 фронтальный разрез размещен на месте вида спереди, а профильный (А-А) на месте вида слева. Если секущая плоскость совпадает с плоскостью симметрии предмета, то её и разрез не обозначают (фронтальный разрез на рис. 41). Совмещение вида с разрезом на одном изображении допускается только для симметричных изображений (рис. 42). В качестве разделяющей (вид и разрез) линии принимается осевая линия. Подробно о построении разрезов см. в [14].

Рис. 41 Рис. 42

Для несимметричных изображений, а также в случае, если на осевую линию проецируется контурная, например ребро многогранника, в качестве разделяющей линии используют сплошную волнистую линию таким образом, чтобы эта контурная линия (ребро) была бы видимой (рис. 43). То есть, если ребро находится на наружной поверхности, то дают больше вида, если ребро – на внутренней поверхности, то дают больше разреза.

Классификация разрезов:

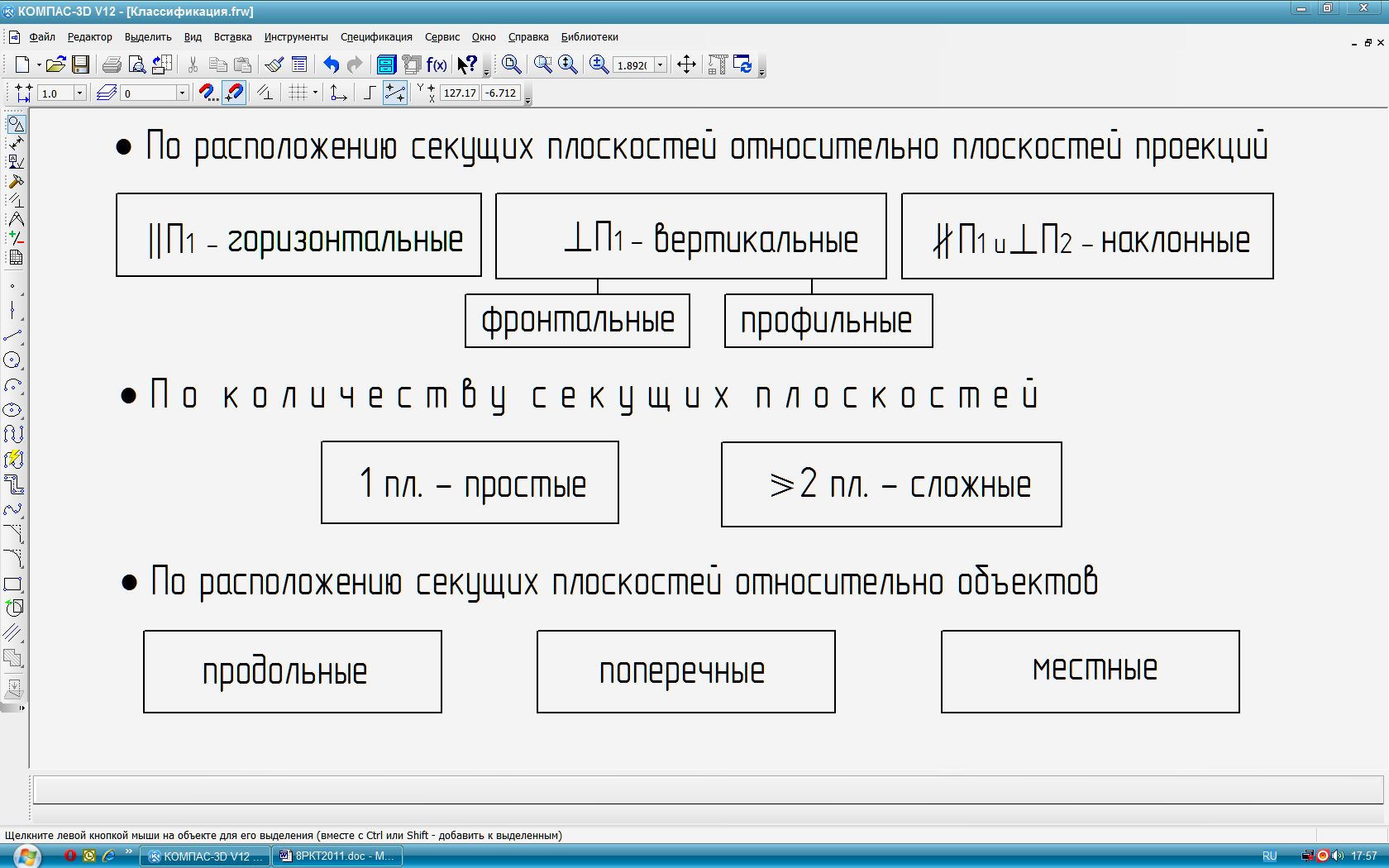
Рис. 43

Т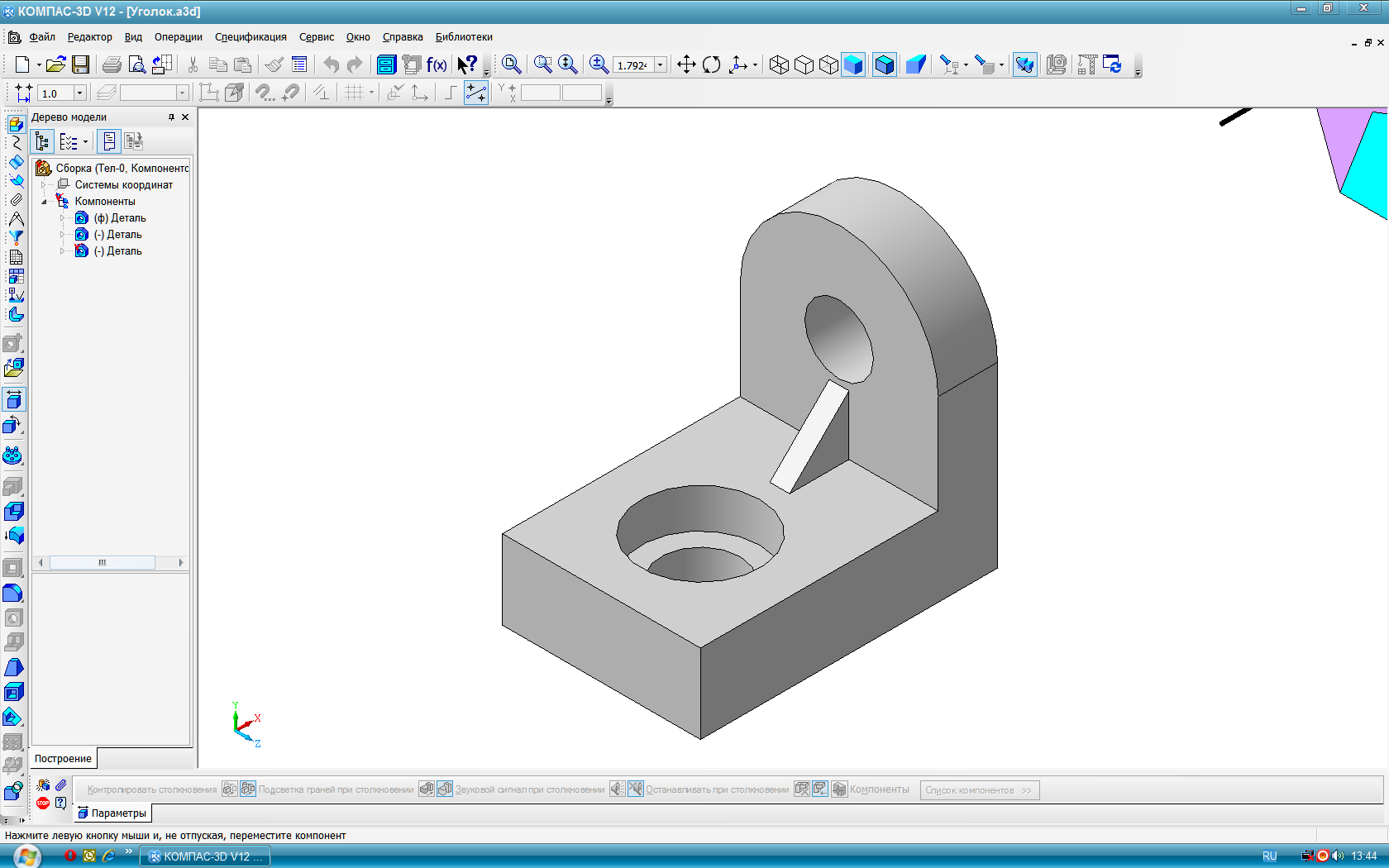 иповая задача 11 (рис. 44-45): Построить гори­зонтальный, фронтальный и профильный разрезы детали (рис. 38), имеющей гладкое и ступенчатое отверстия, а также ребро жёсткости. Рассекаем деталь горизонталь­ной плоскостью уровня А-А, проходящей через ось гладкого отверстия и размещаем горизонтальный разрез на месте вида сверху (рис. 45). Рассекаем деталь профильной плос­костью уровня Б-Б, проходящей через ось ступенчатого от­верстия и размещаем профильный разрез на месте вида слева. Рассекаем деталь фронтальной плоскостью уровня,

Рис. 44 совпадающей с плоскостью симметрии детали (без обо-

значения), получим фронтальный разрез на месте главного вида. Секущая плоскость проходит вдоль ребра жёсткости, поэтому оно не штриху­ется.

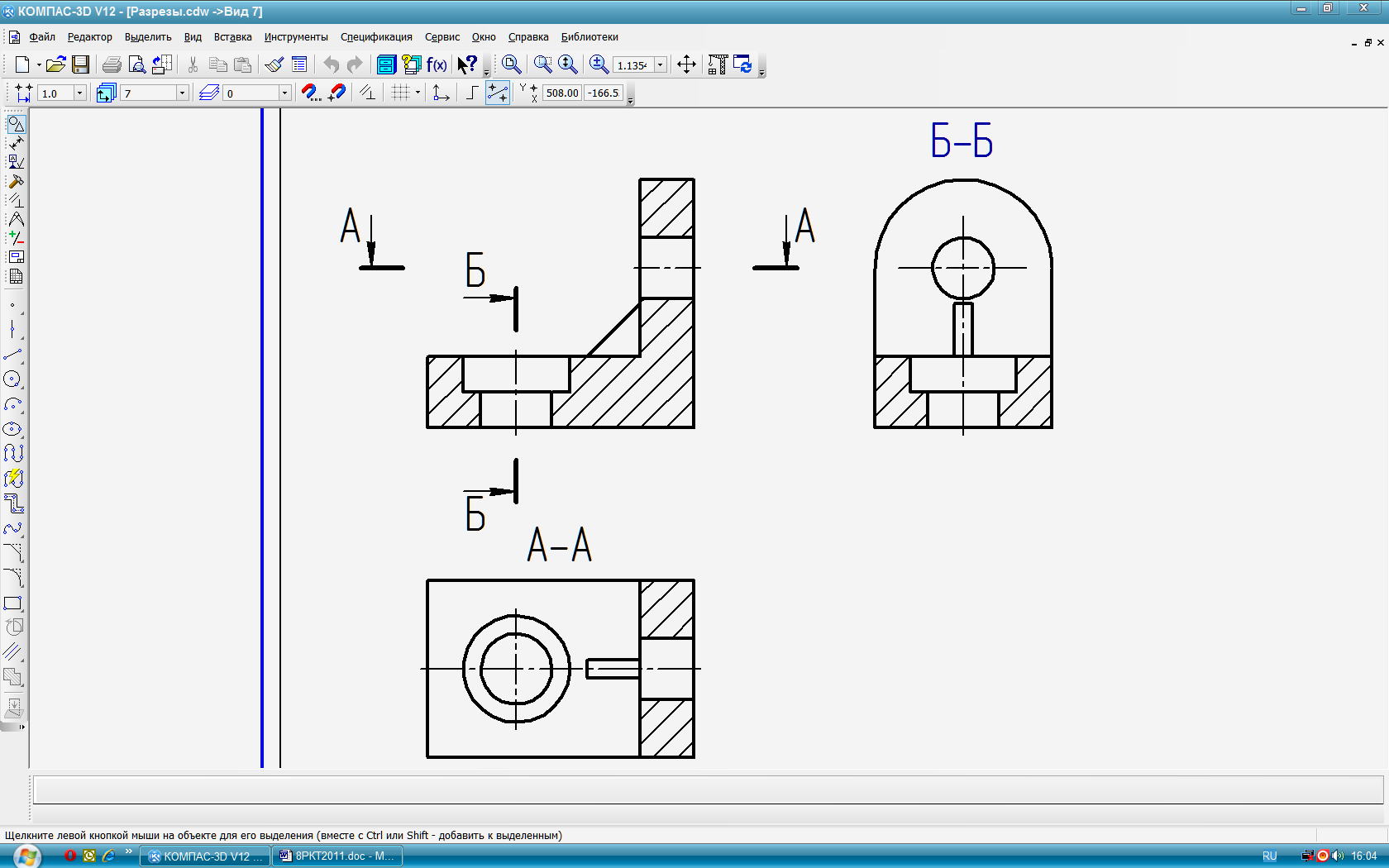Рис. 45

Сечение — это ортогональная проекция фигуры, получающейся в секущей плоскости.

Сечения тел представляют собой плоские фигуры, а сечения поверхностей – линии. В сечении изображается только то, что располагается в секущей плоскости. Сечение – это часть разреза. Для сравнения на рис. 46 изображено сечение, выполненное той же секущей плоскостью А-А, что и разрез на рис. 41. Сечения подразделяются на вынесенные (рис. 46, 47) и наложенные (рис. 48). Контур вынесенного сечения, а также сечения, входящего в состав разреза изображают сплошными основными линиями, а контур наложенного сечения — сплошными тонкими линиями (рис 48). Оформление вынесенных сечений на чертеже такое же, как и разрезов.

.

Рис. 46 Рис. 47 Рис. 48

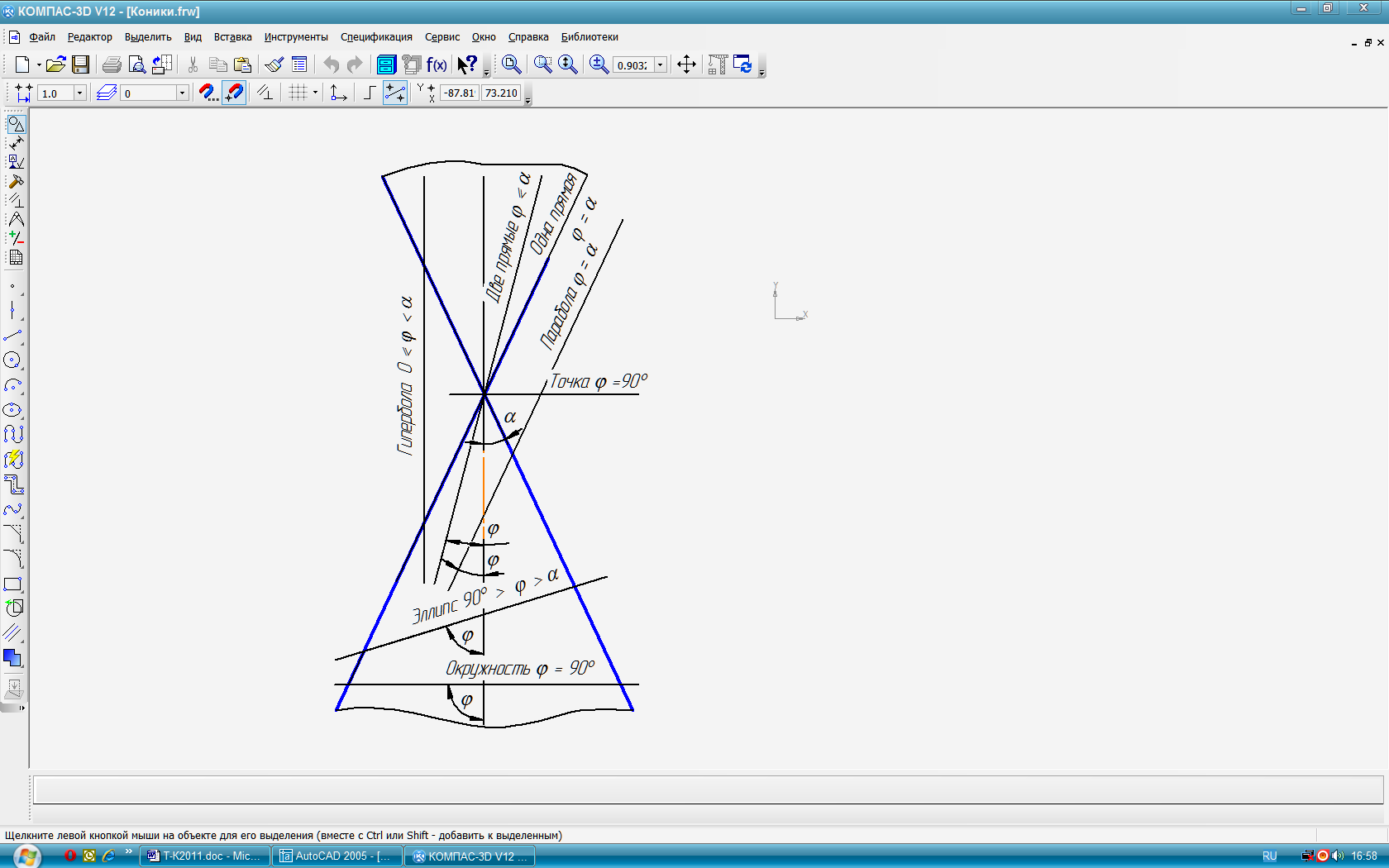Линии конических сечений – это линии, образующиеся при пересечении конуса вращения плоскостями (коники). В зависимости от положения секущей плоскости, угла её наклона к оси конуса  и угла

конуса  линиями сечения могут быть (рис. 49):

окружность – плоскость перпендикулярна оси конуса,

эллипс – плоскость пересекает все образующие и >,

парабола – плоскость параллельна одной из образующих,

гипербола – плоскость параллельна оси конуса,

две пересекающиеся прямые – плоскость проходит через верши-

ну конуса и <,

одна прямая – плоскость касается образующей конуса,

точка - плоскость проходит через вершину конуса и =90.

. Рис. 49 Типовая задача 12 (рис. 50): Постро­ить горизонталь-

ную и профильную проек­ции сечения конуса плоскостью

А-А. Определить натуральную величину сечения.

Рис. 50 Рис. 51

1. По собирательному свойству проецирующей плоскости (см. с. 14) искомая линия сечения совпадает с её фронтальным следом на участке перекрытия его очерком конуса (рис. 51). На вырожденной проекции сечения задаём точки 1₂ ; 2₂ ; 2'₂ ; 3₂ ; 3'₂ ; 4₂ ; 4'₂ . Первая точка одинарная, т. к. лежит на очерковой образующей конуса; остальные - двойные.

2. На поверхности конуса через эти точки проводим окружности r и R, которые на фронтальной плоскости проекций вырождаются в прямые. Строим горизонтальные проекции окружностей. Через заданные проекции точек, проведя вертикальные линии связи до пересечения с окружностями, получим их горизонтальные проекции. Соединив полученные точки, имеем горизонтальную проекцию сечения. Определяем видимость линии сечения.

3. Профильную проекцию сечения строим с помощью базовой плоскости ‖П₂ . Измеряем на горизонтальной проекции удаления точек сечения от базовой линии ₁ (отмечены галочками и крестиками) и откладываем их на профильной плоскости проекций от базовой линии ₃ .

4. Натуральную величину сечения получим, проецируя сечение на дополнительную пл. П₄ , параллельную плоскости сечения и перпендикулярную пл. П₂ . На чертеже задаём базовую линию ₄ параллельную линии сечения А-А, проводим линии связи перпендикулярные базовой линии ₄ и строим дополнительную проекцию сечения на плоскость П₄ точно также, как, например, профильную проекцию. Построение сечений см. также в [14].