Способ плоскопараллельного перемещения (рис. 40-41)

Сущность его заключается в том, что все точки объекта перемещаются в плоскостях уровня по плоским траекториям (на рисунках не показаны). При этом одноимённая плоскостям уровня проекция объекта, меняя своё положение на плоскости, не изменяет своих размеров (рис. 40). Другие проекции точек объекта перемещаются по вырожденным проекциям плоскостей уровня (по прямым).

Алгоритм (рис. 41):

1. Задают на комплексном чертеже частное положение проекции объекта после перемещения.

2. Задают вырожденные проекции плоскостей уровня.

3. Строят дополнительную проекцию объекта.

Типовая задача 9 (рис. 40-41): Преобразовать прямую общего положения АВ в проецирующую прямую. Решается в 2 этапа.

I-й этап: Преобразование прямой АВ общего положения в прямую уровня (фронталь) путём её плоскопараллельного перемещения относительно пл. П₁ .

1 . Перемещаем на комплексном чертеже горизонтальную проекцию А₁В₁ прямой АВ в горизонтальное положение А₁В₁.

2. На фронтальной проекции чертим вырожденные проекции плоскостей уровня _’и _’’ – (проекции траектории перемещения).

3 . Строим дополнительную проекцию прямой А₂В₂ на пересечении вертикальных линий связи с вырожденными проекциями пл. уровня.

II-й этап: Преобразование прямой уровня (фронтали АВ) в проецирующую прямую путём её плоскопараллельного перемещения относительно пл. П₂ .

1 . Перемещаем фронтальную проекцию А₂В₂ в вертикальное положение А₂В₂.

2. На горизонтальной проекции чертим вырожденную проекцию фронтальной проекции пл. уровня _ – (проекцию траектории перемещения).

3 . Строим вторую дополнительную проекцию А₁ В₁ прямой на пересечении вертикальных линий связи с вырожденной пл. уровня.

_{Первое преобразование (I-й этап) применяют, например, для определения натуральной величины отрезка прямой и угла его наклона к пл. проекций, а второе – для определения расстояния между прямой и точкой вне прямой.}

Рис. 40 Рис. 41

Вращение вокруг проецирующей прямой

Этот способ преобразования чертежа является частным случаем плоскопараллельного перемещения (рис. 42). Отличие состоит в том, что точки объекта перемещаются не по произвольным плоским кривым, а по окружностям, центры которых лежат на вводимой оси вращения, перпендикулярной одной из пл. проекций. При вращении объекта вокруг оси одна из его проекций, движется по дугам окружностей с центром в вырожденной проекции оси, а другие проекции объекта движутся по прямым, перпендикулярным к натуральной проекции оси вращения. Алгоритм (рис. 43): 1. Задают на чертеже ось вращения i(i1 , i2), занимающую проецирующее положение. 2. Задают положение объекта после вращения. 3. Строят дополнительную проекцию объекта. Типовая задача 9 (рис. 42-43): Методом вращения вокруг проецирующей прямой определить натуральную величину отрезка прямой АВ и угол её наклона к пл. П1 . 1. Задаём на комплексном чертеже ось вращения i  В, i(i1,i2) П1. 2 . Вращаем горизонтальную проекцию прямой А1В1 вокруг вырожденной проекции оси i1 до положения А1В1 параллельного пл. П2 . 3 . Через (∙)А2 проводим прямую, перпендикулярную оси i2 и на пересечении с вертикальной линией связи от (∙)А1 находим её фронтальную проекцию после вращения - А2 На дополнительной проекции В2 А2 прямая АВ и угол её наклона  к пл. П1 изображаются в натуральную величину.

Рис. 42 Рис. 43 СТАНДАРТЫ ЕСКД (Курс Черчения) Теоретической базой черчения является начертательная геометрия. Однако, су­ществует разница в терминологии. Если изображения объекта в начертательной геомет­рии, чаще всего, именуются проекциями, то в черчении принята более тонкая их диффе­ренциация. На схеме представлена классификация изображений в зависимости от их со­держания.

Вид – ортогональная проекция обращённой к наблюдателю видимой части поверхности предмета, расположенного между ним и плоскостью проекций.

Основные виды – виды, полученные ортогональным проецированием на основные плоскости проекций. В черчении к трём известным плоскостям проекций добавлены ещё три параллельные им плоскости проекций, которые в совокупности образуют поверхность куба. Изображаемый объект мысленно помещают в центре полого куба таким образом, чтобы максимальное количество его элементов (грани, ребра, конструктивные части) располагались бы параллельно граням куба и, затем, ортогонально проецируют его на внутреннюю поверхность каждой грани (рис. 44).

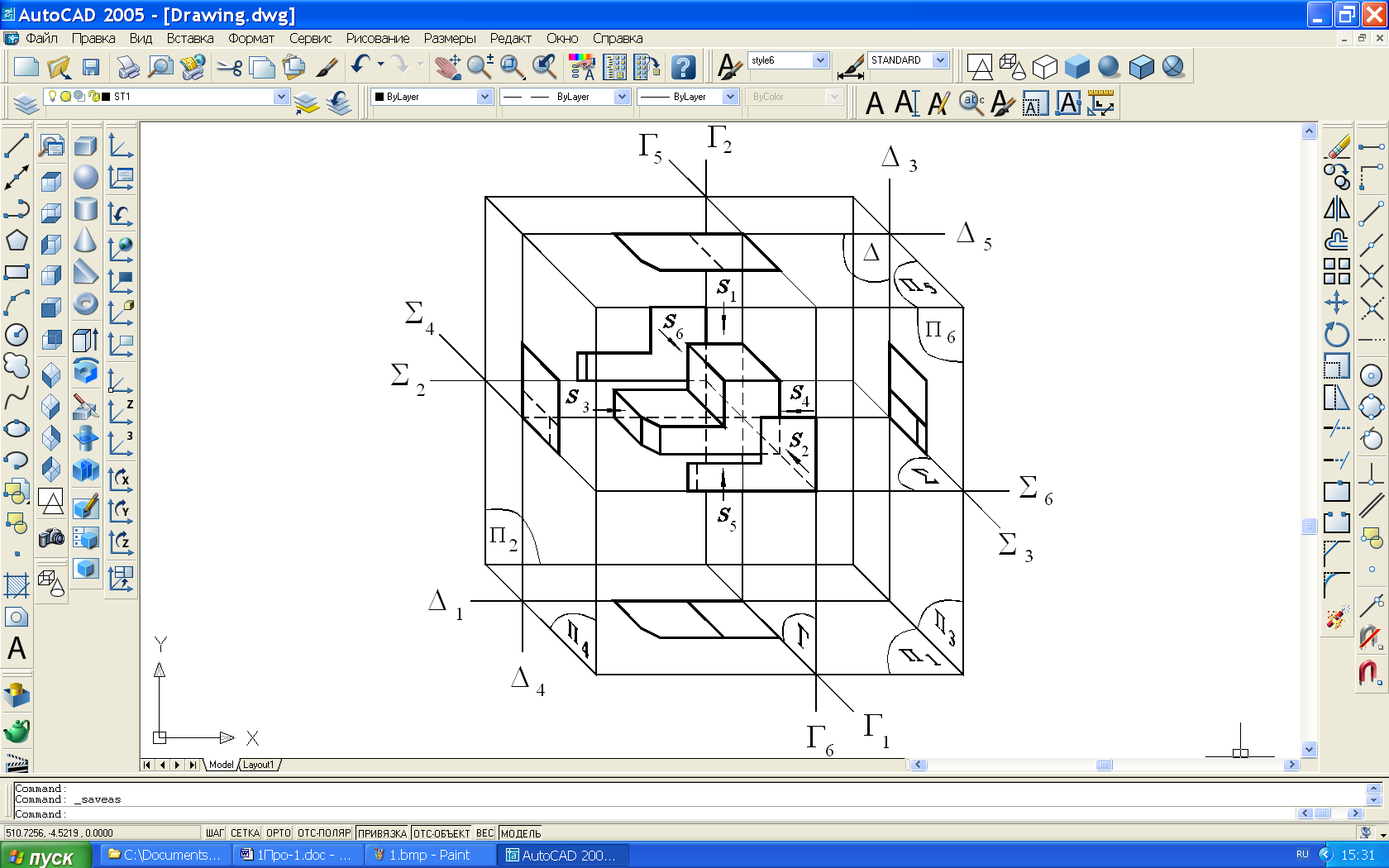
Рис. 44

Названия полученных основных видов соответствуют направлениям проецирования.

Направление проецирования	Основная плоскость	Название основного вида
s1 — сверху П1	П1	вид сверху
s2 — спереди П2	П2	вид спереди (главный вид)
s3 — слева П3	П3	вид слева
s4 — справа П4	П4	вид справа
s5 — снизу П5	П5	вид снизу
s6 — сзади П6	П6	вид сзади

Затем куб ставят гранью П₂ на чертеж, разрезают его по ребрам определенным образом (рис. 45) и совмещают другие его грани с задней гранью П₂ и плоскостью чертежа.

Вид спереди, как правило, является наиболее характерным изображением объекта, поэтому его ещё называют главным видом.

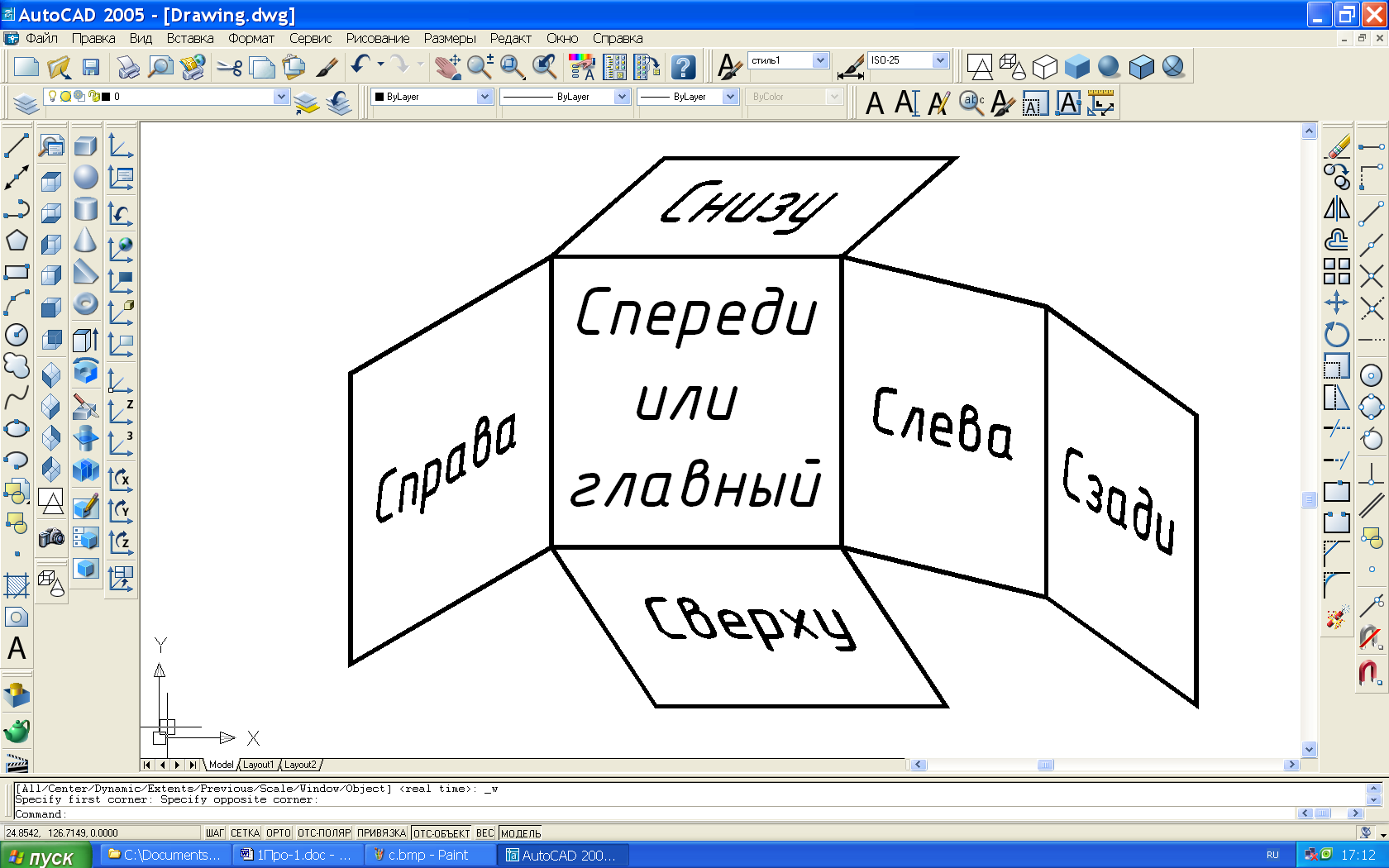
Рис. 45

В качестве ориентира для отсчета размеров объекта при построения его изображений используют три, так называемые базовые плоскости , и . Базовые плоскости проецируются на основные плоскости проекций в виде базовых линий: , , , , ₂ , ₃ , ₄ , ₆ , ₁ , ₂ , ₅ , ₆ (рис. 44, 46).

Изображения располагаются в проекционной связи; названия видов на чертеже не указывают (см. рис. 46). Более подробно построение основных видов см. в [14].

Рис. 46

Следует обратить внимание на зеркальность внешних контуров видов: спереди и сзади, справа и слева, сверху и снизу, связанную с вращением параллельных граней в разные стороны.

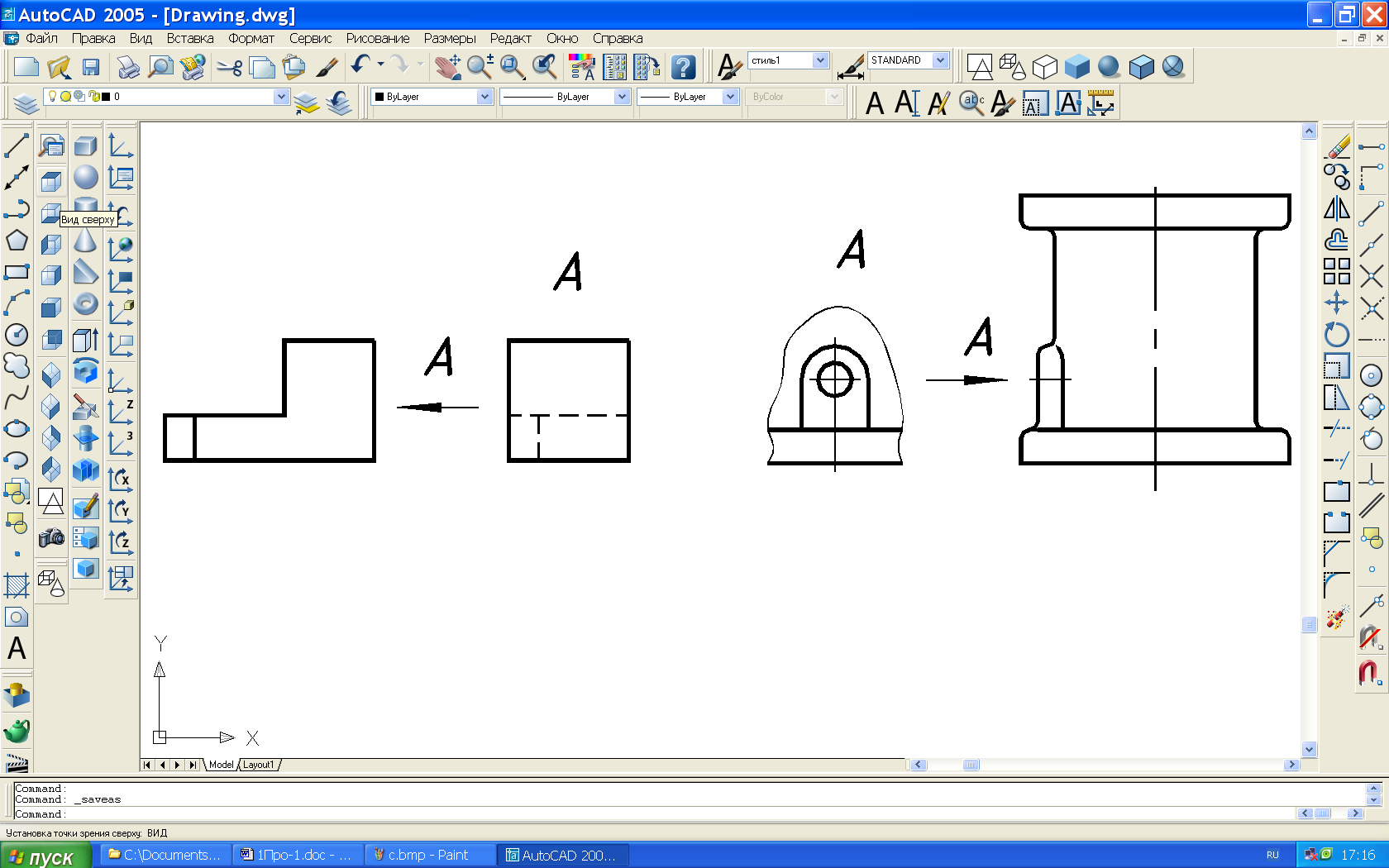
Местный вид – изображение отдельного, ограниченного

места поверхности предмета.

Местный вид ограничивают сплошной волнистой линией,

которая не должна совпадать с другими линиями внутри

контура изображения. На рис. 47 вид слева оформлен как

местный вид.

Рис. 47

Дополнительный вид – изображение предмета на плоскости, непараллельной ни одной из основных плоскостей проекций. Дополнительный вид строят как дополнительную проекцию (методом замены плоскостей проекций) и обозначают прописной буквой кириллицы (рис. 48). У изображения, связанного с дополнительным видом, ставят стрелку, указывающую направления взгляда с таким же обозначением. Подробное построение дополнительного вида см.в [14].

Типовая задача 10 (рис. 48-49): Построить дополнительный вид верхней наклонной грани детали с отверстием.

На чертеже (рис. 49) построение дополнительного вида начинаем с проведения базовых линий Δ₁ и Δ₅, которые всегда перпендикулярны направлениям проецирования или линиям связи. Далее, измеряя удаление ± y любых проекций точек детали, например, М₁, , от ба­зовой линии Δ₁ на основном виде и откладывая их от базовой линии Δ₅ по новым линиям связи, получаем проекции этих точек (М₅, ) на дополнительном виде. Аналогично строим все опорные точки объекта и, соединяя их, получаем дополнительный вид, который обозначаем как « А » (заглавная буква кириллицы). На главном виде стрелкой указываем направление взгляда и обозначаем её такой же буквой.

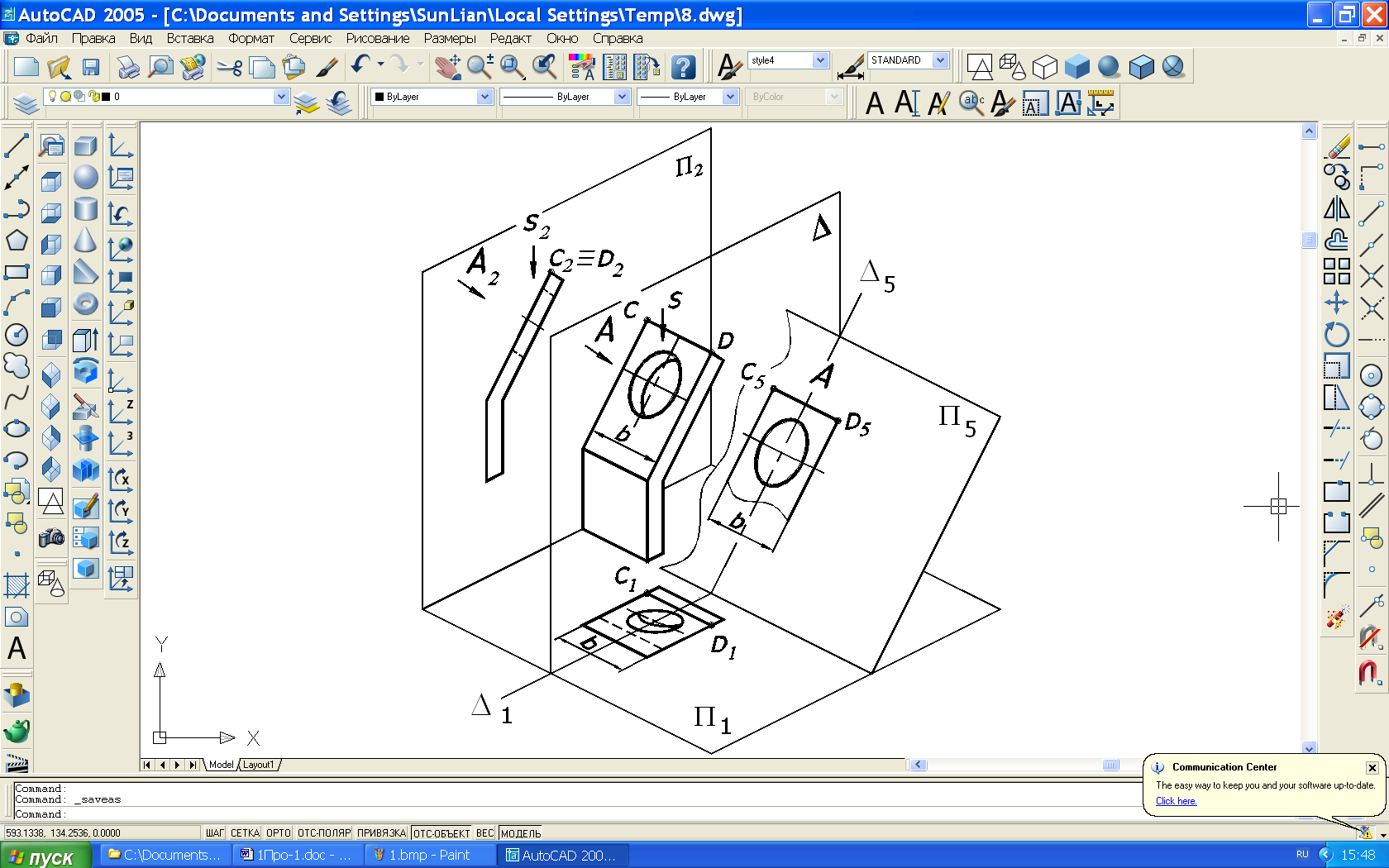
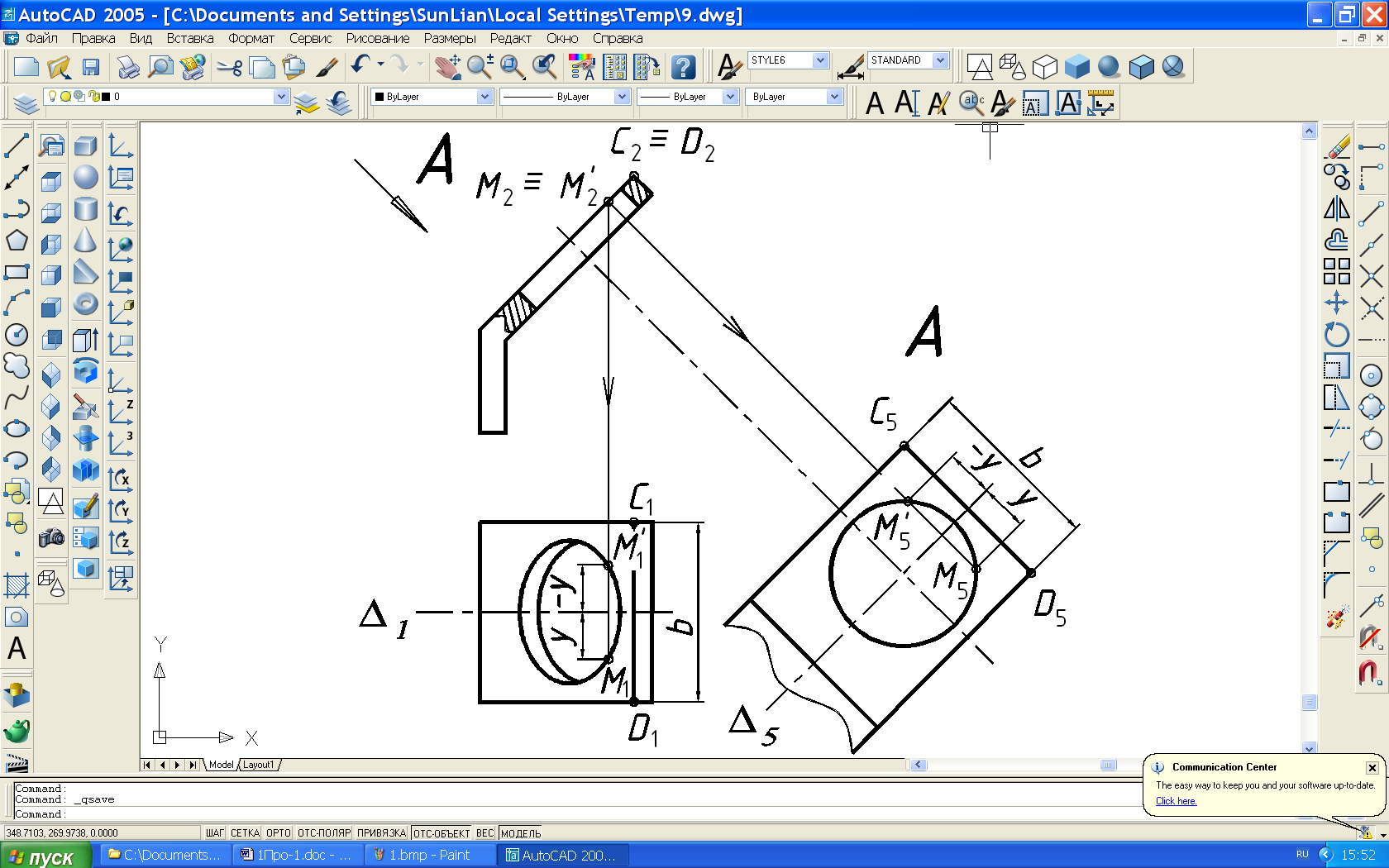
Рис. 38 Рис. 39