3 Описание программного продукта
На основе выбранных алгоритмов в математическом пакете MatLab разработан и реализован программный продукт (ПП), решающий поставленную задачу размещения плоских геометрических объектов на полубесконечной полосе. Данный ПП предназначен для размещения окружностей с помощью метода проекционного градиента.
Исходными данными задачи является радиусы, размещаемых кругов и ширина полосы. В результате работы программы пользователь получает возможность наглядно увидеть лучшее размещение в графическом окне программного продукта.
Работа с программой начинается с запуска математического пакета MatLab. Затем открываем м-файл с основной программой. Для этого выбирается пункт главного меню Файл Открыть. Появляется программный код (рис. 3.1).
В данном файле задаются следующие параметры: ширина полосы и набор радиусов. Кроме того, можно генерировать случайные радиусы окружностей.
После того как заданы данные для размещения, производим запуск программного продукта с помощью Run, и через некоторое время появится графическое окно размещения окружностей на полубесконечной полосе, которое показано на рис. 3.2.
Рисунок 3.1 – Загрузка м-файла с программным кодом
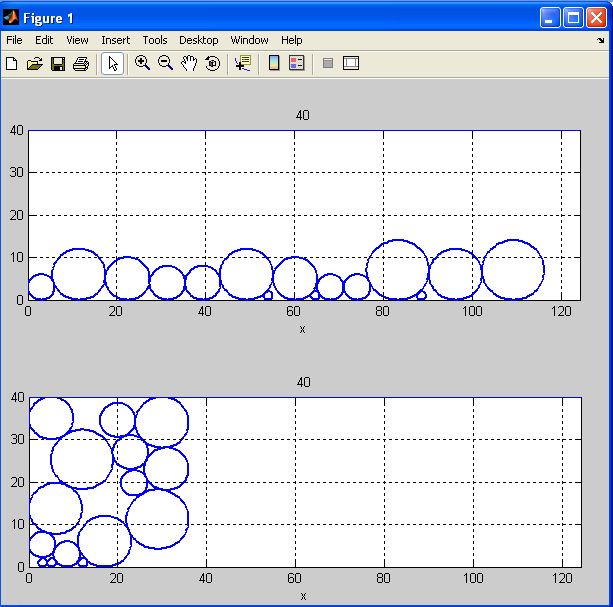
Рисунок 3.2 – Графическое окно программы после выполнения размещения для 15 случайных окружностей
Как видно из рис. 3.2 длина начального размещения – 116.16, ширина полосы - 40, а минимальная длина – 35.96.
Приведем на рис. 3.3 пример размещения для 50 случайных окружностей и ширине полосы – 30.
Рисунок 3.3 – Графическое окно программы после выполнения размещения для 50 случайных окружностей и ширине полосы равной 30
Список использованных источников
А.Фиакко, Г.Мак-Кормик «Нелинейное программирование. Методы последовательной безусловной минимизации», М.:Издательство «Мир», 1972. – 241с.
Мину М. Математическое программирование. Теория и алгоритмы: Пер. с фр. и предисловие А.И.Штерна. – М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 488 с.
Базара М., Шетти К.Нелинейное программирование. Теория и алгоритмы: Пер. с англ. – М.: Издательство «Мир», 1982. – 583с.
Химмельблау Д. «Прикладное нелинейное программирование», М.: Издательство «Мир», 1975. – 536с.
А.В.Аттетков,С.В.Галкин,В.С.Зарубин. Методы оптимизации: Учеб.для вузов /В.С.Зарубина, А.П.Крищенко. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. – 440 с. (Сер. Математика в техническом университете; Вып. XIV).
Харчистов Б.Ф.Методы оптимизации: Учебное пособие. – Таганрог: Изд-во ТРТУ, 2004. – 140с.
http://iasa.org.ua/ru/forstudent/materials.html - учебный материал по дисциплине «Исследование операций» на сайте факультета второго высшего и последипломного образования ННК «ИПСА» НТУ «КПИ»
Барсов С.С., Храпов П.В., Чуев В.Ю. Численные метода поиска экстремума: Методические указания к выполнению лабораторных работ по курсу «Численные методы». – М.: Изд-во МГТУ, 1990. – 35с., ил.
http://mmedia0.cc.rsu.ru/pls/rsuweb/umr.umr_download?p_umr_id=44985 – Сантылова Л.И., Гусаков С.В., Землянухина Л.Н. «Вариационное исчисление и методы оптимизации»: Метод.указания для студентов специальности «Прикладная математика и информатика» - Ростов-на-Дону: мех.-мат. фак. ЮФУ, 2010