Пример выполнения задания для курсового проекта

Постановка задачи: разместить без взаимных пересечений n кругов различных радиусов в полубесконечной полосе так, чтобы длина занятой её части была минимальной.

1. Построение математической модели

1.1 Обозначения и неформальная постановка

Введём необходимые обозначения. Обозначим полубесконечную полосу буквой S. Количество кругов обозначим n, i-й круг – T_i, радиус i-го круга – r_i, . Примем за полюс круга его центр. Границей размещения назовём отрезок на полосе S, после которого не расположено ни одного круга. Расстояние от начала полосы до этого отрезка обозначим Z (рис.1.1).

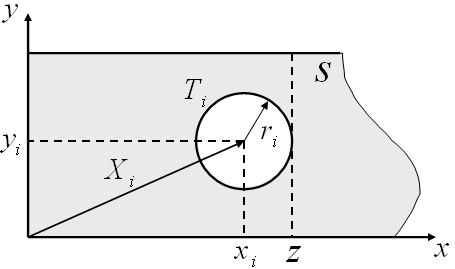
Рисунок 1.1 – Геометрическое представление задачи

Параметрами размещения i-го круга являются координаты его центра (x_i, y_i). Так как они имеют определенный физический смысл, то их можно считать составляющими вектора Х_i.

Задачей является размещение набора кругов так, чтобы длина занимаемой части полосы была минимальной.

Математическая модель содержит область допустимых решений и функцию цели. Обозначим область допустимых решений буквой D.

1.2 Область допустимых решений задачи

Если существует набор векторов Х_i, , такой, который попадает в область допустимых значений D, то задача имеет решение и данный набор векторов является одним из решений.

Область D описывается условиями:

а) круги должны принадлежать полосе (рис. 1.2):

T_i (Х_i) S, . (1.1)

Рисунок 1.2 – Геометрическое представление условия принадлежности кругов полосе

б) круги не должны пересекаться между собой (рис. 1.3):

int T_i(Х_i) ∩ int T_j(Х_j) = 0, ; 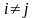. (1.2)

Для формализации условий не пересечения был разработан аппарат Ф-функции [14].

Рисунок 1.3 – Геометрическое представление условия не пересечения пары кругов

1.3 Использование Ф-функций

Ф-функции вводят для каждой пары T_i, T_j размещаемых объектов. При определении и описании их свойств будем учитывать особенности нашей задачи. Зависимость объекта от значения вектора переменных соответствующей геометрической информации будем выражать в виде – 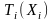. Для нашей задачи .

Любая, всюду определенная и непрерывная функция в , обладающая следующим характеристическим свойством:

, если ;

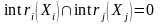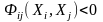, если ,

;

, если ,

называется Ф-функцией [14].

Таким образом, характеристическое свойство – функции позволяет говорить о пересечении, не пересечении и касании соответствующих объектов. Причем условия непересечения для пары размещаемых объектов выполняется тогда и только тогда, когда размещаемые объекты принадлежат области неотрицательных значений соответствующей Ф-функции.

Условия (1.1, 1.2) можно записать в виде Ф-функций. Условие (1.1) эквивалентно выполнению неравенства

,

а условие (1.2) соответствует выполнению неравенства

Таким образом, область допустимых решений задачи описывается с помощью Ф-функций так:

(1.3)

Представим область допустимых решений задачи (1.3) в аналитическом виде.

1.4 Описание Ф_i0 – функции

Представим условие принадлежности кругов полосе в аналитическом виде. Графическое представление показано на рис. 1.2, математическое представление выражено условием T_i (X_i) S, которое эквивалентно системе неравенств (1.4).

(1.4)

Неравенство представляет собой условие непересечения кругов верхней границы, неравенство – нижней, неравенство – левой, неравенство - правой.

Система неравенств (1.4) эквивалентна уравнению системы (1.3)

Систему 1.4 для удобства запишем в виде:

(1.5)

1.5 Описание Ф_ij – функции

Представим условие не пересечения кругов в аналитическом виде. Графическое представление показано на рис.1.3, математическое представление для каждой пары кругов выражено условием , которое эквивалентно неравенству (1.6).

, где (1.6)

Неравенство (1.5) эквивалентно уравнению системы (1.3)

1.6 Математическая модель

Функция цели имеет вид: ,

Или

где , , ,

x_i, y_i – координаты полюса i-го круга.

Исходя из (1.4 – 1.6) область D описывается: