Общая схема метода проекции градиента
Шаг 0. Определение
допустимой точки
.
Шаг 1. Построение .
Шаг 2. Если , то переходим на шаг 6.
Шаг 3. Определяем
,
.
Шаг 4. Если
,
то добавляем ограничение в
.
Шаг 5.
,
.
Переходим на шаг 1.
Шаг 6. Определение , решение системы Куна-Таккера.
Шаг 7. Если , то – решение задачи. Остановка алгоритма. Иначе – удаление ограничений из и переход на шаг 1.
Пример
Задана функция
с ограничениями
.
Выполнить один шаг методом проекции градиента.
Решение
1. В качестве допустимойточки возьмём
.
2. В данной точке
активными являются лишь ограничения
неотрицательности параметров
и
.
Тогда
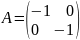
и в соответствие с (3.6) имеем:
.
Так как
– нулевая матрица, то из (3.5) видно, что
.
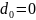3. Определим λ как решение системы Куна-Таккера:
;
;
.
Удалим из матрицы
ту строку, индексы которой соответствует
максимальное по модулю значение
.
Тогда получим
новую матрицу
,
для которой
,
.
Имеем
4. Для определения
найдем минимум функции
.
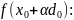
Для определения
максимальной длины шага
рассчитаем
,
где
– ограничения, не входящие в рабочий
список:
;
;
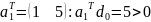и выберем минимальное из двух значений:
;
.
Получили, что
.
5. Переходим на шаг 1 для новой допустимой точки:
.
Метод возможных направлений (метод зойтендейка)
Для каждой
допустимой точки
в
может существовать множество различных
допустимых направлений. Сущность
методов допустимых направлений сводится
к следующему: поиск начинается в
допустимой точке пространства решений
и реализуется по траектории, обеспечивающей
улучшение значений целевой функции и
вместе с тем никогда не выходящей за
пределы допустимой области. В этом
смысле предложенный Розеном метод
проекции градиента представляет собой
одну из модификаций метода допустимых
направлений. Однако необходимо обратить
внимание на следующее: проекция градиента
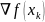на подмножество ограничений, содержащее
,
задает направление поиска, соответствующее
направлению наискорейшего спуска для
целевой функции, тогда как в методе
Зойтендейка используется метрика,
определяемая соотношением
.
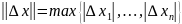Данная метрика приводит к тому, что в качестве допустимого выбирается направление, которое обеспечивает наибольшую минимизирующую поправку к значению целевой функции без нарушения какого-либо из ограничений.
Метод Зойтендейка позволяет оперировать как с линейными, так и с нелинейными ограничениями; однако с его помощью не удается решать задачи с ограничениями в виде равенств.
Рассмотрим задачу вида (2.1)-(2.2). Линеаризация фигурирующих в этой задаче функций путем их разложения в ряд Тейлора в окрестности точки приводит к следующей задаче:
при ограничениях
|
|
(4.1) |
.Процедура Зойтендейка устанавливает наиболее благоприятные из возможных направлений поиска при отправной точке путем решения некоторой подзадачи, структура которой указана ниже.
Перемещение из точки в точку задаетсясоотношением
.
Подстановка в задаче (4.1) вместо вектора его текущего значения приводит к задаче
при ограничениях
|
|
(4.2) |
.
Поскольку
и
являются константами, то необходимые
и достаточные условия реализации
перемещения из точки
в точку
в связи с решением задачи (4.2) имеют
следующий вид:
|
|
(4.3) |
|
и
|
(4.4) |
Любой вектор , удовлетворяющий неравенствам (4.3) и (4.4), одновременно является вектором допустимого направления.
Метод Зойтендейка
выделяет допустимое направление,
обеспечивающее получение наибольшей
минимизирующей поправки к значению
целевой функции
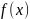на шаге от точки
к точке
путём решения следующей задачи линейного
программирования:
|
|
(4.5) |
при условиях
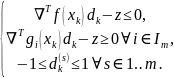
Решая задачу (4.5), определяются составляющие вектора допустимого направления, вдоль которого следует перемещаться из точки в точку .
Алгоритм метода возможных направлений
Шаг 1. Пусть – некоторая допустимая точка задачи (2.1)-(2.2) с ограничениями в виде неравенств.
Шаг 2. Вычисляются
градиенты функции
и
в точке
,
и решается задача (4.5), в результате чего
находится допустимое направление
.
Решение задачи (4.5) находится с помощью
любого из алгоритмов линейного
программирования.
Шаг 3. Если , то определяется максимальная длина шага , осуществляемого в направлении без выхода за пределы допустимой области задачи (1.1)-(1.2):
.
Затем определяется :
.
Новая точка определяется как . Теперь возвращаются к шагу 2 с тем, чтобы начать оптимизационный поиск на (k + 1)-м этапе вычислительного процесса.
Шаг 4. Если
,
поиск решений заканчивается, так как
дальнейшее уменьшение значения
не представляется возможным.
Пример.
Задана функция
с ограничениями
.
Выполнить один шаг методом возможных направлений.
Решение.
1. В качестве допустимойточки возьмём
.
2. Вычислим градиенты функции и в точке :
,
.
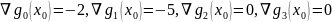В данной точке активными являются лишь ограничения неотрицательности параметров и . Тогда
.
Решив задачу
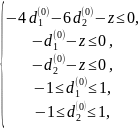
симплекс-методом,
получаем
.
Для определения максимальной длины шага рассчитаем , где – ограничения, не входящие в рабочий список:
,
и выберем минимальное из двух значений:
,
.
Получили, что
.
Тогда
.
Переходим на шаг 2 для новой допустимой точки:
.
Программную реализацию решения данной задачи можно увидеть на рис.4.1.