1. Выбор направления

В методе проекций градиента направление выбирается следующим образом:

1. Если текущая точка является внутренней области , то в качестве направления берется антиградиент.

2. Если текущая точка является граничной, то в качестве направления берется проекция антиградиента на линейное многообразие, порождаемое множеством активных ограничений, точнее, множеством ограничений, входящих в рабочий список.

Необходимо учитывать два условия:

а) значение функции цели должно уменьшаться;

б) направление не должно выводить из области решений.

Направлением выбирается точка, ограничения которой являются активными в точке и должны оставаться активными и в следующей точке , то есть при выборе направления должны выполняться следующие условия:

;

.

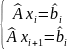Отсюда можем определить, что:

;

;

.

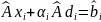(3.4)

Теорема 3.1. Решением задачи поиска минимальной функции при ограничении ( ) является вектор

, где

	;	(3.5)
	.	(3.6)

– матрица проектирования, которая проектирует направление аргумента на линейные многообразия порождаемые векторами набора активных ограничений.

Для того чтобы убедиться в том, что полученные направления удовлетворяют условию (3.4), достаточно умножить матрицу на матрицу проектирования:

.

2. Определение длины шага на каждой итерации.

Вначале найдем для текущей точки и направления максимальную длину шага, при котором мы будем оставаться внутри области допустимых решений. Для этого в новой точке должны выполняться все ограничения вида (2.2). При этом все ограничения рабочего списка в новой точке будут выполняться как строки и равенства, поэтому проверять следует только ограничения, которые не входя в рабочий список.

,

,

,

,

.

(3.7)

Так как точка 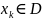, то в этой точке будут выполняться все ограничения вида (2.2).

Рассмотрим две ситуации, которые будут возникать при анализе формулы (3.7):

1.

В этом случае при любом значении ограничение (3.7) будет выполняться.

2.

,

,

,

(3.8)

Для того чтобы новая точка была допустимой необходимо, чтобы условие (3.8) выполнялось для всех ограничений. Тогда максимальная длина шага в направлении может быть получена из формулы:

,

.

(3.9)

3. Критерий оптимальности

Итерационная процедура вида (3.3) будет продолжаться до тех пор, пока в некоторой текущей точке не будут выполняться условия Куна-Таккера, которые будут проверяться только в том случае, если на текущем шаге вектор направления движения

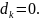
4. Изменение рабочего списка

Добавление ограничений в рабочий список. Если на некоторой итерации длина шага определяется формулой (3.9) совпадает со значением максимальной длины шага, то значит, что еще одно ограничение становится активным и это ограничение добавляется в рабочий список и в матрицу .

Удаление ограничений из рабочего списка. Если на некотором шаге значение вектора , то в текущей точке проверяется выполнение условий Куна-Таккера, то есть решается следующая задача относительно вектора :

.

Если , то это оптимальная точка.

Если , то выбирается один из них обычно максимальный по модулю и соответствующая строка удаляется из .
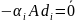
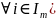